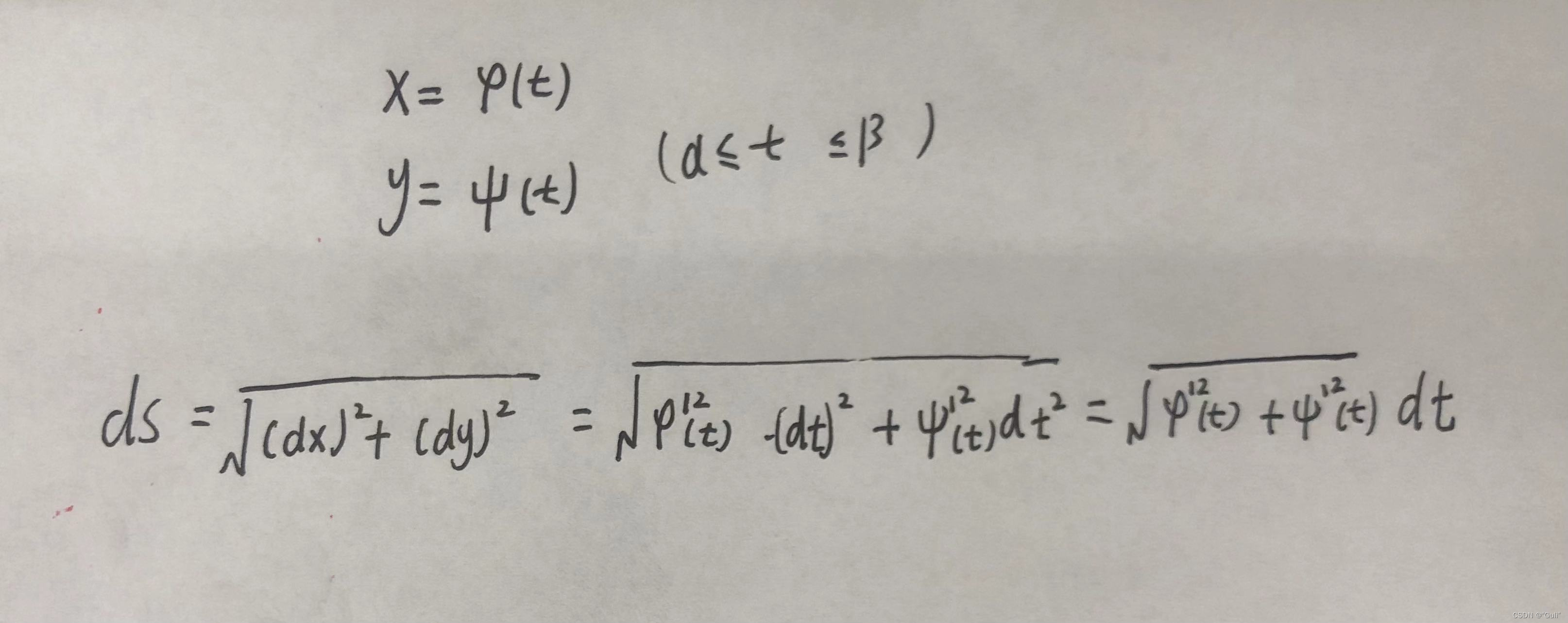目录
前提知识
考题类型:平面图形面积、旋转体体积、旋转体侧面积、平面曲线弧长
两种坐标:极坐标和直角坐标系
求解思路:
注意:
1:平面图形的面积:
常见模型:
面积元素的两种表达:积分区间由x范围确定,积分区间由y范围确定。
典型案例:
1:参数方程求面积:摆线的面积
2:极坐标方程求面积:心形线围成的面积
2:旋转体体积
前提:
求解思路:当y=f(x),绕x轴旋转
旋转体为什么可以用定积分解决?
结论:
3:旋转体的侧面积
弧长公式:
面积元素
所以有:dA = 2 Π* |f(x)| * \sqrt[]{(1 + f'^2(x))}dx
4:平面曲线的弧长
弧长元素: dS = 根号下(1 + y‘2)
极坐标下求弧长:
结论: ds = \sqrt[]{ρ^2(θ)+ρ' ^2(θ)}dθ
参数方程求弧长:
前提知识
考题类型:平面图形面积、旋转体体积、旋转体侧面积、平面曲线弧长
三种不同表达曲线的方法:极坐标和直角坐标系,参数方程
求解思路:
既然是定积分的应用:就应该从定积分定义来解析:分割、替换、求和、取极限
分割:找到积分区间,也就是找到积分上下限的范围,根据不同的题目会有不同的范围取值。
替换:当求面积(或体积)时,应该找出其对应的面积元素(体积元素)
求和:将这些小面积求和
取极限:将分割的区间中的积分范围的最大范围趋于0(这是没有等分的情况下)。
如果是等分的情况下,让n趋于无穷,则每一份小面积的积分范围也趋于0
注意:
1:这里的面积元素(体积元素)指的是,将原来要求的大的面积更换为分割成n份的小面积的一个代表。
2:替换过程中:平面图形面积、旋转体体积这两类题目求元素比较简单。
旋转体侧面积、平面曲线弧长这两类元素替换稍微复杂。
3:在实际求解过程中,求和和取极限一般直接都不怎么重视,因为我们直接把替换好的面积元素加上积分号和积分的上下限范围就是相同的效果
1:平面图形的面积:
常见模型:
面积元素的两种表达:积分区间由x范围确定,积分区间由y范围确定。
如何选择需要根据题目所给信息,去判断使用x或y来做积分区域时求解更加简单来判断。

典型案例:
1:参数方程求面积:摆线的面积
参数方程 x = a(t-sint) , y =a(1-cost),(a>0,0<=t<=2pi)
根据参数方程的面积元素:dA = |y * x 't|dt
面积 A = 3Π * a2
2:极坐标方程求面积:心形线围成的面积
极坐标方程 ρ = a(1 + cosθ)(a>0)
根据极坐标方程的面积元素:dA = \frac{1}{2} * (a(1 + cosθ))2
心型线面积: A = \frac{3}{2} Π * a2
注:记住两个特殊案例的方程以及面积,当题目没有说明曲线的类型也能轻松判断,这个需要背诵。
2:旋转体体积
前提:
1:旋转体体积,如果从学习角度来说,跟随老师学习,并且通过例题的一步一步的推导,不难发现定积分确确实实(一次积分)就能来求旋转体体积。
但是从记忆角度大家,特别是学完二重积分,总会觉得与体积相关的求解都是二重积分的范畴,从而引起混乱
2:圆柱体的体积公式: Π * r2 * h
求解思路:当y=f(x),绕x轴旋转
分割:将积分区间分割成n份,这里的积分区间就是x的范围。
替代:用f(x)替代圆柱体的半径r,且x∈Δx,从而构造一个体积元素 (由于圆柱体体积公式可推出) Π * f2(x) dx = Π * r2 dx。= dV
求和;
取极限;
通过求解思路得到:
V = ∫ab dV = ∫ab Π * f2(x) dx
旋转体为什么可以用定积分解决?
因为旋转体的被积函数 Π * f2(x) 仅仅是关于x的函数。所以我们只需要对x进行积分就能得到我们所需要的体积。
结论:
我们无法从所求物理量中去直接判断用定积分还是二重积分,可以所求物理量的特征(特征元素的表达)去判断去选择使用定积分还是二重积分。打破固化思维。
因此我们可以通过判断被积分的函数自变量的个数来确定是用定积分还是二重积分来进行计算我们所求的物理量。
3:旋转体的侧面积
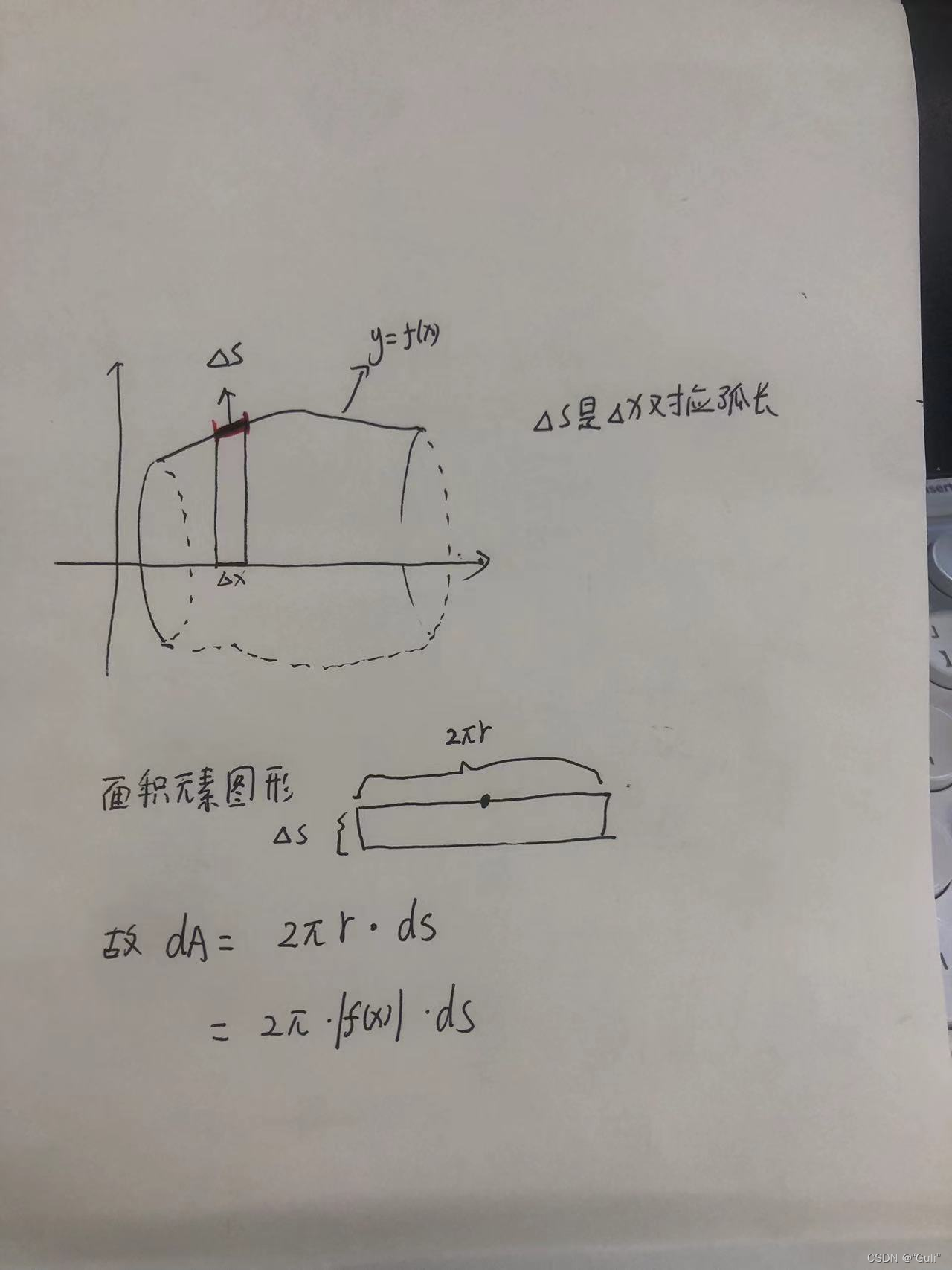
当求解旋转体的侧面积时,我们需要注意所求物理量的特征:我们不能再以直代曲,而是用弧长表示。
对与 y=f(x),绕x轴旋转后所形成圆柱体的表面积的面积元素dA:
dA = 2 Π |f(x)| dS : 2 Π |f(x)| 表示面积元素的长,dS 弧长(f(x)中每个Δx对应弧长)

弧长公式:
dS = \sqrt[]{(1 + f'^2(x))}dx (第四个平面曲线的弧长相同,都是取曲线上切线的对应的一小段做弧长)
面积元素
所以有:dA = 2 Π* |f(x)| * \sqrt[]{(1 + f'^2(x))}dx
4:平面曲线的弧长
关注点在于:如何替换:
我们用(x,f(x))处的切线上对应的一小段长度近似等于弧长,而切线上一小段长度。
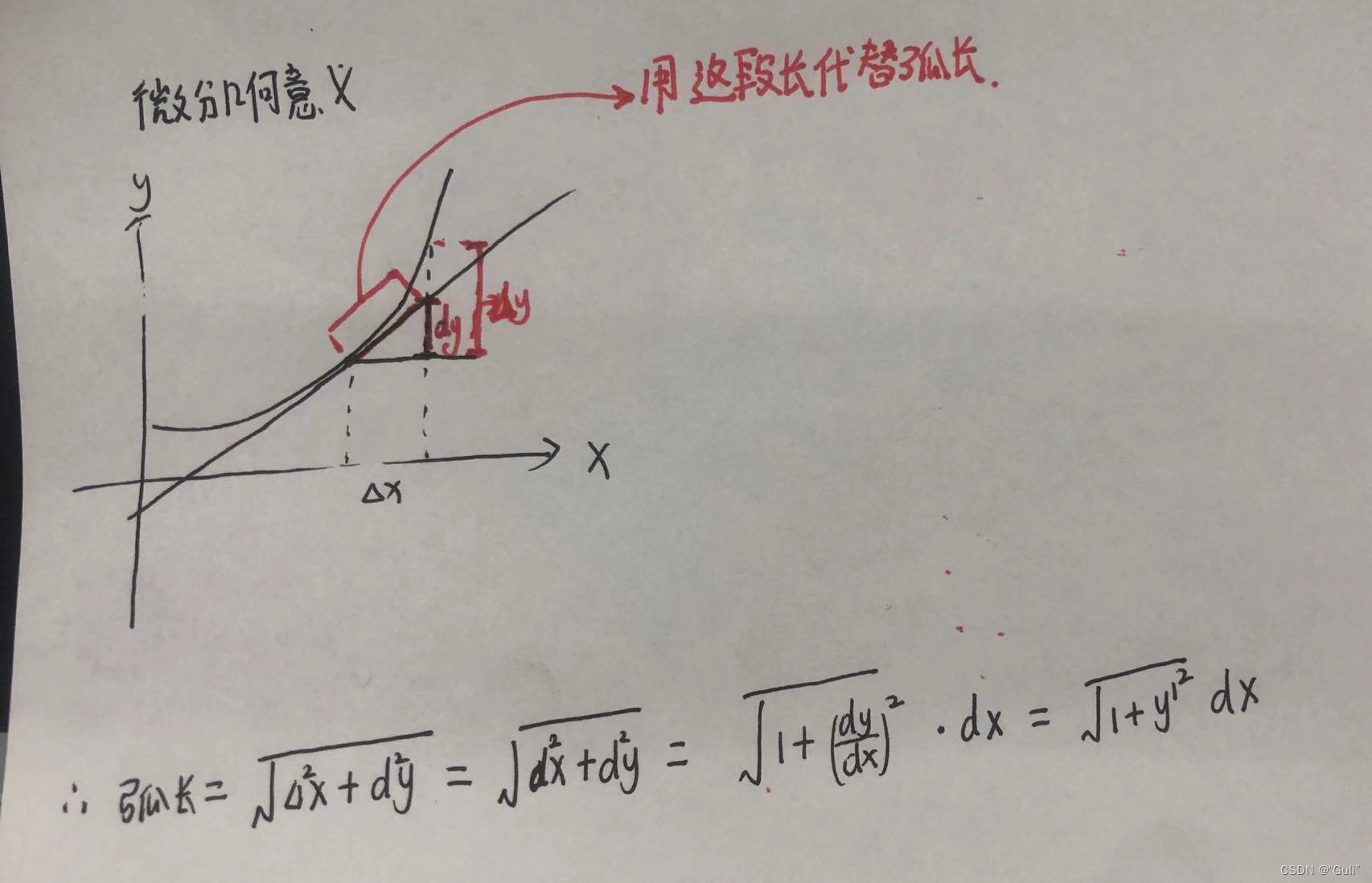
弧长元素: dS = 根号下(1 + y‘2)
极坐标下求弧长:
ρ = ρ(θ) (α <= θ <= β)
解题步骤:将极坐标方程参数方程化:然后求弧长元素,然后在θ上积分。
结论: ds = \sqrt[]{ρ^2(θ)+ρ' ^2(θ)}dθ
参数方程求弧长:
参数方程: