#机器学习 #深度学习 #基础知识 #特征工程 #数据编码
背景
在现实生活中,我们面对的数据类型有很多,其中有的数据天然为数值类型具备数值意义,那么可以很自然地和算法结合,但是大部分数据他没有天然的数值意义,那么将他们送入到算法前,就需要对数据进行编码处理,将其转换为数值类型,才可以送入算法进行运算.
问题
处理一个这样算法问题时,首先我们需要确认所处理的数据是什么类型的,是否可以直接输入模型,如果不能,那么我们需要根据数据本身的特点,然后结合算法的适配的格式,去对数据进行编码处理.因此,我们需要依次思考以下的几个问题:
- 常见的类别数据有哪些形式?其中有哪些是需要进行编码的?
- 哪些算法能接收未经编码的类别型特征?哪些算法不能?
- 常见的编码类型及其优缺点?如何选择适合的编码方式?
解决方案
常见的类别特征有哪些?其中有哪些是需要进行编码的?
类别型特征是指在数据集中表示某种类别或属性的特征。它包含有限个离散的取值,通常用于描述无序的分类或标签信息。类别型特征没有固定的数值间隔和数值运算意义,只表示不同类别之间的区别和关系。
例如,性别、颜色、地区、职业、喜好程度、股票种类、专业等都可以是类别型特征。性别可以有两个取值:男和女;颜色可以有多个取值:红、蓝、绿等;地区可以有多个取值:东、南、西、北等;职业可以有多个取值:医生、教师、工程师等;问卷调查中,对一件事的喜好程度分为厌恶、无感、较喜欢、喜欢、特别喜欢等;股票可以分为煤炭,光伏,消费,白酒,医疗等等不同的板块;高考报志愿时,专业可以分为计算机科学,基础物理学,临床医学,兽医学,法律,文学等等.
总结来看,这些类别特征按照是否有序可以分为: 有序类别特征(Ordinal Categorical Features)是指类别之间存在自然顺序或等级关系的特征。这类特征的值可以进行排序,但不能直接进行数值运算;无序类别特征(Nominal Categorical Features)是指类别之间没有自然顺序或等级关系的特征。这类特征的值只是表示不同的类别,不存在排序关系。要是按照类别的数量来来分:高基类类别特征,具有大量唯一值的类别,特征类别总数很大;低基类类别特征,具有少量唯一值的类别,特征类别总数较少.
关于哪些类别特征需要编码,这个问题其实需要结合所采用的算法统筹考虑才有实际意义.但是,单从类别特征的分类上来考虑,可以划分为四种类型,它们的编码难点可以总结为下:
| 有序 | 无序 | |
| 低基类 | 保留类别顺序关系,保证类别均衡 | 保证类别间独立,保证类别均衡 |
| 高基类 | 保留类别关系,防止过拟合,解决稀疏性 | 保证类别间独立,解决稀疏性 |
哪些算法能接收未经编码的类别特征?哪些算法不能?
首先,没有经过编码的数据大多数为字符串类型.不同的算法所接受的数据格式是不同的,所以根据具体算法接收的数据格式来看.一般来说,只有能够直接依据类别划分就能进行运行的算法可以不用进行编码,决策树类算法(决策树,随机森林),规则基础算法(C5.0)以及基于统计概率的部分贝叶斯分类算法,其余的算法都需要对类别型特征进行编码处理后才能让算法正常运行.
常见的编码类型及其优缺点?如何选择适合的编码方式?
标签编码
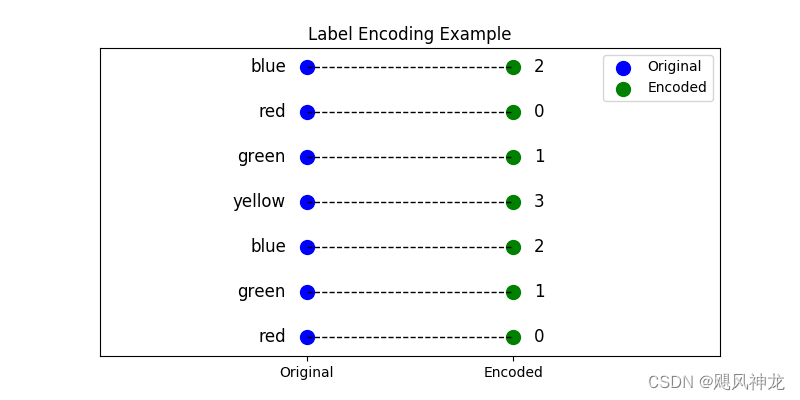
不适用于高基类类别特征,并且编码后的自然数对于回归任务来说是线性不可分的,即自然数之间的关系不能代表编码前的类别关系.
哈稀编码
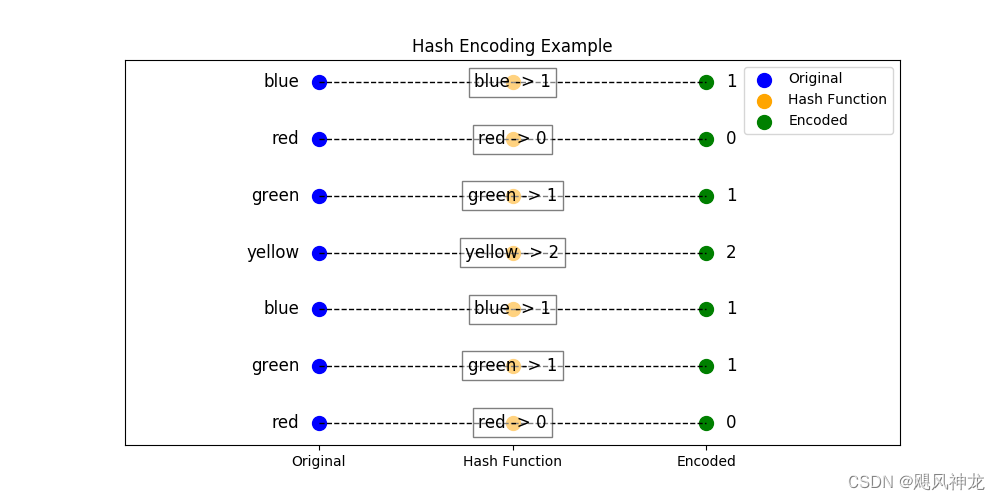
将类别特征通过哈希函数映射到固定数量的哈希桶中。这种方法在类别数量非常多时可以减小维度,但可能引入哈希冲突。
独热编码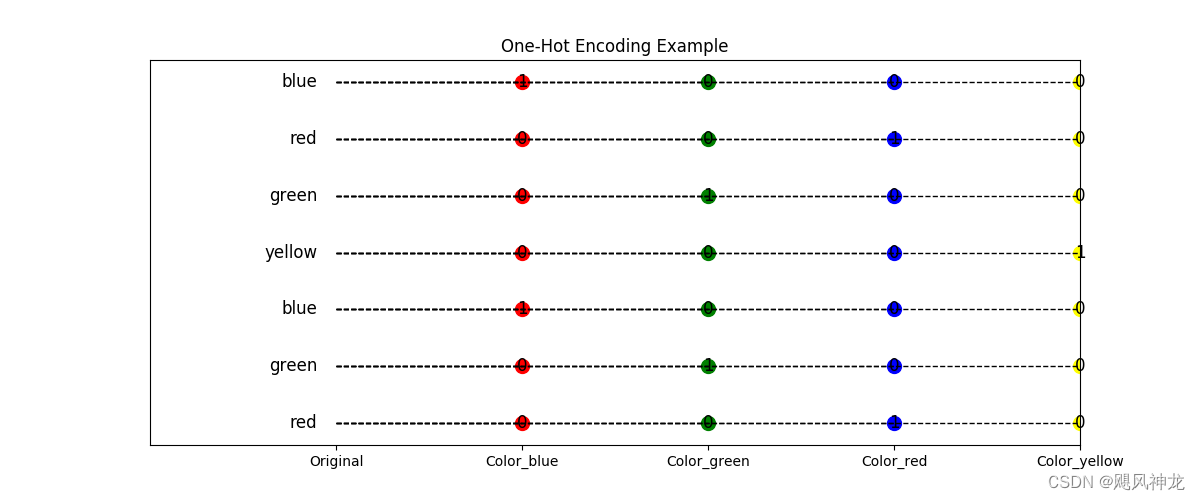
独热编码(One-Hot Encoding),又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都有它独立的寄存器位,并且在任意时候,其中只有一位有效。这个方法能很好的保证编码后,各个类别特征的独立性,但是面对高基类类型特征时,会比较稀疏从而浪费资源.
计数编码
计数编码(Count Encoding,也称频率编码)的过程,可以按照以下步骤进行:
- 原始类别数据:列出原始的类别数据。
- 计算类别频数:计算每个类别在数据集中出现的频数。
- 替换类别值:用类别的频数替换原始的类别值。
假设我们有一个类别特征 "Color",它有以下类别值:红色、绿色、蓝色、黄色、绿色、红色、蓝色。我们将计算这些颜色频数得:红色:2,绿色:2,蓝色:2,黄色:1。这种编码方式的问题显而易见,编码只关注了类别在数据集中出现的频次,但是忽略了类别本身的意义.所以,这种方式可能只适用于模型不关心类别意义,而关注类别统计属性的模型中.
直方图编码

实际上直方图编码,也是基于统计的编码,只不过它统计的不是单纯类别样本出现的次数,而是某一种特征在不同类别中的出现频次.这样我们通过先验的统计这些每个类别中这些特征的频次,然后观察样本中表现出的特征,来预测这个样本的类别.直方图编码能清晰看出特征下不同类别对不同预测标签的贡献度,缺点在于:使用了标签数据,若训练集和测试集的类别特征分布不一致,那么编码结果容易引发过拟合。此外,直方图编码出的特征数量是分类标签的类别数量,若标签类别很多,可能会给训练带来空间和时间上的负担。
WOE编码
权重证据编码(Weight of Evidence Encoding, WOE)的过程,我们可以按照以下步骤进行:
- 原始类别数据:列出原始的类别数据和目标变量。
- 计算类别的WOE值:计算每个类别的WOE值。
- 替换类别值:用类别的WOE值替换原始的类别值。
假设我们有一个类别特征 "Color",它有以下类别值:红色、绿色、蓝色、黄色,并且有一个二进制目标变量 "Target"。
权重证据(WOE)的计算公式为:
其中,"Good" 和 "Bad" 通常是正类和负类的计数。
我们需要计算每个类别的Good和Bad的分布:
- 红色:Good = 1,Bad = 1
- 绿色:Good = 1,Bad = 1
- 蓝色:Good = 1,Bad = 1
- 黄色:Good = 0,Bad = 1
总的Good和Bad数量:
- Total Good = 3
- Total Bad = 4
计算WOE值:
- 红色:
- 绿色:
- 蓝色:
- 黄色:
(注意:在实际应用中我们会处理这种情况)
透过公式,我们可以把WOE理解成:每个分组内坏客户分布相对于优质客户分布之间的差异性。
WOE存在几个问题:
- 分母可能为0.
- 没有考虑不同类别数量的大小带来的影响,可能某类数量多,但最后计算出的WOE跟某样本数量少的类别的WOE一样。
- 只针对二分类问题。
- 训练集和测试集可能存在WOE编码差异(通病)。
对于问题1,可加入regularization(默认值为1)。

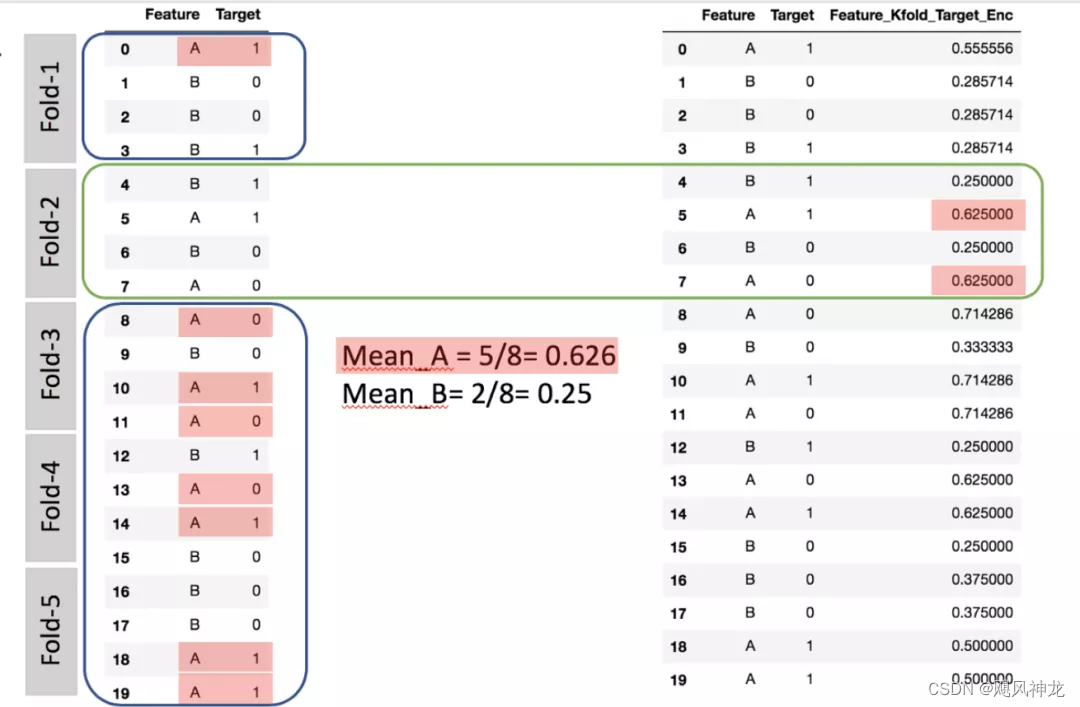
目标编码
亦称均值编码(mean encoding)、似然编码(likelihood encoding)、效应编码(impact encoding),是一种能够对高基数(high cardinality)自变量进行编码的方法 (Micci-Barreca 2001) 。如果某一个特征是定性的(categorical),而这个特征的可能值非常多(高基数),那么目标编码(Target encoding)是一种高效的编码方式。在实际应用中,这类特征工程能极大提升模型的性能。 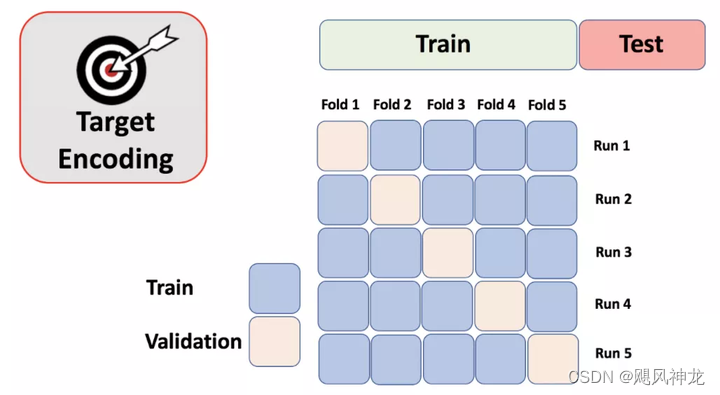
模型编码
其实模型编码思想很简单,即用神经网络来将输入的数据映射到一个易于算法进行的空间中.这也是很多预训练模型能够有利于实际任务的原因.但是,其中的优点与缺点也十分明显,优点是利用深度学将远特征映射到更有剖利于算法施行的空间中,缺点是需要大量数据做预训练,以及使用深度学习模型会可能有较大的资源消耗.
代码实践
标签编码
Scikit-learn中的LabelEncoder是用来对分类型特征值进行编码,即对不连续的数值或文本进行编码。其中包含以下常用方法:
- fit(y) :fit可看做一本空字典,y可看作要塞到字典中的词。
- fit_transform(y):相当于先进行fit再进行transform,即把y塞到字典中去以后再进行transform得到索引值。
- inverse_transform(y):根据索引值y获得原始数据。
- transform(y) :将y转变成索引值。
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
city_list = ["red", "green", "blue", "red"]
le.fit(city_list)
print(le.classes_) # 输出为:['blue' 'green' 'red']
city_list_le = le.transform(city_list) # 进行Encode
print(city_list_le) # 输出为:[2 1 0 2]
city_list_new = le.inverse_transform(city_list_le) # 进行decode
print(city_list_new) # 输出为:['red' 'green' 'blue' 'red']哈稀编码
可以自由的定义hash函数,原则上不要产生过多碰撞就行,其中依据什么来hash可以结合具体情况选择,以便编码后的特征有利于算法的进行
import pandas as pd
import numpy as np
# 原始数据
data = {
'类别特征': ['Apple', 'Banana', 'Orange', 'Banana', 'Apple', 'Orange', 'Grape', 'Apple']
}
df = pd.DataFrame(data)
# 选择哈希桶数量
num_buckets = 4
# 定义哈希编码函数
def hash_encode(value, num_buckets):
return hash(value) % num_buckets
# 应用哈希编码函数
df['哈希值'] = df['类别特征'].apply(lambda x: hash_encode(x, num_buckets))
# 独热编码哈希值
hash_encoded = pd.get_dummies(df['哈希值'], prefix='哈希桶')
# 将哈希编码结果合并到原始数据中
result_df = pd.concat([df, hash_encoded], axis=1)
# 打印结果
print(result_df)独热编码
LabelBinarizer:将对应的数据转换为二进制型,类似于onehot编码,这里有几点不同:
- 可以处理数值型和类别型数据
- 输入必须为1D数组
- 可以自己设置正类和父类的表示方式
from sklearn.preprocessing import LabelBinarizer
lb = LabelBinarizer()
city_list = ["red", "blue", "green", "blue"]
lb.fit(city_list)
print(lb.classes_) # 输出为:['blue' 'green' 'red']
city_list_le = lb.transform(city_list) # 进行Encode
print(city_list_le)
# 输出为:
# [[0 0 1]
# [1 0 0]
# [0 1 0]
# [1 0 0]]计数编码
import pandas as pd
# 原始数据
data = {
'类别特征': ['Apple', 'Banana', 'Orange', 'Banana', 'Apple', 'Orange', 'Grape', 'Apple']
}
df = pd.DataFrame(data)
# 计算每个类别的频数
frequency_encoding = df['类别特征'].value_counts()
# 应用频数编码
df['频数编码'] = df['类别特征'].map(frequency_encoding)
# 打印结果
print(df)
直方图编码
计数编码是统计单纯特征数量,直方图编码是统计特征在不同类别中的分布.
import pandas as pd
# 原始数据
data = {
'类别特征': ['A', 'A', 'B', 'B', 'A', 'A', 'B'],
'目标变量': [0, 1, 0, 1, 2, 2, 2]
}
df = pd.DataFrame(data)
# 计算每个类别特征在目标变量各个取值上的分布
histogram_encoding = df.groupby('类别特征')['目标变量'].value_counts(normalize=True).unstack(fill_value=0)
# 为了便于合并,将列名转换为字符串
histogram_encoding.columns = [f'目标变量_{col}' for col in histogram_encoding.columns]
# 合并编码结果到原始数据
df = df.join(histogram_encoding, on='类别特征')
# 打印结果
print(df)WOE编码
WOE值的计算公式为:
WOE=ln(正样本比例负样本比例)WOE=ln(负样本比例正样本比例)
其中:
- 正样本比例(Positive Rate):该类别在正样本中的占比。
- 负样本比例(Negative Rate):该类别在负样本中的占比。
import pandas as pd
import numpy as np
# 原始数据
data = {
'类别特征': ['A', 'A', 'B', 'B', 'A', 'A', 'B', 'A'],
'目标变量': [0, 1, 0, 1, 1, 0, 1, 0]
}
df = pd.DataFrame(data)
# 计算每个类别的正负样本数量
total_positive = df['目标变量'].sum()
total_negative = len(df) - total_positive
# 计算每个类别的正负样本数量
positive_count = df[df['目标变量'] == 1].groupby('类别特征').size()
negative_count = df[df['目标变量'] == 0].groupby('类别特征').size()
# 计算每个类别的正负样本比例
positive_ratio = positive_count / total_positive
negative_ratio = negative_count / total_negative
# 填充缺失值为0
positive_ratio = positive_ratio.fillna(0)
negative_ratio = negative_ratio.fillna(0)
# 计算WOE值
woe = np.log(positive_ratio / negative_ratio)
# 打印每个类别的WOE值
print(woe)
# 应用WOE编码
df['WOE编码'] = df['类别特征'].map(woe)
# 打印结果
print(df)
目标编码
根据属性与类别的分布统计,用似然函数进行编码
import pandas as pd
# 原始数据
data = {
'类别特征': ['A', 'B', 'A', 'B', 'A', 'C', 'B', 'C', 'A', 'B'],
'目标变量': [1, 0, 1, 1, 0, 0, 1, 0, 1, 1]
}
df = pd.DataFrame(data)
# 计算每个类别的目标变量均值
target_mean = df.groupby('类别特征')['目标变量'].mean()
# 打印每个类别的目标变量均值
print("目标变量均值:\n", target_mean)
# 应用目标编码
df['目标编码'] = df['类别特征'].map(target_mean)
# 打印结果
print("\n目标编码结果:\n", df)
模型编码
在各个领域中的backbone预训练模型,以及当下在大模型领域广泛运用的CLIP.
总结
处理类别型编码时,需要综合考虑数据本身的特性:数据量,类别量,样本的分布特性,样本属性重要程度;算法的适应性:输入的数据的型式,算法效率,算法进度;实际处理问题的需要和目标.总之,针对这一类类别型特征的编码,其目的是将这类结构化的数据映射到一个易于算法处理的空间中.
参考链接
https://zhuanlan.zhihu.com/p/349592092
https://zhuanlan.zhihu.com/p/480609142