文章目录
- 复习——寻找特定中位数
- 新作——最长回文子串
- 个人思路分析
- 实现代码
- 参考学习
- 和上述思路相同,枚举中心点
- 字符串哈希+二分
- 新作——Z 字形变换
- 个人做法
- 思路分析
- 实现代码
- 参考解法
- 分析总结
复习——寻找特定中位数
- 第一次的链接:寻找中位数
- 本来以为已经会做了,第二遍写还是遇到了很多问题,没写出来,有很多参数不是很懂。重新做了一遍,在重新思考,现在懂了。
- k是寻找第几个数字,加上初始坐标应该是 i+k-1
- 当nums1.size() == i,表示对于nums1找个数组而言,已经遍历到头了,所以直接返回nums2即可
- 当k=1,两个数组都没有遍历完,表示在两个有序数组中寻找第一小的数字,不就是比较一下头部吗?
double findMedianSortedArray(vector<int> nums1,vector<int> nums2){
int tot = nums1.size() + nums2.size();
if(tot % 2 == 0){
int left = find(nums1,0,nums2,0,tot / 2 );
int right = find(nums1,0,nums2,0,tot / 2 + 1);
return (left + right) / 2.0;
}else{
return find(nums1,0,nums2,0,tot / 2 + 1);
}
}
int find(vector<int> nums1,int i,vector<int> nums2,int j,int k){
// 保证第一个数组短,第二个数组长
if((nums1.size() - i) > (nums2.size() - j)) return find(nums2,j,nums1,i,k);
// 找第一小的元素,有两个有序列表,就是选择开头元素最小的那个元素即可
// 第一个列表已经遍历完毕了,然后就剩下第二个列表,也是求第一个元素,所以就直接返回
if (k == 1){
if(nums1.size() == i) return nums2[j];
else return min(nums1[i],nums2[j]);
}
// 如果短的数组已经遍历到了最后一个元素,那么剩下的就是在长的数组里面找最终的那个元素,
if (nums1.size() == i) return nums2[j + k - 1];
// 更新转换之后的坐标
int si = min((int)nums1.size(),i + k / 2),sj = j + k - k / 2;
if(nums1[si - 1] > nums2[sj - 1]){
return find(nums1,i,nums2,sj,k - (j - sj));
}else{
return find(nums1,si,nums2,j,k - (i - si));
}
}
新作——最长回文子串
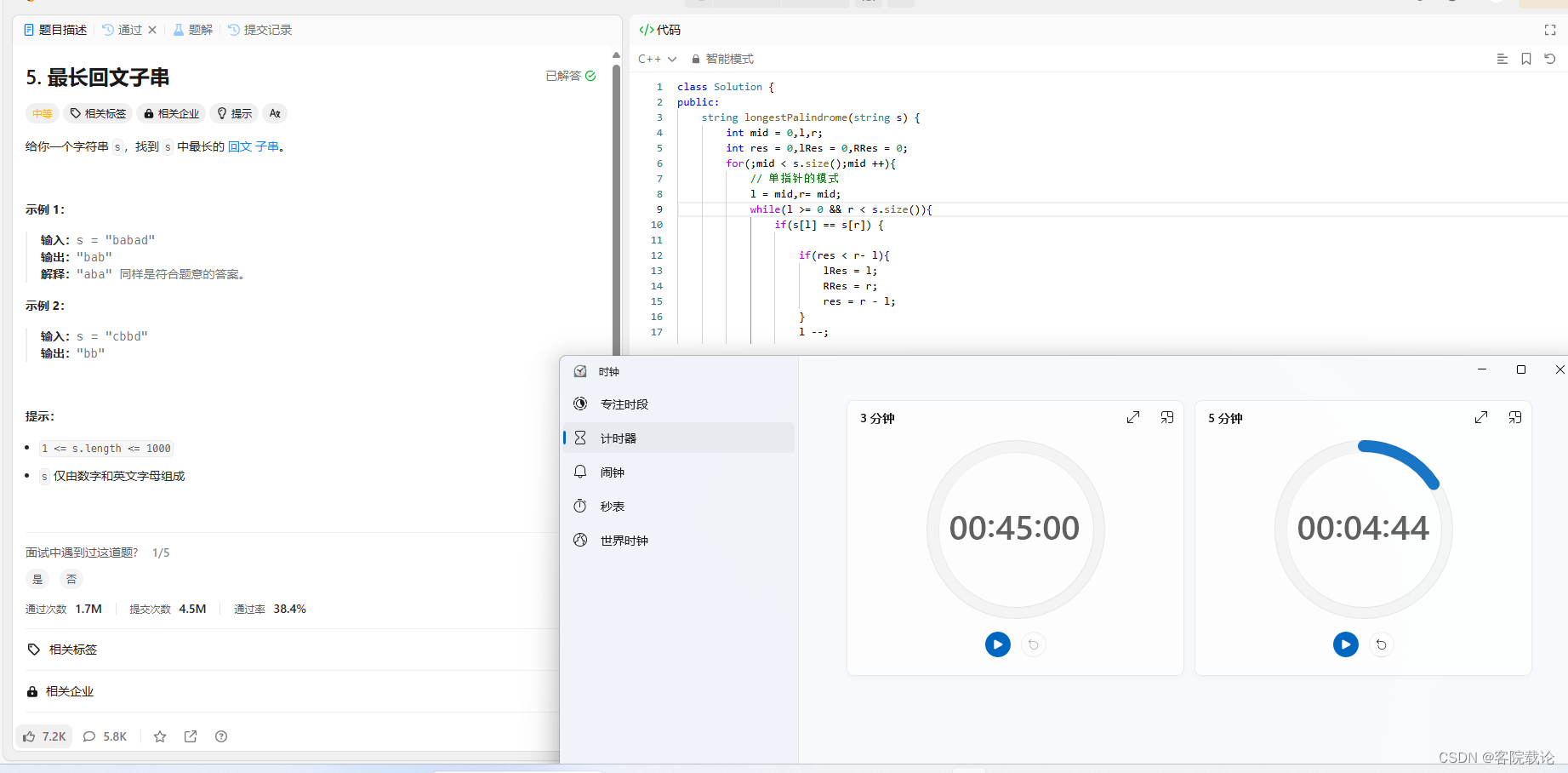
- 嘿嘿,头一次,中等题没做过,二十分分钟写出来,调整出来了。
个人思路分析
- 双指针,但是有两种模式:
- 针对奇数个字符的回文字符串
- 针对偶数个字符的回文字符串
- 还有一个特征
- 长的回文字符串是由短的回文字符串,所以如果不行,就不会存在更长的回文,直接跳转到下一个即可
实现代码
string longestPalindrome(string s) {
int mid = 0,l,r;
int res = 0,lRes = 0,RRes = 0;
for(;mid < s.size();mid ++){
// 奇数的模式
l = mid,r= mid;
while(l >= 0 && r < s.size()){
if(s[l] == s[r]) {
if(res <= r- l){
lRes = l;
RRes = r;
res = r - l;
}
l --;
r ++;
}else
break;
}
// 偶数模式
l = mid,r = mid + 1;
while(l >= 0 && r < s.size()){
if (s[l] == s[r]){
if(res < r- l){
lRes = l;
RRes = r;
res = r - l;
}
l --;
r ++;
}else
break;
}
}
return s.substr(lRes,RRes - lRes);
}
参考学习
和上述思路相同,枚举中心点
- 这里代码写的真简洁,可以好好学习一下
string longestPalindrome(string s) {
string res;
for (int i = 0; i < s.size(); ++i) {
int l = i - 1,r = i + 1;
while(l >= 0 && r < s.size() && s[l] == s[r]) l --,r ++;
if(res.size() < r - l -1) res = s.substr(l + 1,r - l -1);
l = i,r = i + 1;
while(l >= 0 && r < s.size() && s[l] == s[r]) l --,r ++;
if(res.size() < r - l -1) res = s.substr(l + 1,r - l -1);
}
return res;
}
字符串哈希+二分
- 时间不够了,这里贴一下人家的代码和思路吧,还有论文要写,不能花太多时间。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
typedef unsigned long long ULL;
const int N = 2e6 + 10 , base = 131;
ULL hr[N] , hl[N] , p[N];
char str[N];
ULL get(ULL h[] , int l , int r)
{
return h[r] - h[l - 1] * p[r + 1 - l];
}
int main()
{
int T = 1;
while(cin >> str + 1 , strcmp(str + 1 , "END"))
{
int n = strlen(str + 1), res = 0;
for(int i = 2 * n ; i >= 0 ; i -= 2)
{
str[i] = str[i / 2];
str[i - 1] = 'z' + 1;
}
n *= 2; p[0] = 1;
for(int i = 1 , j = n; i <= n ; i ++ , j -- )
{
p[i] = p[i - 1] * base;
hl[i] = hl[i - 1] * base + str[i];
hr[i] = hr[i - 1] * base + str[j];
}
for(int i = 1 ; i <= n ; i ++ )
{
int l = 0 , r = min(n - i , i - 1);
while(l < r)
{
int mid = l + r + 1 >> 1;
if(get(hl, i - mid, i - 1) == get(hr, n + 1 - (i + mid), n + 1 - (i + 1)))l = mid;
else r = mid - 1;
}
if(str[i - l] <= 'z')res = max(res , l + 1);
else res = max(res , l);
}
printf("Case %d: %d\n",T ++ , res);
}
return 0;
}
作者:tom233
链接:https://www.acwing.com/solution/content/33154/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
新作——Z 字形变换

个人做法
思路分析
- 绘制一个二维矩阵,然后找规律,按照规律放到二维矩阵里面,然后在输出对应的矩阵。
- 注意点,以下有一些小细节可以帮助你提高代码的可读性
- 矩阵的坐标从1开始到边界结束,不要从零开始计算
实现代码
string convert(string s, int numRows) {
int row = numRows ,col = s.size() / (numRows * 2 -2) * (numRows - 1);
if (s.size() % (numRows * 2 -2) != 0)
col ++;
char m[row][col];
int sIdx = 0;
string res;
for (int i = 0; i < col; ++i) {
for (int j = 0; j < row; ++j) {
if (sIdx == s.size()) break;
// 竖线模式,顺次往下填
if (i == 0 || i % (numRows - 1) == 0){
m[j][i] = s[sIdx];
res += s[sIdx];
sIdx ++;
}
// 斜线模式,一次往上,主要是判定斜线是都会有对应的元素
else{
int iR = i % (numRows - 1), jR = (row - j - 1 )% (numRows - 1);
if (j != 0 && iR == jR){
m[j][i] = s[sIdx];
res += s[sIdx];
sIdx ++;
}
else
m[j][i] = ' ';
}
}
}
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (m[i][j] != ' ')
res += m[i][j];
}
}
return res;
}
- 这个代码还是有问题,因为是在原来的逻辑上缝缝补补,还有很多漏洞
综合上述观察到的问题,重新进行编程,代码如下
- 虽然很不想承认,但是确实中间那个斜杠的关系表达式,写了半天,没有调整出来,太丢人了,后来补了一个if表达式,始终没有找到能够用一个式子表达的情况!
string convert(string s, int numRows) {
if(numRows == 1 || s.size() == 1) return s;
int row = numRows ,col = s.size() / (numRows * 2 -2) * (numRows - 1);
if (s.size() % (numRows * 2 -2) != 0)
col ++;
char m[row + 1][col + 1];
int sIdx = 0;
string res;
for (int i = 1; i <= col; ++i) {
for (int j = 1; j <= row; ++j) {
if (sIdx == s.size()) break;
// 竖线模式,顺次往下填
if ( i % (numRows - 1) == 1){
m[j][i] = s[sIdx];
sIdx ++;
}
// 斜线模式,一次往上,主要是判定斜线是都会有对应的元素
else{
int iR = i % (numRows - 1) , jR = row - j + 1;
if (iR == 0) iR = (numRows - 1);
if ( iR == jR){
m[j][i] = s[sIdx];
sIdx ++;
}
else
m[j][i] = ' ';
}
}
}
for (int i = 1; i <= row; ++i) {
for (int j = 1; j <= col; ++j) {
if (m[i][j] <= 'Z' && m[i][j] >= 'A')
res += m[i][j];
}
}
return res;
}
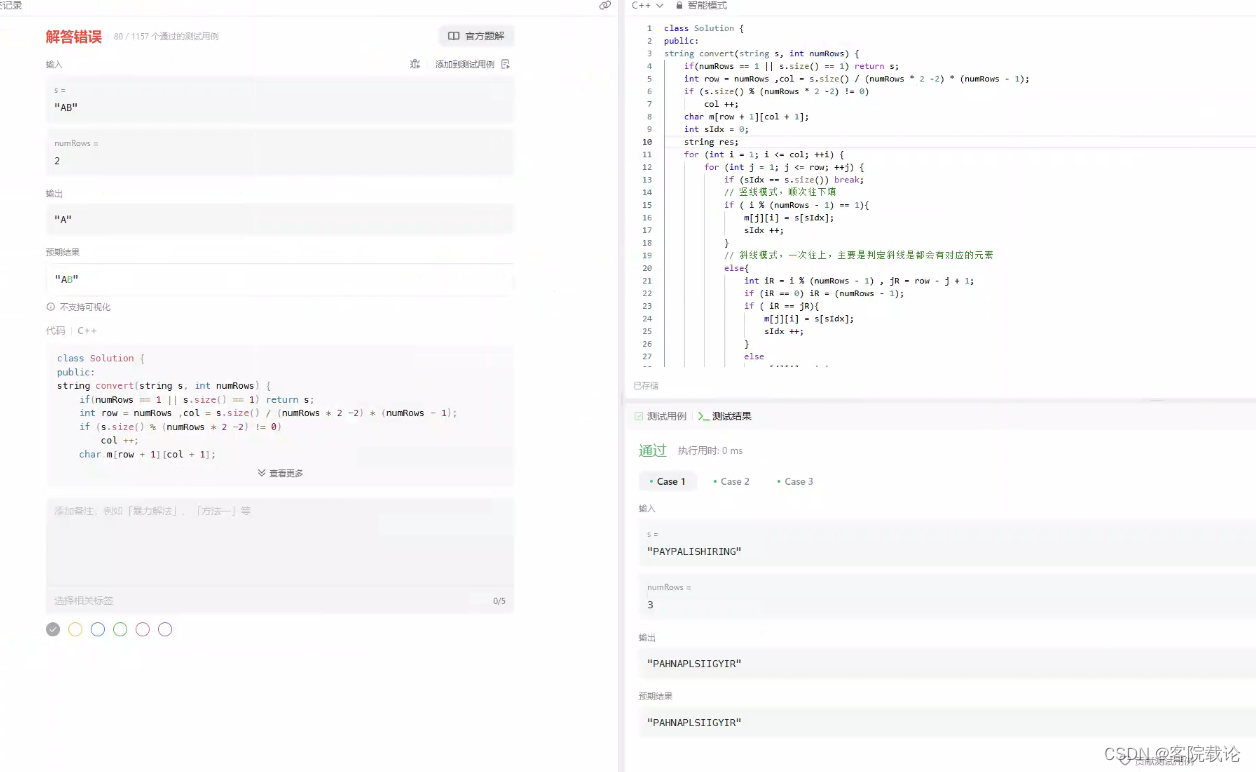
- 还是有部分样例不通过,这里不好费时间了,花了差不多一个半小时,不值得,下次不能再这样了!!
参考解法
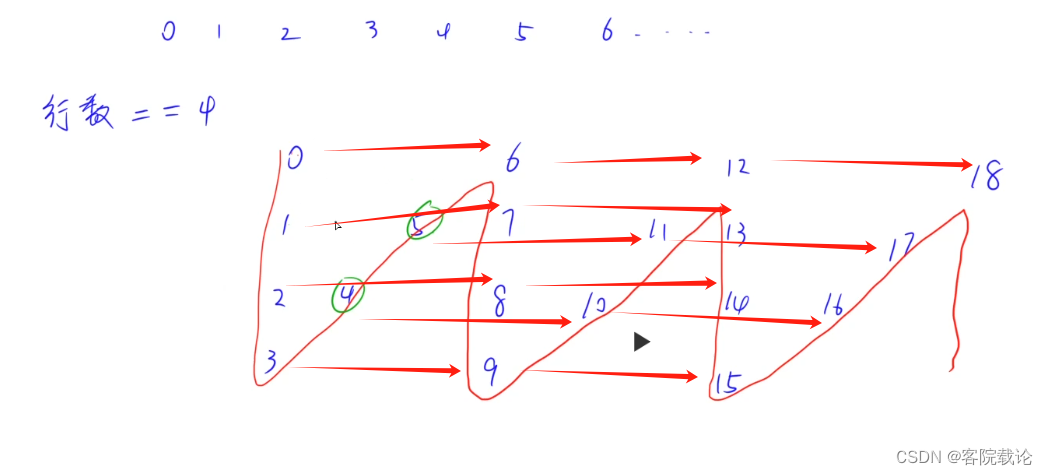
- 直接从根本上找问题,我靠,没有创建数组,然后直接找输出的序列,因为这本来就是一个等差序列,具体如下
- 这个思路真的简洁,我靠,直接从根本上考虑

分析总结
-
矩阵建议不要从零开始,因为要单独处理j为零的情况,出错的概率太高了,不建议,还是从1开始吧
-
要跳出题目去看,不能被限制住。