目录
一、区域Ω的剖分
二、三角形一次元
三、一次元的基函数与面积坐标
四、三角形二次元及其基函数
前两节我们介绍了有限元基本概念和变分理论的推导,本节我们继续探讨有限元空间的构造。
一、区域Ω的剖分
对矩形区域进行三角剖分,其中x方向剖分m份,y方向剖分n份,共得到
个节点及
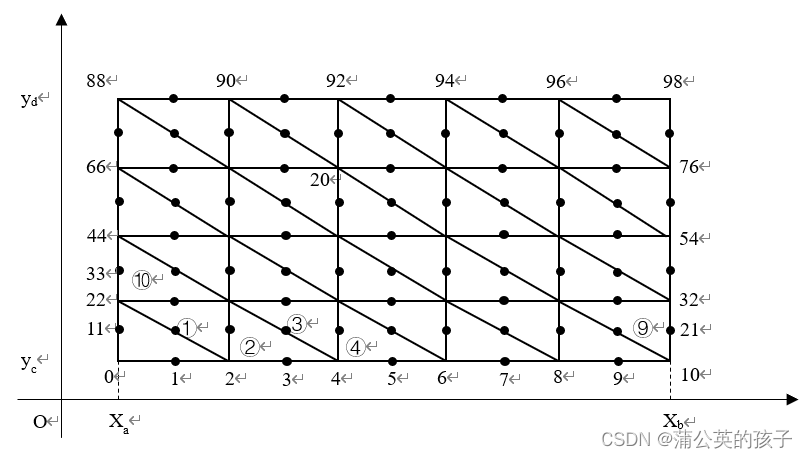
个三角形单元。图1是
的剖分情况,节点编号用数字表示,单元用带圈的数字表示。为了实现后面的程序编写,必须明确单元上的局部编号与整体编号,如图2所示。通过设置剖分数,可以建立单元上整体编号与局部编号之间的关系,可设置二维数组
,第一个参数为单元编号,第二个参数为局部节点编号,如
等,表示第3个单元第0号局部节点的整体节点编号为8,而
则表示第2个单元第1号局部节点的整体节点编号为2。可以通过循环设置所有的节点。


二、三角形一次元
前面两节提到,可以选取为分片连续的一次多项式函数空间,也就是在每个单元e上,
中的函数都是一次多项式,且要保证整体连续。因此对于相邻的两个三角形单元,它们有一条公共边,只要保证分片一次多项式在这条公共边的两个端点(也是剖分节点)处函数值相同即可保证函数整体连续。这样,分片一次多项式在每个单元上的表达式就可以由它在3个顶点处的值唯一确定。下面,在节点
(对应整体编号为i,j,k)的单元e上考虑数值解
的表达式,尝试用基函数来表示
,其中
为待定基函数,满足以下性质:
且它们都是一次函数。这样,数值解在单元e上的表达式完全由它在3个顶点处
处的值
决定,
可以看作精确解u在整体编号i,j,k的节点处的近似。一旦把所有
求出来(边界点除外,因为
从而边界节点处
的值为零),则数值解
的表达式也就确定了。所以现在的基本问题是对离散问题式
求,使得
建立的关系式。
三、一次元的基函数与面积坐标
由于基函数在单元e上是一次多项式,尝试设,其中a,b,c为待定系数,且单元e上s号节点
的坐标为
,则由条件公式(1)可知:
从而解出
代入可得
可以证明以(逆时针排列)为顶点的三角形单元e的面积
。
于是,若内有一点P的坐标为
,如图3所示,则
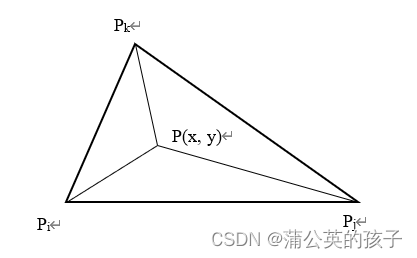
同理,
注意到,显然有
也就是说不是相互独立的。换言之,
内任一点
,必然可以唯一对应一组坐标
,基函数
被称为重心坐标。由于它们又都是三角形的面积比,所以它们也称为面积坐标。面积坐标在有限元分析中非常重要,它是从一般单元变化到标准单元的工具,也是进行Sobolev空间范数估计的有效手段。事实上,公式(4)、(5)可以反解出直角坐标
与重心坐标之间的对应关系式:
从而可以实现将一般的三角形单元变换成标准单元
,如图4所示。

四、三角形二次元及其基函数
我们除了可以选取为分片连续的一次多项式函数空间外,也可以选取
为分片连续的二次多项式函数空间,也就是在每个单元e上,
中的函数都是二次多项式,且要保证整体连续。因此在每个单元e上,
中的分片二次多项式函数
就形如
,其中
均为待定常数,从而需要有6个条件来唯一确定这个表达式。与一次元相似,要确定这6个常数,我们可以取三角形单元e的3个顶点及3条边的中点值作为条件(这些条件称为自由度),即分片二次多项式在每个单元上的表达式就可以由它在这个单元3个顶点和3条边的中点处的值唯一确定,这样也可以保证函数的整体连续性。事实上,在相邻的两个三角形单元上的公共边上,位置变量x和y有一个直线方程的线性约束,从而
在这条边上成为一个只关于自变量x的二次函数,这个函数在3个不同的点(两个顶点和一个中点)上取值相同,说明
在公共边上的表达式所示唯一确定的,也就是说,这个分片二次多项式在相邻两个单元上虽然整体表达式不相同,但在其公共边上表达式相同,这就保证了函数在
上整体连续,从而实现
。
对于以上的三角形二次元,由于涉及到三角形单元的中点,所以尽管三角形剖分情况不变,即共有2mn个三角形单元,但整体节点数变为个,且节点的编号将随之发生改变。例如,图1将变为图5。
接下来,在单元e上考虑数值解的表达式,其中e的3个顶点为
(对应整体编号为i,j,k),3条边的中点为
(对应整体编号为
),如图6。
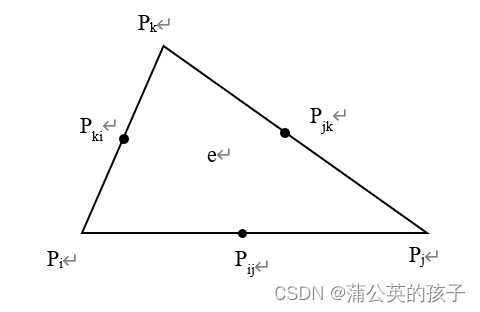
在单元e上的表达式尝试用基函数表示为
其中为待定基函数,满足以下性质:
利用重心坐标,很容易将上述基函数表示出来,即有分别对应于三角形单元3个顶点的基函数:
及对应于三角形3条边中点的 基函数:
至此,数值解 在单元e上的表达式就确定为:
综上,有限元空间由一个三元组
确定。具体的,设
是区域Ω的一个剖分,e是剖分
中的单元,参数h定义为所有单元的最大直径,即
,
是选定的分片多项式函数空间,
是每个e上用于唯一确定
内的多项式函数所需要的条件。