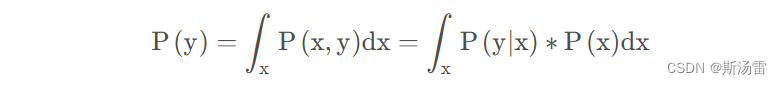之前读完了3D高斯泼溅，收获颇丰，可没想到的是2D高斯泼溅也在三月份接踵而至。让我们一起解读一下！
论文地址: 2D Gaussian Splatting for Geometrically Accurate Radiance Fields
代码地址: 2d-gaussian-splatting

一. 论文解读

Abstract

作者认为，3D高斯虽然最近很火，但是它也有一个比较大的缺陷——**由于多视图的不一致性，3D高斯泼溅无法很好的表示物体的几何表面。**因此作者提出了2D高斯泼溅，其核心在于 将3D体积折叠为一组2D定向平面高斯圆盘。 2D高斯泼溅能够在建模表面时提供视图一致的几何表面。为了精准恢复薄表面和稳定优化，作者引入了 基于光线投射和光栅化的视角精确2D泼溅过程，并且加入了深度失真和法向一致性来确保重建的质量。

1.1 Introduction

作者首先提出来过去的工作不咋样balabala，然后转而引入自己的2D高斯泼溅。
2D高斯泼溅使用基元来表示物体，每个基元定义为一个定向的椭圆形圆盘。
具体来说，3DGS在像素射线和3D高斯的交点处评估高斯值，这导致从不同视点渲染时深度不一致。相反，2DGS的方法利用显式的射线-泼溅交点，导致视角准确的泼溅，此外，2D高斯基元中的固有表面法线通过法线约束实现了直接的表面正则化。

然而只依靠光度损失来重建仍然存在问题，为了增强重建并实现更光滑的表面，作者引入了两个正则化项：**深度失真和法线一致性。**深度失真项集中处理沿射线分布在狭窄范围内的2D基元，解决了渲染过程中忽略高斯之间距离的限制。法线一致性项最小化渲染法线图与渲染深度梯度之间的差异，确保由深度和法线定义的几何体对齐。

总而言之，本篇论文的contribution如下：

• 作者提出了一种高效的可微分2D高斯渲染器，通过利用2D表面建模、射线-泼溅交点和体积积分，实现了视角准确的泼溅。
• 作者引入了两个正则化损失，用于改进和无噪声的表面重建。
• 我们的方法相比其他显式表示方法，在几何重建和新视图合成结果上达到了最新的水平。

如下图所示就是3DGS和2DGS在几何表面的差异。左边是3DGS,右边是2DGS，可以看出，当相机在左边和右边分别观察时，3DGS的两次观察结果的交点平面是不一致的。而2DGS可以确保看到的是同一个平面。

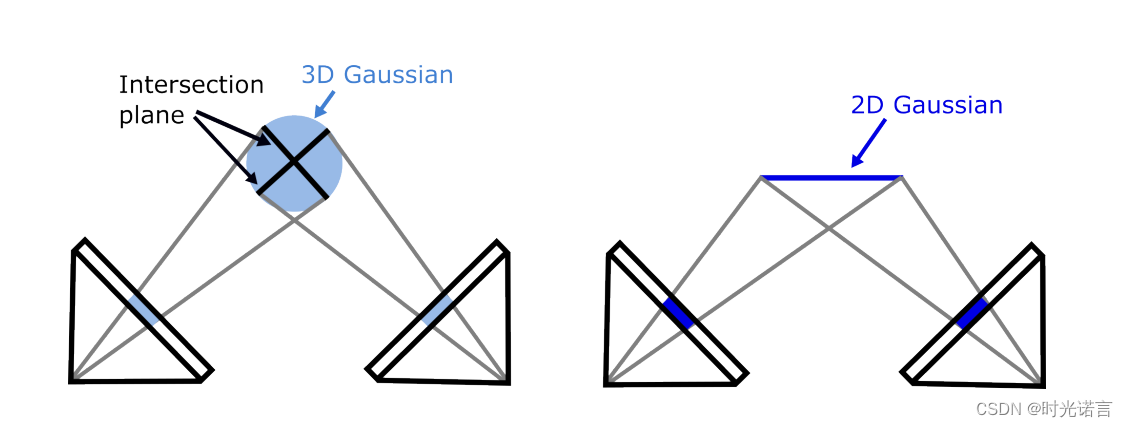
1.2 Related Work

1.2.1 新视角合成

作者在这一段中再次总结了NeRF与3DGS的工作，然后再次强调2DGS怎么怎么好。
我这里有一篇快速了解NeRF和3DGS的文章：
NeRF与3DGS速通

1.2.2 3D重建

这部分同样没什么好说的，作者提出2DGS将重建速度提高了一个数量级。但是我认为这很有可能在3DGS中就已经达成。

1.2.3 可微分的基于点的图形

作者提出，本文他们将展示使用2D高斯基元进行详细的表面重建。还强调了在优化过程中额外正则化损失的重要作用，展示了它们对重建质量的显著影响。

然后作者礼貌起见，还是把3DGS单列出来提了一嘴hh

1.2.4 最近的工作

**最近的工作就是3DGS,SuGaR以及NeuSG。**与SuGaR不同，SuGaR使用3D高斯近似2D高斯，而我们的方法直接采用2D高斯，简化了过程并增强了结果几何，而无需额外的精细化。NeuSG联合优化3D高斯基元和隐式SDF网络，并仅从SDF网络中提取表面，而我们的方法利用2D高斯基元进行表面近似，提供了一种更快且概念上更简单的解决方案。

1.3 3DGS

在3DGS这篇文章中，相关的作者使用3D基于的形式来表示物体：
$$\mathcal{G}(\mathbf{p})=\exp \left(-\frac{1}{2}{\left(\mathbf{p}-{\mathbf{p}}_k\right)}^{\top }{\Sigma }^{-1}\left(\mathbf{p}-{\mathbf{p}}_k\right)\right)$$
其中3D维度下，坐标之间的协方差矩阵近似计算公式为：
$$\Sigma ={\mathbf{RSS}}^{\top }{\mathbf{R}}^{\top }$$
之后，为了最终实现在2D层面的渲染，3D视角通过视图变化矩阵W（先转化为相机视角），再乘以投影矩阵J得到了2D层面的协方差矩阵。
$${\Sigma }^{\prime }=\mathbf{JW}\Sigma {\mathbf{W}}^{\top }{\mathbf{J}}^{\top }$$
最后，实现像素级别的重建：
$$\mathbf{c}(\mathbf{x})=\sum _{k=1}^K{\mathbf{c}}_k{\alpha }_k{\mathcal{G}}_k^{2D}(\mathbf{x})\prod _{j=1}^{k-1}\left(1-{\alpha }_j{\mathcal{G}}_j^{2D}(\mathbf{x})\right)$$

然而（作者是会写论文的，每隔几段就要批评一下3DGS来凸显自己hh），3DGS在表面重建中遇到了很大的挑战：
首先，3D 高斯的体积辐射表示与表面的薄性质相冲突。其次，3DGS 无法本质上建模表面法线，但是这一点对于高质量表面重建至关重要。第三，3DGS 的光栅化过程缺乏多视图一致性，导致不同视点的 2D 交点平面不同 。此外，使用仿射矩阵将 3D 高斯转换到射线空间仅在中心附近产生准确的投影，在周围区域则牺牲了视角准确性 。

其实总而言之，作者硬是把一个创新拉成三个。作者最大的贡献点就是解决了几何表面的重建不准确问题，记住这一点就好。

1.4 2DGS正式出场

1.4.1 模型架构

作者通过采用嵌入在3D空间中的“平坦”2D高斯来简化三维建模。在二维高斯模型中，2D基元将密度分布在平面圆盘内，并将法线定义为密度变化最剧烈的方向。
接下来是2DGS的数学解释，前方高能！！！

首先我们可以找一个三维空间的点Pk作为一个基元建模的中心点，这个Pk同样是二维高斯分布的中心点。此外我们还知道两条主切向量tu和tv。根据tu和tv便可计算出发现向量及方向：${\mathbf{t}}_w={\mathbf{t}}_u\times {\mathbf{t}}_v$,由此得到的旋转矩阵$\mathbf{R}=\left[{\mathbf{t}}_u,{\mathbf{t}}_v,{\mathbf{t}}_w\right]$是一个3×3的矩阵。除此之外，会有一个3×3的缩放对角矩阵，且该对角矩阵的最后一项（右下角那一项）为0。

这样，其实我们得到了2D坐标系下的一系列向量，那么可以经过一系列变化得到一个三维空间的点$\mathbf{P}(\mathbf{u},\mathbf{v})$。完整公式如下：
$$\begin{array}{rl}P(u,v)& ={\mathbf{p}}_k+s_u{\mathbf{t}}_{u}u+s_v{\mathbf{t}}_{v}v=\mathbf{H}(u,v,1,1{)}^{\top }\\ \text{ where }\mathbf{H}& =\left[\begin{array}{cccc}{s}_u{\mathbf{t}}_u& s_v{\mathbf{t}}_v& 0& {\mathbf{p}}_k\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cc}\mathbf{RS}& {\mathbf{p}}_k\\ 0& 1\end{array}\right]\end{array}$$

我们举个例子：假设有如下参数，
$\begin{array}{l}{\mathbf{p}}_{\mathbf{k}}=[1,1,1]\\ {\mathbf{t}}_{\mathbf{u}}=[1,0,0]\\ {\mathbf{t}}_{\mathbf{v}}=[0,1,0]\\ s_u=2\\ s_v=3\\ u=0.5\\ v=0.5\end{array}$
通过公式计算可以得到：
$P(u,v)=[1,1,1]+2\cdot [1,0,0]\cdot 0.5+3\cdot [0,1,0]\cdot 0.5=[1,1,1]+[1,0,0]+[0,1.5,0]=[2,2.5,1]$

P(u,v)表示在三维空间中的具体点，是通过局部切平面的二维坐标 (u,v) 转换得到的。这个转换考虑了中心点、主切向量和缩放因子的影响，使得二维高斯分布可以嵌入到三维空间中。最后的(u,v,1,1)则是在齐次四维空间表示的坐标。

需要补充的是，对于uv空间的点(u,v),它的2D高斯可以通过2D标准高斯公式评估：
$$G(\mathbf{u})=\exp \left(-\frac{u^2+v^2}{2}\right)$$

1.4.2 泼溅

作者通过找到三个位于不同平面上的交点来高效地定位射线-泼溅交点。
给定图像坐标 x=(x,y)，我们将像素的射线参数化为两个正交平面（x平面和y平面）的交点。具体来说，x平面由法向量(−1,0,0) 和偏移量 x 定义。因此，x平面可以表示为一个四维齐次平面hx=(−1,0,0,x)。类似地，y平面为hy=(0,−1,0,y)。因此，射线r=(x,y) 由x平面和y平面的交点决定。

接下来，我们将这两个平面变换到二维高斯基元的局部坐标系，即uv坐标系，注意，使用变换矩阵 M 在平面上变换点等效于使用逆转置${\mathbf{M}}^{-T}$变换齐次平面参数。因此，应用$(\mathbf{WH}{)}^{-1}$等效于使用$(\mathbf{WH}{)}^T$,消除了显式矩阵逆运算，并得出：
$${\mathbf{h}}_{\mathbf{u}}=(\mathbf{WH}{)}^T{\mathbf{h}}_{\mathbf{x}}{\mathbf{h}}_{\mathbf{v}}=(\mathbf{WH}{)}^T{\mathbf{h}}_{\mathbf{y}}$$
之前我们得知，二维高斯平面上的点可以表示为$(u,v,1,1)$,同时，交点应位于变换后的x平面和y平面上，因此：
$${\mathbf{h}}_{\mathbf{u}}\cdot (u,v,1,1{)}^T={\mathbf{h}}_{\mathbf{v}}\cdot (u,v,1,1{)}^T=0$$
这导致了交点u(x) 的有效解：
$$u(\mathbf{x})=\frac{{\mathbf{h}}_u^2{\mathbf{h}}_v^4-{\mathbf{h}}_u^4{\mathbf{h}}_v^2}{{\mathbf{h}}_u^1{\mathbf{h}}_v^2-{\mathbf{h}}_u^2{\mathbf{h}}_v^1}v(\mathbf{x})=\frac{{\mathbf{h}}_u^4{\mathbf{h}}_v^1-{\mathbf{h}}_u^1{\mathbf{h}}_v^4}{{\mathbf{h}}_u^1{\mathbf{h}}_v^2-{\mathbf{h}}_u^2{\mathbf{h}}_v^1}$$
其中，$h_i^l$和$h_j^l$是四维齐次平面参数的i-th参数。

除此之外，作者考虑到了其他的特殊解情况：

退化解 (Degenerate Solutions)： 当二维高斯从倾斜角度观察时，在屏幕空间中可能会退化为一条线。这意味着在光栅化过程中，高斯分布可能会被忽略，从而导致渲染结果的精度降低。
为了处理这种情况，论文引入了一个低通滤波器来稳定优化过程。具体方法如下：
最大值滤波器：定义了一个新的高斯值$\hat{\mathcal{G}}(x)$,它取原始高斯值$\mathcal{G}(\mathbf{u}(x))$和低通滤波器值$\mathcal{G}\left(\frac{\mathbf{x}-\mathbf{c}}{\sigma }\right)$的最大值。这样可以确保即使在退化情况下，二维高斯分布仍然能被正确处理。
其中,$u(\mathbf{x})$由上面的方程解给出，c是中心pk的投影。直观地说，$\hat{\mathcal{G}}(x)$ 由固定的屏幕空间高斯低通滤波器限定，该滤波器的中心为 ck且半径为σ，在实验中，作者设置$\sigma =\sqrt{2}/2$以确保在渲染过程中使用足够的像素。

光栅化 (Rasterization):
光栅化是将高斯分布从几何表示转换为屏幕上的像素表示的过程。具体步骤如下：

1. 计算屏幕空间边界框：为每个高斯基元计算屏幕空间的边界框，用于确定哪些像素会被影响。
2. 深度排序和瓦片组织：根据高斯分布中心的深度进行排序，并根据边界框将它们组织成瓦片。这有助于优化渲染过程。
3. 体积 alpha 混合：使用体积 alpha 混合从前到后集成高斯分布的 alpha 加权外观。这种方法确保了最终渲染图像的透明度和深度信息的正确处理。
   alpha 混合过程如下：
   $$\mathbf{c}(\mathbf{x})=\sum _{i=1}{\mathbf{c}}_i{\alpha }_i{\hat{\mathcal{G}}}_i(\mathbf{u}(\mathbf{x}))\prod _{j=1}^{i-1}\left(1-{\alpha }_j{\hat{\mathcal{G}}}_j(\mathbf{u}(\mathbf{x}))\right)$$
   参数解释如下：
   

1.5 Training

作者们的二维高斯方法虽然在几何建模上有效，但在仅使用光度损失进行优化时可能会导致重建结果的噪声问题，这是三维重建任务固有的挑战。因此，作者提出来深度失真和法线一致性两个关键术语。

1.5.1 深度失真

问题：当使用三维高斯分布进行渲染时，不同高斯分布可能会在深度上有交叠，这会导致渲染结果中的深度和颜色出现混乱，特别是在不同的高斯分布看起来很接近但实际上应该有不同深度时。

解决方案：因此，引入深度失真正则化项，通过最小化交点之间的深度差距，来确保这些高斯分布在正确的深度位置上。这可以帮助集中权重分布，使得重建的几何形状更加清晰和准确。
公式如下：
$${\mathcal{L}}_d=\sum _{i,j}{\omega }_i{\omega }_j\left|z_i-z_j\right|$$

1.5.2 法线一致性

问题：在渲染过程中，如果二维高斯分布的法线（指向相机的方向）不一致，会导致表面不光滑，看起来不自然。特别是在处理半透明表面时，这个问题会更明显。
解决方案：引入法线一致性正则化项，通过对齐二维高斯分布的法线和实际表面的法线，确保重建的表面是光滑的，且局部几何形状准确。这意味着二维高斯分布的法线要与由深度图估计的表面法线一致。

作者将二维高斯分布泼溅的法线与深度图的梯度对齐，公式如下：
$${\mathcal{L}}_n=\sum _i{\omega }_i\left(1-{\mathbf{n}}_i^{\top }\mathbf{N}\right)$$
其中,i表示射线上的交叉泼测索引，$\omega$ 表示交点的混合权重，${\mathbf{n}}_i$代表泼测朝向相机的法线， $\mathbf{N}$是由附近深度点p估计的法线。具体来说，$\mathbf{N}$通过有限差分计算如下:
$$\mathbf{N}(x,y)=\frac{{\nabla }_x\mathbf{p}\times {\nabla }_y\mathbf{p}}{\left|{\nabla }_x\mathbf{p}\times {\nabla }_y\mathbf{p}\right|}$$
通过将泼溅法线与估计的表面法线对齐，作者确保二维泼溅在局部上逼近实际物体表面。

1.5.3 实验中用到的损失函数

本实验最终的损失函数公式如下：
$$\mathcal{L}={\mathcal{L}}_c+\alpha {\mathcal{L}}_d+\beta {\mathcal{L}}_n$$
参数解释如下：

作者通过实验得出，设定 α=1000 用于有界场景，α=100 用于无界场景，β=0.05 适用于所有场景。

时间原因，代码解析以后有空再更吧。