1.定义
图的每个结构之间有着某种关系。
六度空间理论等;
1.1引子:
最短路径问题
1.2什么是图
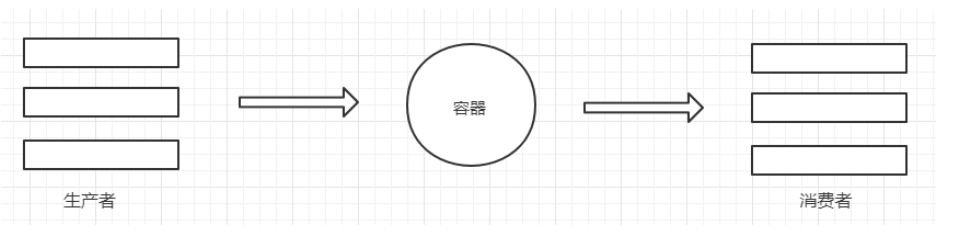
- 表示一种多对多的关系
线性关系表示的是一对一的关系,树表示的是一对多的关系。其实线性表和树其实都可以认为是图的一种特殊的情况。 - 包含:
1)一组顶点:通常使用V(Vertex)表示顶点集合
2)一组边:通常使用E(Edge)来表示边的集合,表示的是顶点和顶点之间的某种关系:
图是双向或者单向的,不考虑重边和自回路

1.3抽象数据类型定义

非空:一个图可以一条边都没有,但是必须要有顶点V
1.4常见术语
1)无向图:图中所有的边都是无所谓方向的
2)有向图:图中的边是有方向的,可能单向,可能双向,总之方向对它很重要
3)网络:在图的每条边上加上数字(权重),权重可以有多种现实意义。比如路的长度;事件频率;
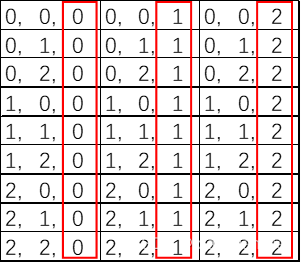
2.邻接矩阵表示法
2.1
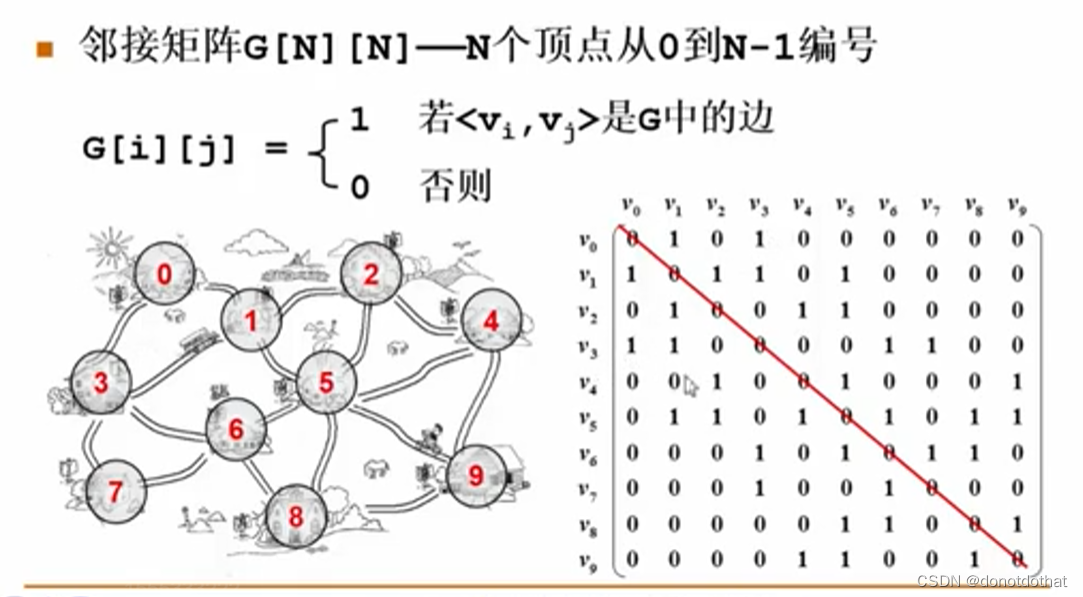
其中,每个顶点使用Vi 来表示,如果顶点之间有关系,也就是有边连接,[Vi][Vk]的值就为1。两个顶点之间没有关系,值为0。
特点:
- 矩阵对角线(v0,v0) ,(v1,v1)…都是0。因为不允许自回路;
- 无向图的邻接矩阵是对称的,存了两遍。
2.2怎样省一半空间
因为是对称的,所以一半的空间是浪费的。
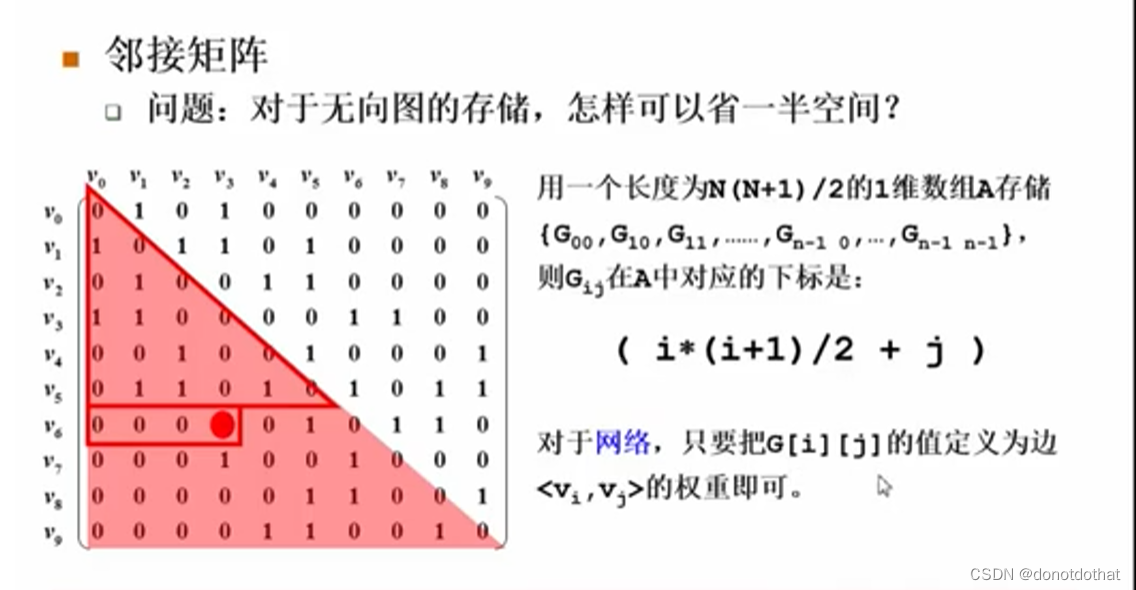
例如只储存下三角区域的元素,将各个顶点按照自上而下的顺序储存在一个线性表中。
- 线性表的大小:
使用等差求和的方式,自上而下相加计算; - G(i,j)在数组中对应的下标:
由于从上到下是按顺序排开的,所以照样可以使用等差数列求和的方式。第i行之前有i行,先计算满的i行;在第i行,V(i,j)之前有j个元素。那么在整个数组中,在他之前一共有( i*(i+1)/2 + j )个元素。又因为下标从0开始,则他的下标就是( i*(i+1)/2 + j );
2.3邻接矩阵的优点

1.找一个顶点的所有邻接点:
邻接点的定义:有直接的边和该顶点相接的顶点
1)无向图:直接扫描该顶点所在的那一行,值为1就是它的邻接点,因为无向图的邻接矩阵是对称的;
2)有向图:不仅要扫描该顶点所在的那一行,还要扫描他所在的那一列,因为不对称;
2.度的概念
1)对于无向图,度就是一个顶点向周围有的边数;
2)对于有向图,从该顶点出发的边数为出度,指向该点的边数为入度
计算任一顶点的度:
1)无向图:扫描对应的行/列 非0元素的个数
2)有向图:
<1>出度的个数:扫描对应行第i行非0元素的个数。对应行非0元素的个数就是从该顶点指向其他顶点的边数;
<2>入度的个数:扫描对应列第i列非0元素的个数。对应列非0元素的个数就是指向它的边的个数。
2.4邻接矩阵的缺点
1)浪费空间:
当一个图中的顶点很多,但是边很少时(稀疏图)就会有大量的0,大量无效元素;对于稠密图(特别是完整图,边的数量达到最大 )还是很高效的
2)浪费时间:
对于稀疏图,要统计图中一共有多少条边,由于1的个数很少,所以遍历的时候很浪费时间。

3.邻接表表示法
3.1
为了解决稀疏图的储存问题,邻接表是存储链表的数组(嵌套),G[N]为指针数组。对应每一个顶点,定义一个指针,这个指针后面链接着非0元素(边),存成一个链表;邻接矩阵的元素0不会储存到链表中。
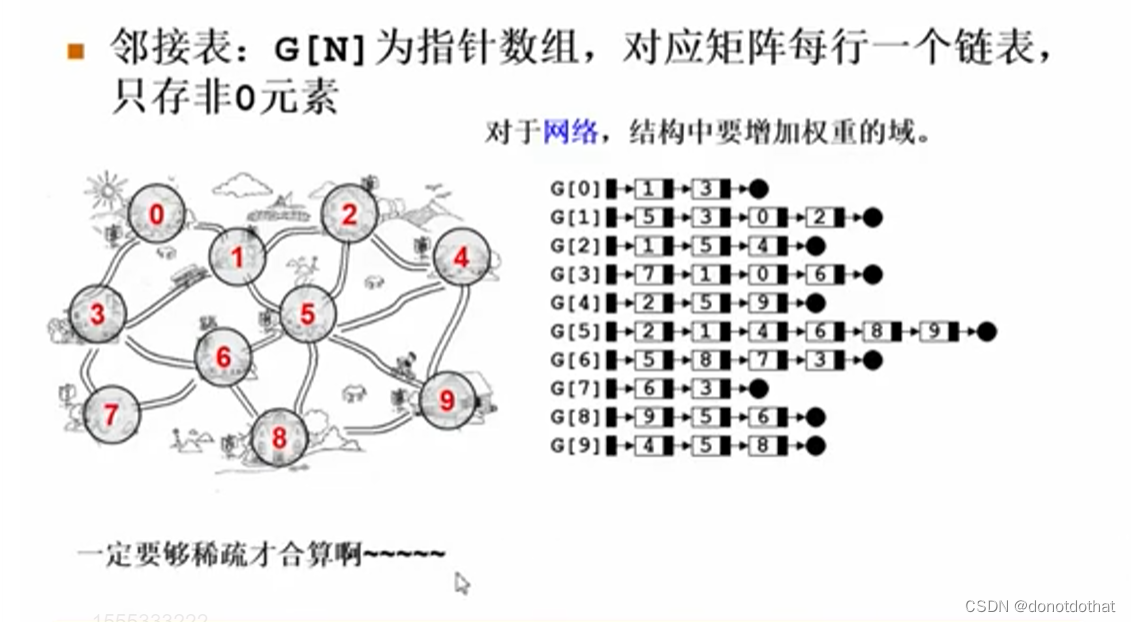
1)首先要对每一个顶点开一个指针,如果有10个顶点,数组中就会有10条链表;数组的元素是一个头指针。
2)注意邻接表的表示法是不唯一的,因为在每一串链表中,顶点的顺序是无所谓的。
3)空间占用对比
<1>在邻接矩阵中,每一条边占据一个整数的位置,如果有权重,可以将1改为权重的大小,0还是代表没有边存在;
<2>在无向图的邻接表中,每个边的关系还是被储存了两遍,顶点序号占据一个数据域,指向下一个顶点占据一个指针域。对于网络来说,还有权重,还需要再开一个数据域。
所以,只有图足够稀疏,使用邻接表才是合算的。
3.2 邻接表的特点
1)方便寻找任一顶点的所有邻接点。只要顺着顶点所在的链表找下去就好;
2)节约稀疏图的空间
邻接表所占的空间:需要V个头指针 + 2*E个结点(因为每个边的关系要存储两遍),如果不考虑权重,其中每个节点要至少2个域。
3)计算任一顶点的度
<1>无向图:只需要计算出对应链表有多少结点
<2>有向表:只能计算出度,即有向表的邻接表表示储存的是由该顶点指向外的边;如果要计算入度,需要构造“逆邻接表”储存指向自己的边来方便计算,那么一个顶点结构就包括两个链表;
4)邻接表不方便检查任意一对顶点间是否存在边
4.图的建立(代码篇)
4.1邻接矩阵
1.定义:
#define MaxVertexNum 100 /* 最大顶点数设为100 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
struct GNode//打包一个图的结构
{
int Nv;//顶点数
int Ne;//边数
WeightType G[MaxVertexNum][MaxVertexNum];
//WeightType的类型看权重是什么数据类型,这里面储存0和非0
//DataType Data[Num];这个数组可以储存顶点带有的数据
};
typedef struct GNode* PtrToGNode;
typedef PtrToGNode MGraph;
2.初始化:
先建立图的顶点,给定要建立的图的顶点个数,先创建一个没有边的图
MGraph CreatGraph( int VertexNum )
{
MGraph Graph = malloc(sizeof(struct GNode));//一旦分配号好内存,矩阵就已经建立好了
Graph->Nv = VertexNum;//顶点的个数
Graph->Ne = 0;
for(Vertex V = 0 ;V<Graph->Nv;V++)
for(Vertex W = 0;W<Graph->Nv;W++)
Graph->G[V][W] = 0;//全为0,表示没有边
return Graph;
}
这样就初始化完成了有所有的顶点但是没有边的图
3.在图中插入边:
//先定义边结构 每条边就是一个结构体
struct ENode
{
Vertex V1,V2;//决定有向边的两个顶点<V1,V2>
WeightType Weight;//如果有权重
};
typedef struct ENode* PtrToENode;
typedef PtrToENode Edge;//可读性
void InsertEdge( MGraph Graph, Edge E )
{
//有向图,插入V1->V2即可
Graph->G[E->V1][E->V2] = E->Weight;//如果没有权重,就赋值为1
//无向图,双向,还要插入V2->V1:
//Graph->G[E->V2][E->V1] = E->Weight;
}
4.建立完整图
输入格式:
Nv Ne
V1 V2 Weight
V1 V4 Weight
··· ···
MGraph BuildGraph()
{
//首先读入顶点数
int Nv;
scanf("%d",&Nv);
//基于定点数就可以建立图
MGraph Graph = CreateGraph(Nv);
//读入图的边数
scanf("%d",&(Graph->Ne);
if(Graph->Ne != 0 )//边数不为空才可
{
//创建一个临时储存边的结构
Edge E = malloc(sizeof(struct ENode));
for(int i = 0;i<Graph->Ne;i++)
{
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);//有多少条边,就读入多少次
InsertEdge(Graph,E);//每读一次,紧跟着插入边
}
}
//如果有顶点数据的话
for(Vertex V = 0;V<Nv;V++)
{
scanf("%c",&Graph->Data[V]);
}
return Graph;
}
如果是在考试,不写函数,快速建立一个图:

直接将邻接矩阵和点数、边数设置成全局变量,所以无需指针,无需传入参数,在函数内部直接访问即可;
读入顶点数,先来一个二重循环,将矩阵中所有的元素初始化为0;读入边数,然后读入边对应的点,传入权重或者1。
4.2邻接表
所谓邻接表,就是指针数组,矩阵每一行对应一串链表。有多少行就是有多少条链表,只存非0元素。
#include <stdio.h>
#include <stdlib.h>
// 图的最大顶点数
#define MAX_VERTICES 100
// 图的邻接表中的节点
struct AdjListNode {
int dest; // 该顶点的编号
struct AdjListNode* next; // 指向下一个邻接节点的指针
};
// 图的邻接表
struct AdjList {
struct AdjListNode* head; // 指向邻接表头节点的指针
};
// 图本身结构
struct Graph {
int V; // 图中顶点的数量
struct AdjList* array; // 邻接表数组 (结构体数组)
};
// 创建新的邻接表节点
struct AdjListNode* newAdjListNode(int dest) {
struct AdjListNode* newNode = (struct AdjListNode*)malloc(sizeof(struct AdjListNode));
newNode->dest = dest; // 设置顶点编号
newNode->next = NULL; // 初始化下一个节点指针为NULL
return newNode; // 返回新创建的邻接表节点
}
// 创建图
struct Graph* createGraph(int V) {
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V; // 设置图的顶点数量
// 创建V个邻接表
graph->array = (struct AdjList*)malloc(V * sizeof(struct AdjList));
// 初始化每个邻接表的头节点为NULL
for (int i = 0; i < V; ++i) {
graph->array[i].head = NULL;
}
return graph; // 返回新创建的图
}
// 添加边到图
void addEdge(struct Graph* graph, int src, int dest) {
// 添加从src到dest的边
struct AdjListNode* newNode = newAdjListNode(dest);
newNode->next = graph->array[src].head; // 将新节点的下一个指针指向当前的头节点
graph->array[src].head = newNode; // 将头节点更新为新节点
// 如果是无向图,添加从dest到src的边
newNode = newAdjListNode(src);
newNode->next = graph->array[dest].head; // 将新节点的下一个指针指向当前的头节点
graph->array[dest].head = newNode; // 将头节点更新为新节点
}
// 打印图的邻接表表示
void printGraph(struct Graph* graph) {
for (int v = 0; v < graph->V; ++v) {
struct AdjListNode* pCrawl = graph->array[v].head; // 获取顶点v的邻接表头节点
printf("\n Adjacency list of vertex %d\n head ", v);
while (pCrawl) { // 遍历邻接表
printf("-> %d", pCrawl->dest); // 打印目标顶点
pCrawl = pCrawl->next; // 移动到下一个邻接节点
}
printf("\n");
}
}
int main() {
// 创建一个有5个顶点的图
int V = 5;
struct Graph* graph = createGraph(V);
// 添加边
addEdge(graph, 0, 1);
addEdge(graph, 0, 4);
addEdge(graph, 1, 2);
addEdge(graph, 1, 3);
addEdge(graph, 1, 4);
addEdge(graph, 2, 3);
addEdge(graph, 3, 4);
// 打印图的邻接表表示
printGraph(graph);
return 0;
}
其中比较难以理解的点:
-
整个程序有三个结构体,从大到小依次是图结构【包括顶点数和邻接表(数组)】、邻接表结构(是数组,每个数组元素是一个结构体结点)、 邻接表的节点结构(包括关系顶点和指向下一节点的指针域)
-
整个图结构:
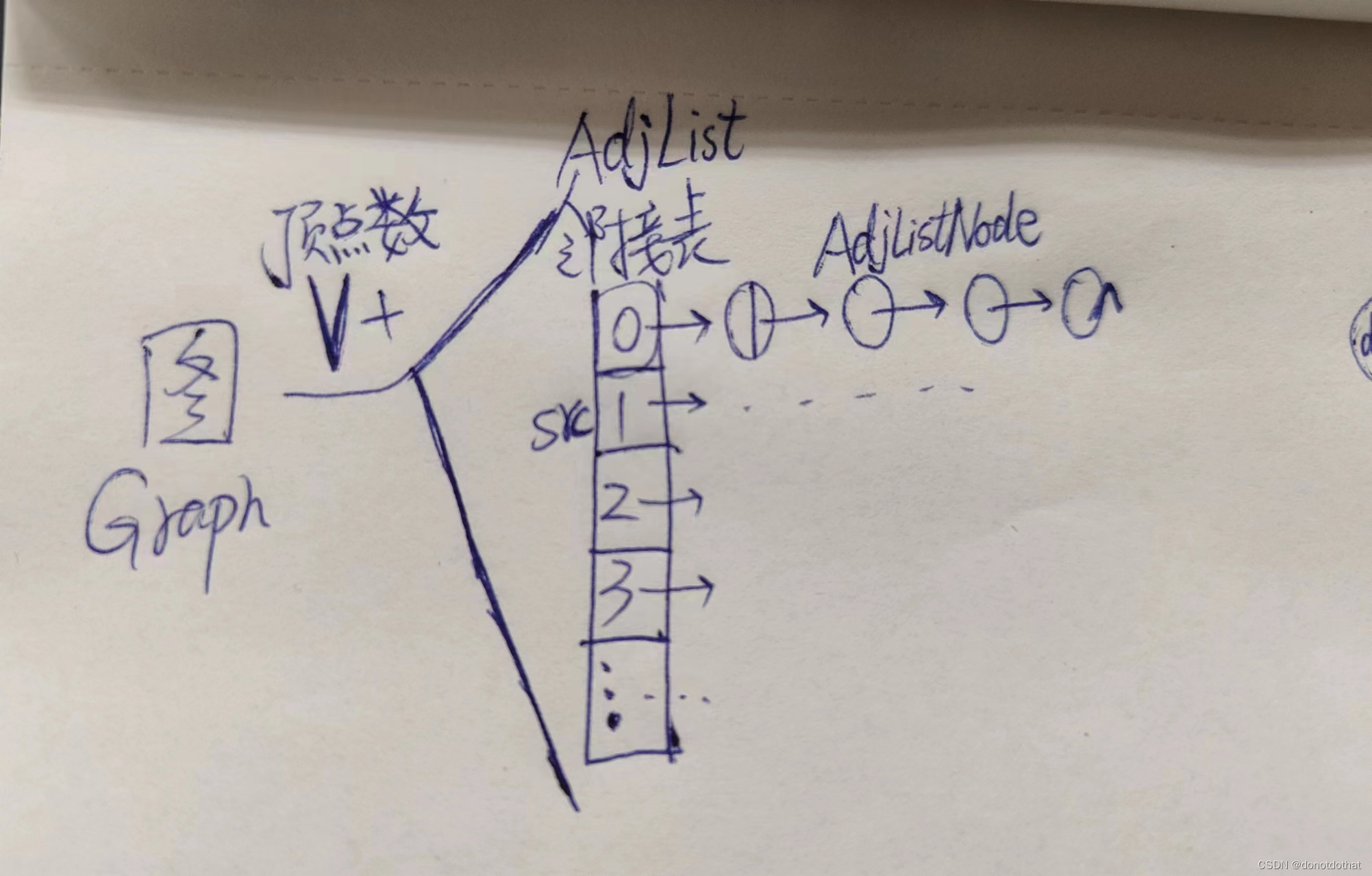
-
邻接表的每个结点中的数据域dest是顶点的编号,也就是和该顶点src有关系的结点。比如src = 1,1->3->4->6->2; 就表示src1的所有邻接点为:dest3、dest4、dest6、dest2。
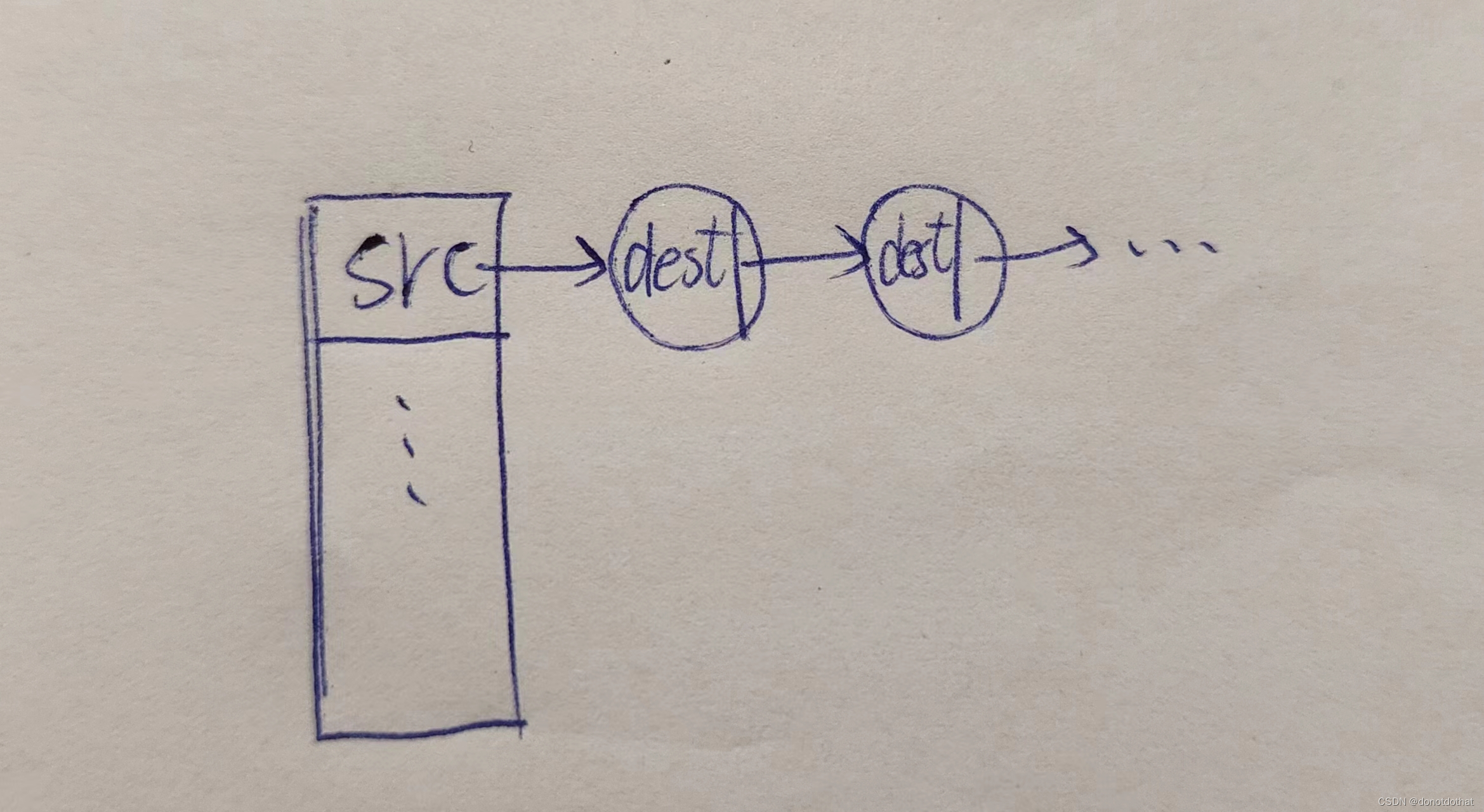
-
创建没有边的图:像邻接矩阵一样,先是创建一个没有边的图。在邻接矩阵中,没有边的图表现为所有元素为0。在这里,就是初始化邻接表的头结点head指向NULL,也就是每一个顶点后边跟着的那个链表都是空的。
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V; // 设置图的顶点数量
// 创建V个邻接表
graph->array = (struct AdjList*)malloc(V * sizeof(struct AdjList));
// 初始化每个邻接表的头节点为NULL
for (int i = 0; i < V; ++i) {
graph->array[i].head = NULL;
}
- 添加边到图:插入边的过程就是将和该顶点有关系的其他顶点插入到特定邻接表head之后的过程。每个array[i]邻接表插入边的过程就类似于一条单链表不断插入新的节点的过程:
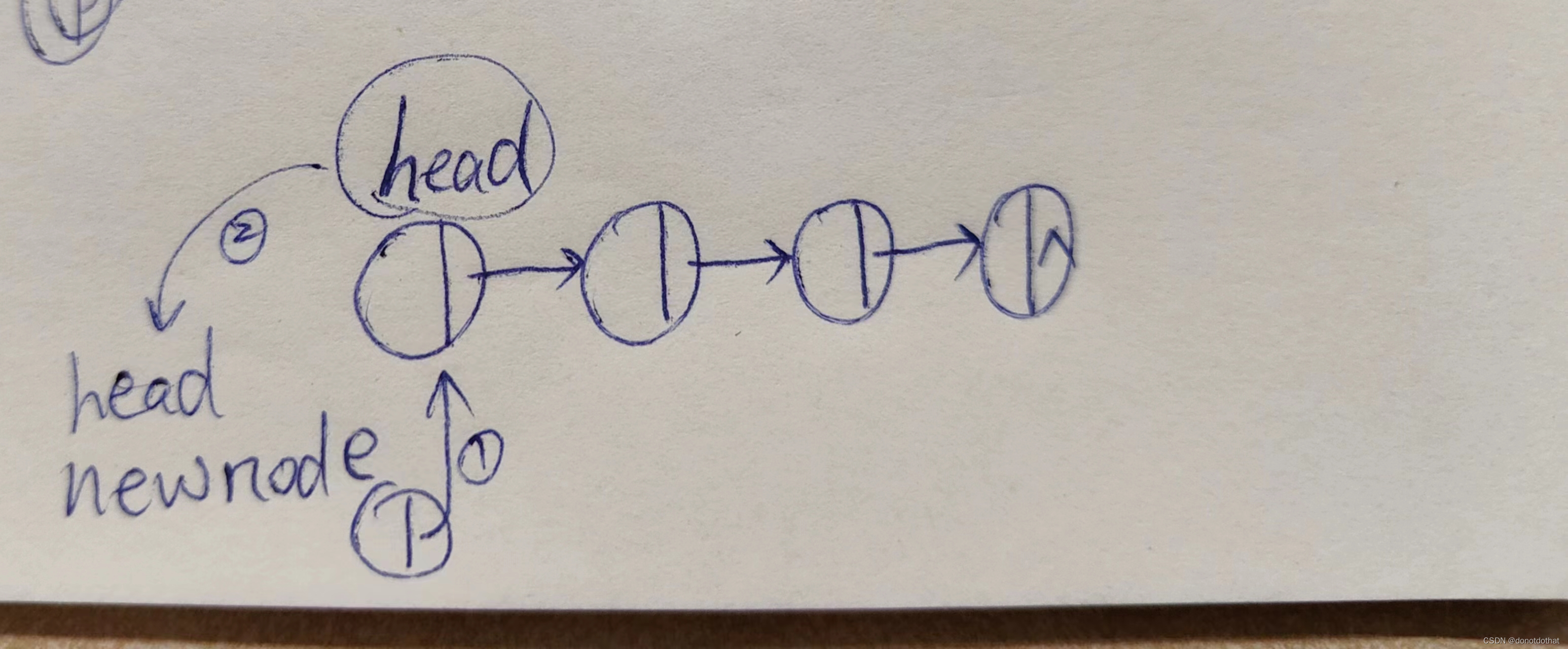
如果是无向图,如果首次插入的是V1->V2的边,那么紧跟着对应插入V2->V1这条边。
// 添加从src到dest的边
struct AdjListNode* newNode = newAdjListNode(dest);
newNode->next = graph->array[src].head; // 将新节点的下一个指针指向当前的头节点
graph->array[src].head = newNode; // 将头节点更新为新节点
//再添加从dest到src的边
newNode = newAdjListNode(src);
newNode->next = graph->array[dest].head; // 将新节点的下一个指针指向当前的头节点
graph->array[dest].head = newNode; // 将头节点更新为新节点
5.图的遍历
把图中的结点都访问一遍,而且不能有重复的访问。
5.1深度优先搜索 DFS
(Depth First Search)
深度优先搜索的过程类似迷宫点灯,起点开始点灯,每一步都将当前的灯点亮。如果视野范围内的灯全都亮了,就原路返回,直到原路返回到原来的起点,才能够保证所有的灯都已经点亮。
注意使用Visit[V] = true来记录顶点已经被访问过了,检查条件设置为if( !Visit[V] ),无需重复访问。
原路返回这种行为,在程序中对应堆栈的出栈。
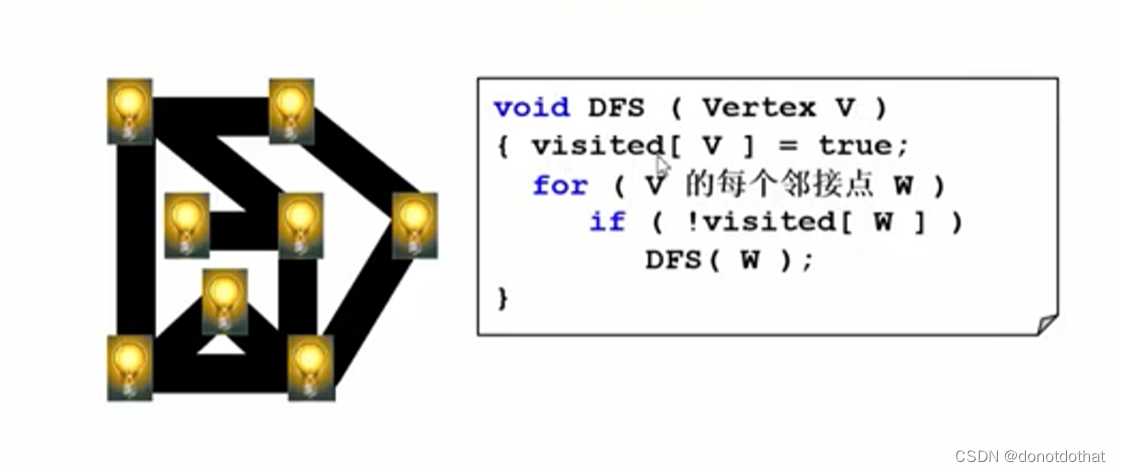
- 从某一个顶点作为起点开始,将此顶点的灯点亮(变为true),开始对他的所有邻接点逐一递归,如果有没点亮的,本层DFS()等待,对邻接点DFS点亮;如果所有的顶点都点亮了,逐一开始回溯,返回上一层。
- 整个DFS递归的过程类似于树的先序遍历。
- 对于邻接表表示的图,因为整个遍历对每个节点和每条边(即对应的邻接点)都访问了一次,时间复杂度是
O(N+E).节点数+边数(邻接点数) 。因为邻接表表示的图,每条链表上的节点都是对应顶点与之有连接的。 - 对于邻接矩阵表示的图,因为具体不知道一个特定顶点和哪些顶点存在边,所以还是要访问对应顶点的一整行,确定和谁有边的联系,哪个是他的邻接点并查看是否点亮,时间复杂度是
O(N的平方)
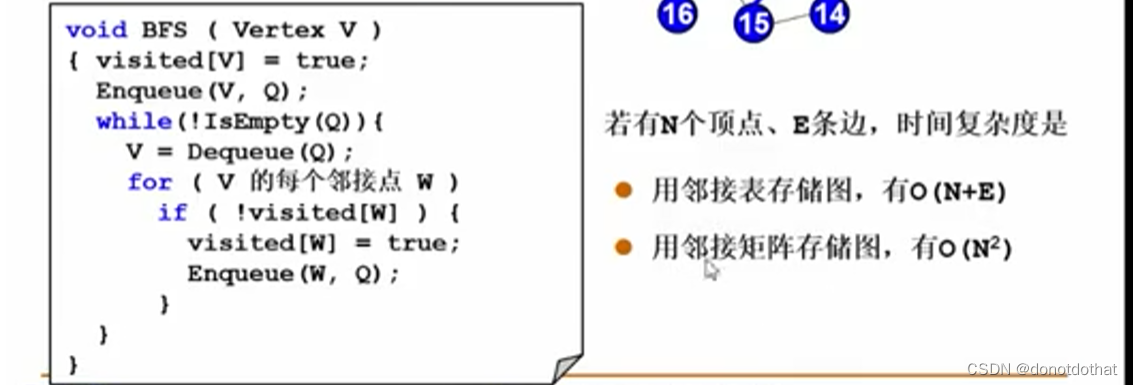
5.2广度优先搜索 BFS
(Breadth First Search)
图的广度优先搜索其实就类似于树的层序遍历,使用队列。
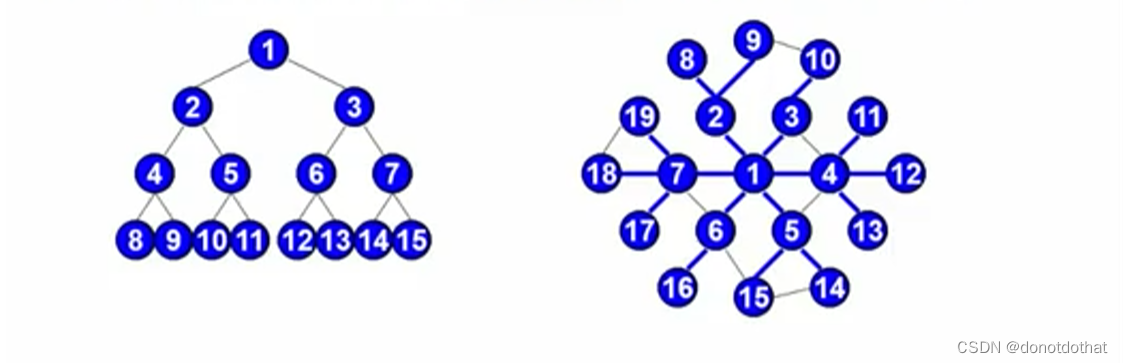
- 先访问图的起点顶点,将它入队列,开始循环:访问并弹出当前节点,将它的邻接点入队列;访问队列中下一个顶点、出队,并且将该顶点的邻接点入队…
- 使用邻接表存储图,对每个顶点以及对应的边数(即邻接点)都访问一次,时间复杂度是
O(N+E); - 使用邻接矩阵储存图,对每个顶点都访问了一次,在寻找某个顶点的邻接点的时候是比较费事的,对于每一个顶点都要遍历矩阵对应的一整行,时间复杂度是
O(N的平方)。
5.3为什么需要两种遍历?
所谓遍历,不过是将图中的每个顶点访问一次。其实两种遍历都有自己的特点。
以迷宫为例,
将白格子认为是走得通的,黑格子是走不通的。每个白格子可以看做是图上的每一个顶点,相邻的两个白格子之间可以认为是邻接点的关系,也就是边。
DFS:

- 从起点顶点开始,依次从上方开始顺时针检查米字格(八个方位),遇到可以走的(也就是邻接点),就前进;一直走到全都不通或者已经走过就返回;直到找到出口。
- 深入探索:它会尽可能深入子节点,直到不能再深入为止,然后回溯。
- 不保证最短路径:DFS找到的路径不一定是最短路径。
BFS:
从起点顶点开始,先将起点入队列,开始:访问并出队,将出队白格子的所有相邻白格子(所有邻接点)入队;继续访问队列并出队,将此顶点的所有相邻白格子入队…
广度优先搜索其实是一圈一圈地进行广度搜索

- BFS可以保证找到从起点到终点的最短路径(在未加权图中)。
- 速度较慢:在深度较大的图中,BFS可能比DFS更慢。
5.4图不连通怎么办?
无向图
- Part1

所谓简单路径,就是路径上所有的顶点都不是相同的;一旦存在相同的顶点,就说明这个路径是存在闭环回路的,那就不是简单路径。
- Part2
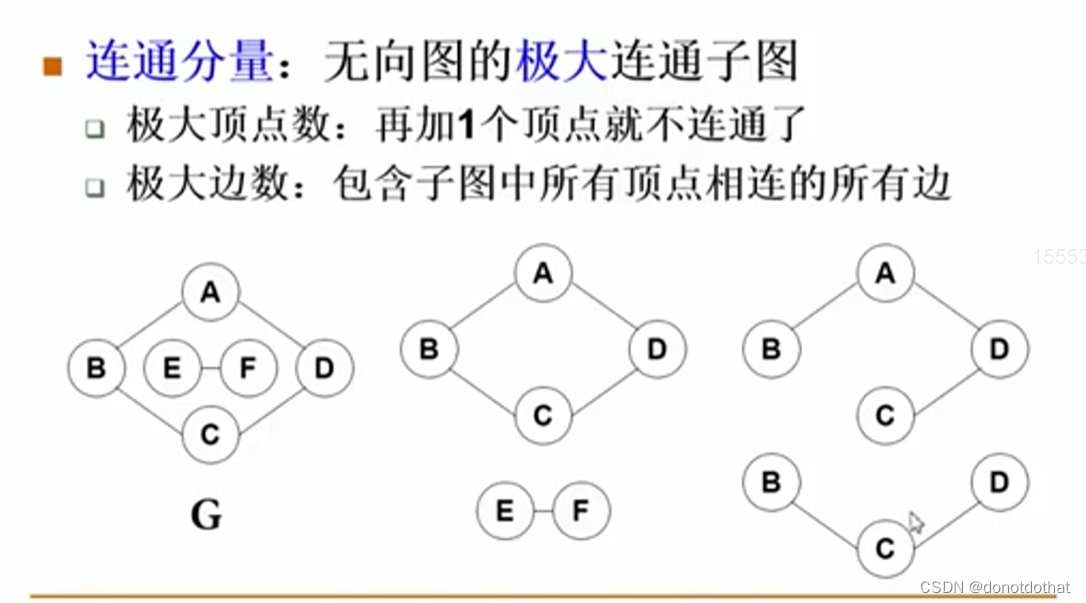
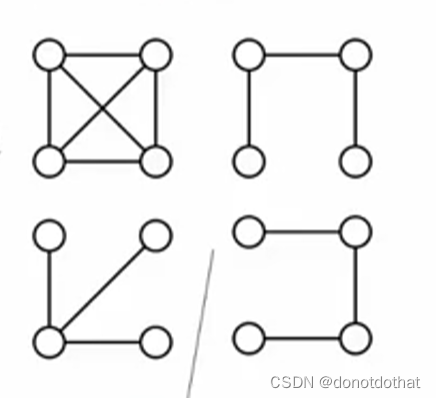
连通分量:无向图中的极大连通的子图。这里的极大包括两方面:有极大的顶点数和极大的边数。
所谓子图,就是包含了一个图的部分边和部分顶点。
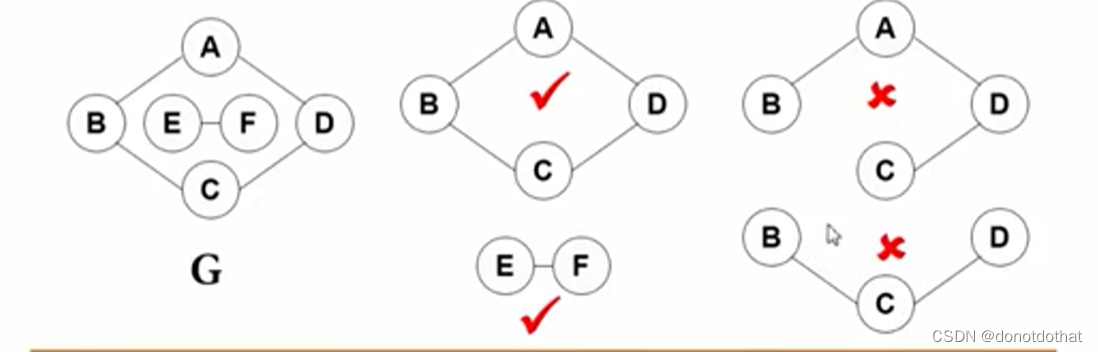
就像在这个例子中,左边的这俩子图都是联通分量,如果再加任一顶点就不连通了并且包含相连顶点的所有边。
有向图
- Part1

与强连通相对的,弱连通满足:不满足强连通的条件,但是将边的方向去掉之后,可以变成一个连通的无向图。
- Part2
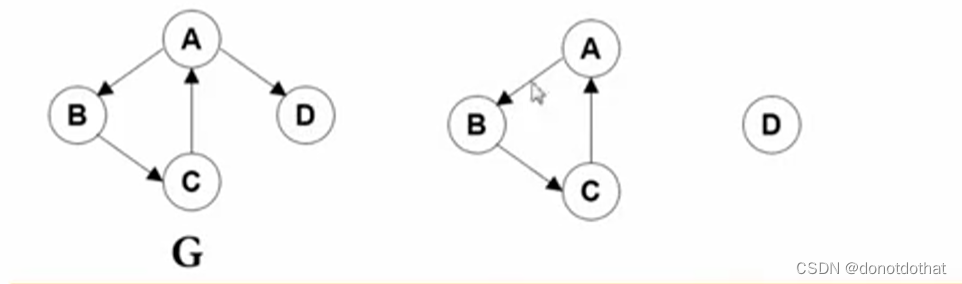
在有向图G中,右边两个子图都是强连通分量。ABC三个顶点之间任意两个顶点之间都存在双向路径。
当图不连通
每调用一次BFS(V) / DFS(V),其实就是把V所在的连通分量遍历了一遍。当存在孤立的好几个不同的连通分量时,需要分别遍历这几个连通分量
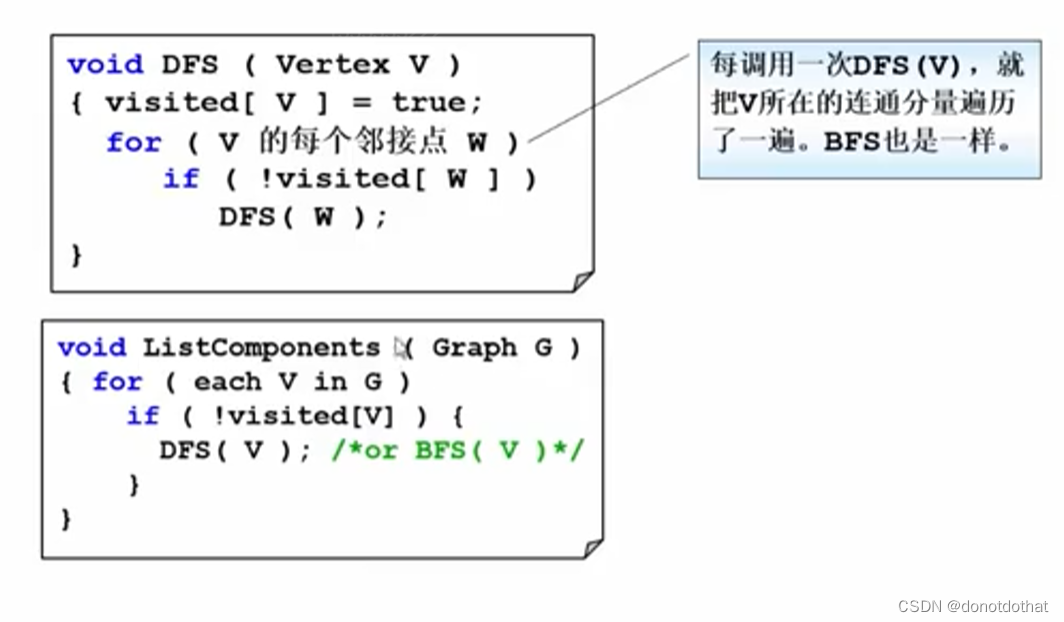
这样每当通过一个顶点V调用DFS,V所在的那个连通分量中所有的顶点都会被访问,使用Visit[v] = true来记录访问过的顶点,访问完所有顶点的时候,所有连通分量都会被访问。
5.5遍历代码
邻接表:更适合稀疏图和需要频繁遍历邻接节点的情况(如 DFS 和 BFS),因为它在遍历邻接节点时效率更高,一条链表储存的都是邻接点。
邻接矩阵:更适合密集图和需要频繁查找边的情况,因为对于需要频繁检查两顶点之间是否存在边的算法,邻接矩阵能提供更快的查询速度,直接if(G[V1][V2] == 1)
所以,通常情况下,深度优先搜索(DFS)和广度优先搜索(BFS)更适合使用邻接表来实现。
基于邻接表的 DFS
//深度优先搜索 算法
void DFS(Node** adjList, int vertex/*起点*/, int visited[]/*记录的数组*/) {
Node* adjListPtr = adjList[vertex]; // 获取当前顶点的邻接链表,就是该顶点的第一个邻接点
Node* temp = adjListPtr; // 临时指针用于遍历邻接链表
visited[vertex] = 1; // 标记当前顶点
printf("%d -> ", vertex); //访问, 打印当前顶点
// 遍历邻接链表
while (temp != NULL) {
int connectedVertex = temp->vertex; // 获取后边的邻接顶点
// 如果邻接顶点未被访问,则递归进行DFS
if (visited[connectedVertex] == 0) {
DFS(adjList, connectedVertex, visited);
}
temp = temp->next; // 移动到下一个邻接节点
}
}
整个while循环结束后,作为起点的顶点vertex那条邻接表链表上所有邻接点都已经被访问过,并且由该邻接表上的每个邻接点为接口,分别进行了DFS深度优先搜索。也就是说,只需要对起点所在的一条链进行,最后循环结束时所有的顶点都已经完成了访问。
基于邻接表的 BFS
// 广度优先搜索算法
void BFS(Node* adjList[]/*表明是储存着指针的数组*/, int startVertex/*起点*/, int visited[]) {
Queue* q = createQueue(); // 创建一个队列
visited[startVertex] = 1; // 标记起点顶点为已访问
enqueue(q, startVertex); // 将起始顶点加入队列
while (!isEmpty(q)) {
int currentVertex = dequeue(q); // 从队列中取出一个顶点
printf("%d -> ", currentVertex); // 访问,打印当前顶点
Node* temp = adjList[currentVertex]; // 获取当前顶点的邻接链表的第一个邻接点
// 遍历邻接链表
while (temp) {
int adjVertex = temp->vertex; // 获取邻接顶点,vertex就是顶点编号部分!
// 如果邻接顶点未被访问,则标记为已访问并加入队列
if (visited[adjVertex] == 0) {
visited[adjVertex] = 1;
enqueue(q, adjVertex);
}
temp = temp->next; // 移动到下一个邻接节点
}
}
}
将起点顶点入队、标记,开始循环:出队、打印(访问)、遍历该顶点的邻接表 若未访问就入队、二轮循环继续出队…
每出队一个起点顶点的邻接点,就将此邻接点的所有邻接点入队;一层一层向外搜索;
对比两种遍历
- DFS:深入搜索,标记起始顶点为已访问,并处理该顶点,对于当前顶点的每个邻接顶点,如果该顶点未被访问,则递归地进行深度优先搜索;
- BFS:广度搜索,一圈一圈地向外扩展,标记起始顶点为已访问,处理该顶点,将该顶点的所有邻接点都入队,继续出队,重复操作;
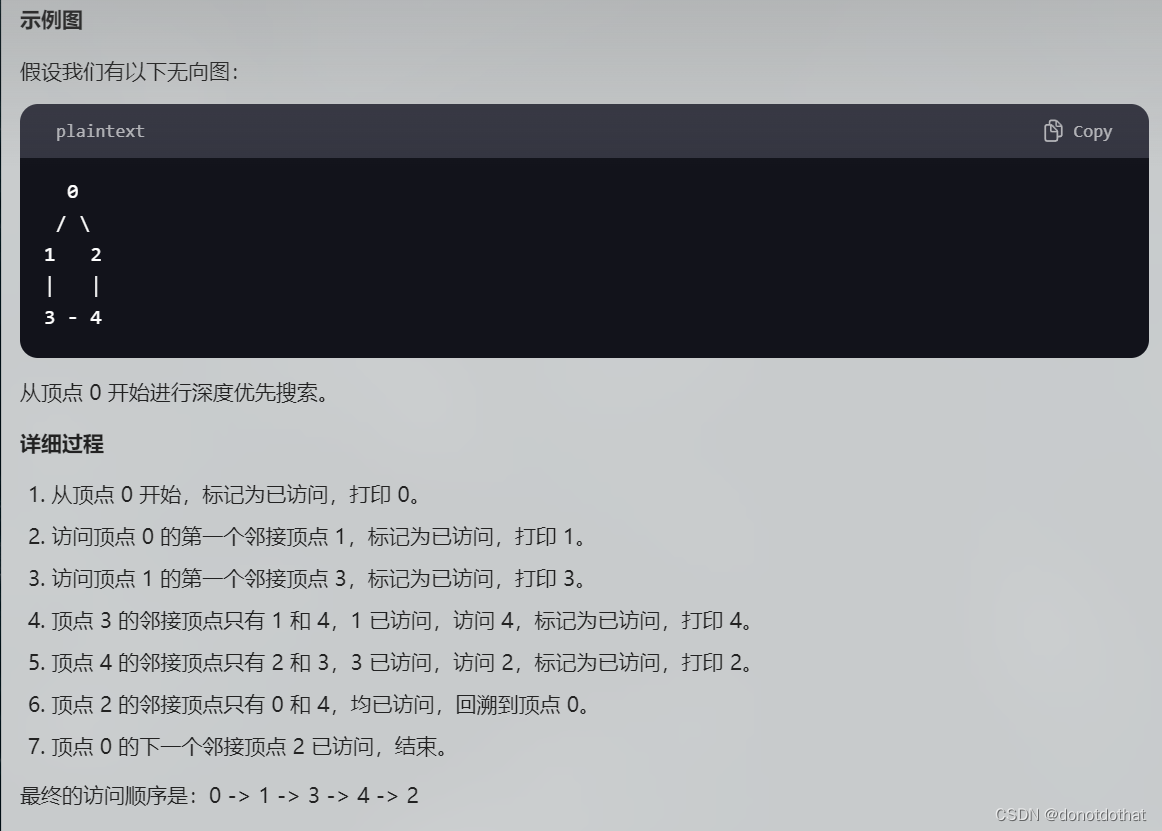
这个示例图采用BFS:

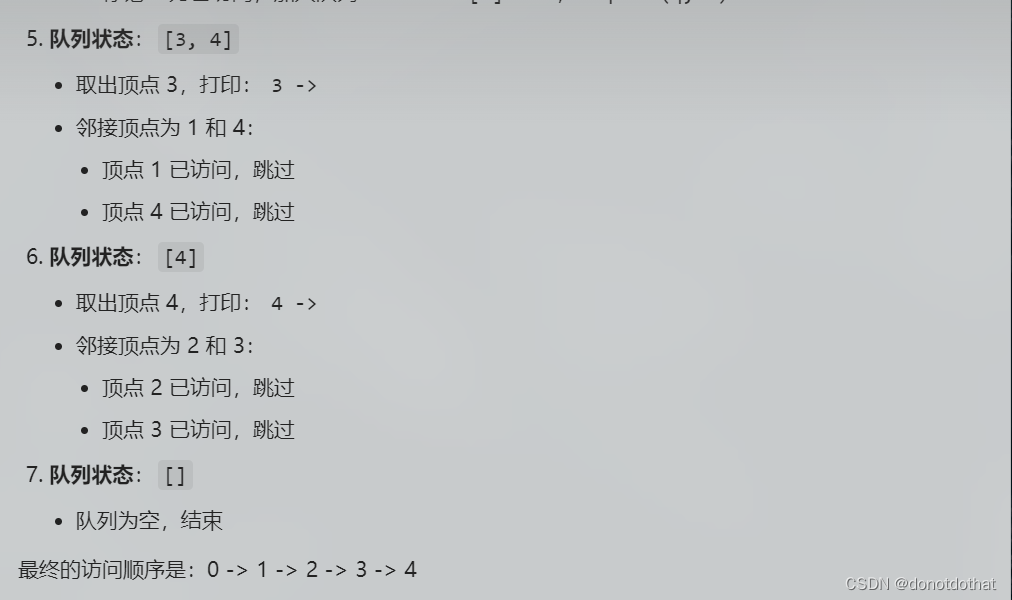
在代码中,类似adjList[src]的语句是顶点 src 的邻接链表的头节点,即顶点 src 的第一个邻接点。它不表示顶点 src 本身,而是作为第一个邻接点链接一个链表,链表中的每个节点代表顶点 src 的邻接点。在一个顶点的邻接表中添加边,就是在链表中添加邻接点结点!
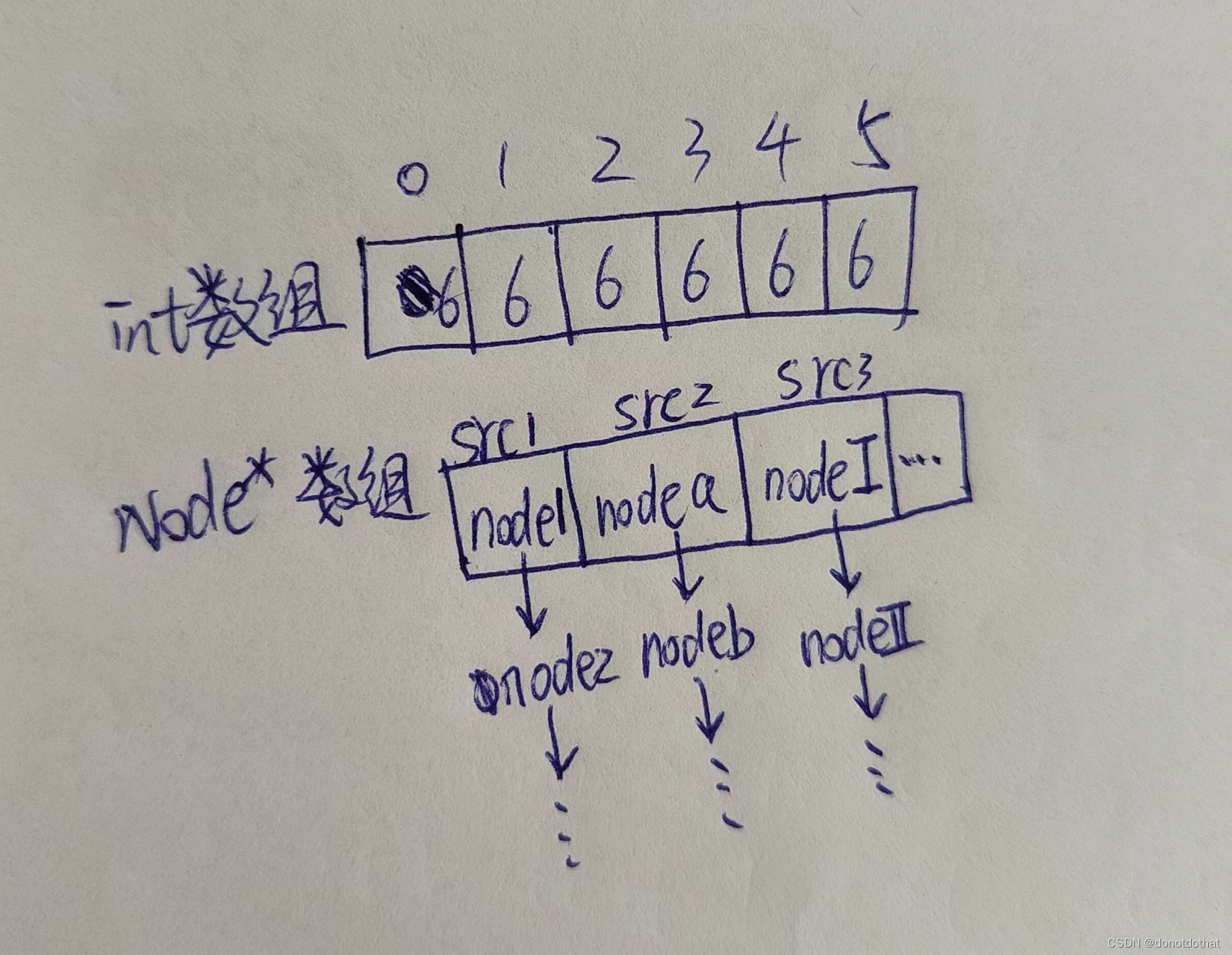
每个顶点都有自己的邻接表,储存邻接点。顶点编号src就像是下标索引一样,不是储存在数组中的具体元素!上图中adjList[src1]就指的是node1,就像常见的普通数组一样a[0] 指的就是 6 。
6.最小 生成 树(MST)
Minimum Spanning Tree
6.1定义
- 是一棵树。树是特殊的图,一定是连通的且没有回路;如果有v个顶点,那么一定就有v-1条边。
- 是生成树。它一定包含图上的全部顶点,它有的v-1条边在图里是存在的。
- 边的权重和最小。
- 充分必要条件:最小生成树存在
<->图是连通的。 - 生成树是不唯一的,向生成树中任加一条边都一定构成回路。
最小生成树是一个连通无向图的子图,最小生成树是否唯一,取决于图中边的权重是否唯一。如果图中存在多条权重相同的边,那么最小生成树可能不唯一。
6.2贪心算法
解决最小生成树问题有不同的算法,都可以归结为贪心算法。
“贪”:一步一步解决问题,解决问题的过程中每一步都要最好的,只要眼前最好的。“好”:每次都要一条权重最小的边。
约束:
- 只能用图上有的边
- 只能正好用掉v-1条边,不多也不少
- 一定不能有回路
在满足约束的条件下,使用贪心算法。
6.3Prim算法 —让一棵小树长大
针对顶点
比如,这个图,从v1开始,使用Prim算法找到最小生成树:
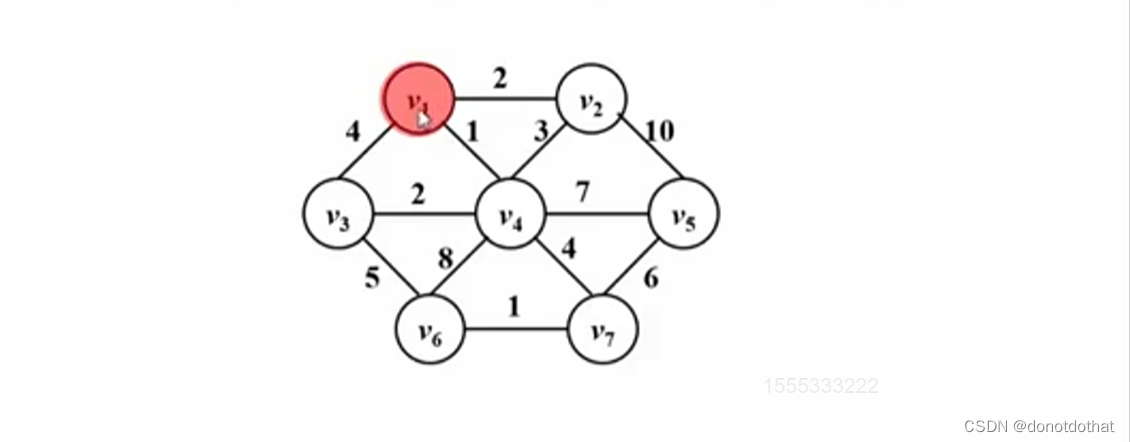
- 从v1开始,找一条最小权重的边,收入v4,构成了包含v1和v4的树;
- 继续找最小权重的边,收入v2,构成了包含v1、v4和v2的树;
- 继续找,收入v3,构成了包含v1、v4、v2和v3的树;
- …重复操作,注意过程中不能生成回路!
- 最后的树就是最小生成树:
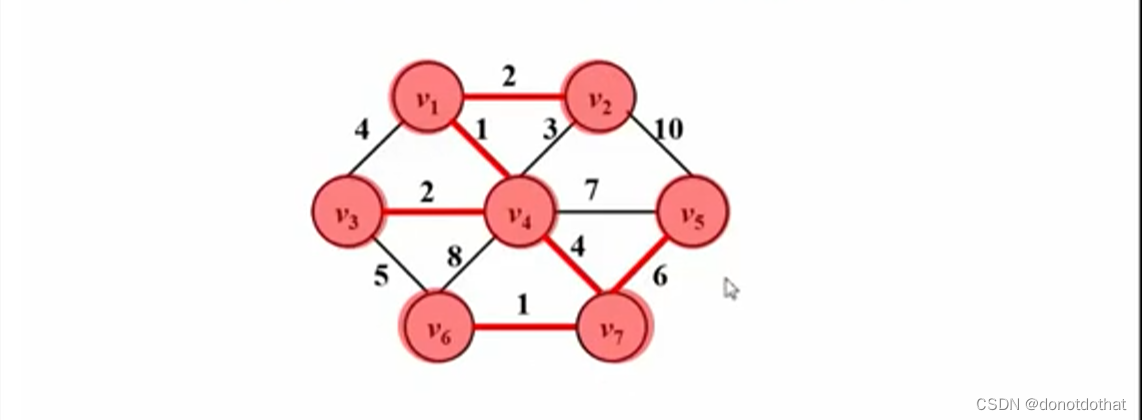
注意图中一共有7个顶点,那么就说明最后的最小生成树一定是7-1=6条边,包括完整的7个顶点。
伪代码

- 一开始选择根节点s。
- 这里的dist定义成一个顶点v到这棵最小生成树的距离。如果一个顶点和根节点s有边相连,也就是v和s之间是连通的话,就定义dist[v] = E(s,v)二者之间的距离;如果v不是s的邻接点,就把dist[v] = 正无穷。
- 存一个节点的父节点parent[s] = -1;s就是根节点。
v = dist最小者;如果找到了这样的v,就将他收入到MST中:dist[v] = 0;收入进MST就表示成为了树的一部分,距离设置为0;- break之后会有两种情况:在连通图中,所有顶点都已经收入到MST中,完成了最小生成树的建立;另一种情况就是这个图本身就不是连通的,剩下的顶点到这这棵树之间的距离都是无穷大,所以最小生成树不存在。
Prime算法适用于处理稠密图
6.4Kruskal算法—把森林合并成树
针对边
直截了当的贪心,每次将权重最小的边收入树中
以下面的这个图为例:
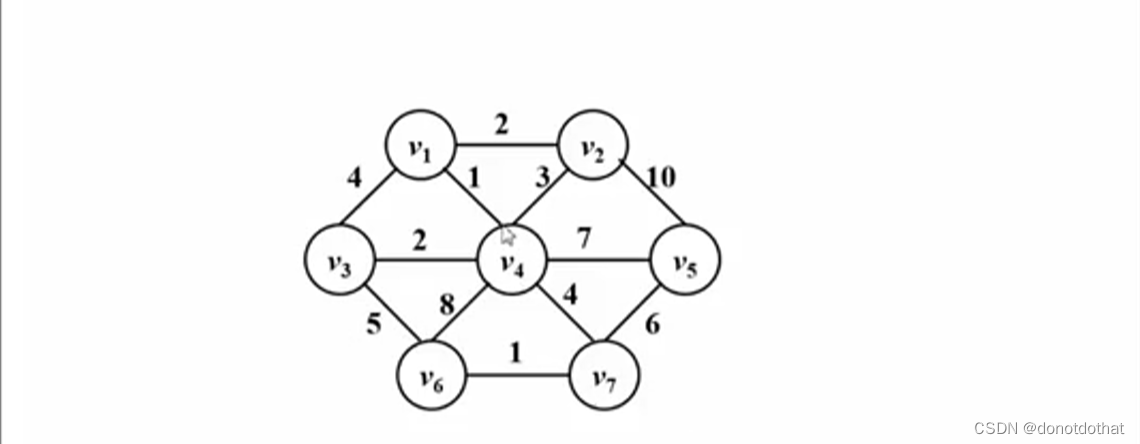
认为初始状态下,每一个顶点都是一棵树,通过不断找寻权重最小的边,就把两棵树合并成了一棵树,最终将7个节点并成整个一棵树。
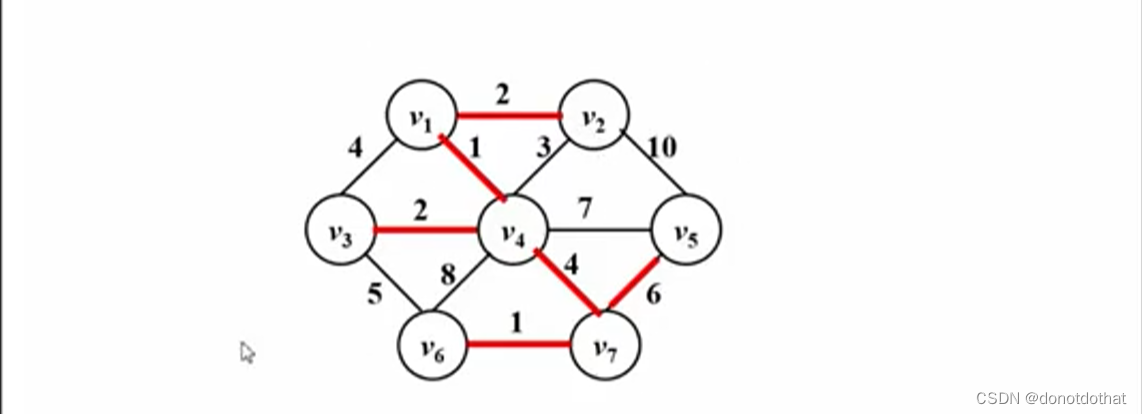
先后将1,1,2,2,4,6这几条边收入,建成最小生成树。一定要注意过程中不要形成回路!可以看到和Prime算法的结果是一样的。
伪代码
在Kruskal算法里,最小生成树收集的是边而不是顶点
E指的是图的边的集合;

使用到了最小堆(将E中边的权重排成一个最小堆)和并查集(同样是将两棵树合并成一棵树的思想,插入边合成之前看v和w是否已经在一棵树中。如果在同一棵树中,那么就会构成回路)。
当图是非常稀疏即顶点个数V和边数E是同一数量级的时候,时间复杂度就近似于 O(VlogV),比Prime的O(V的平方)要稍微快一些。
6.5拓扑排序 (AOV网络)
Activity On Vertex,每一个顶点代表一个事件或活动。
引例:计算机专业排课:
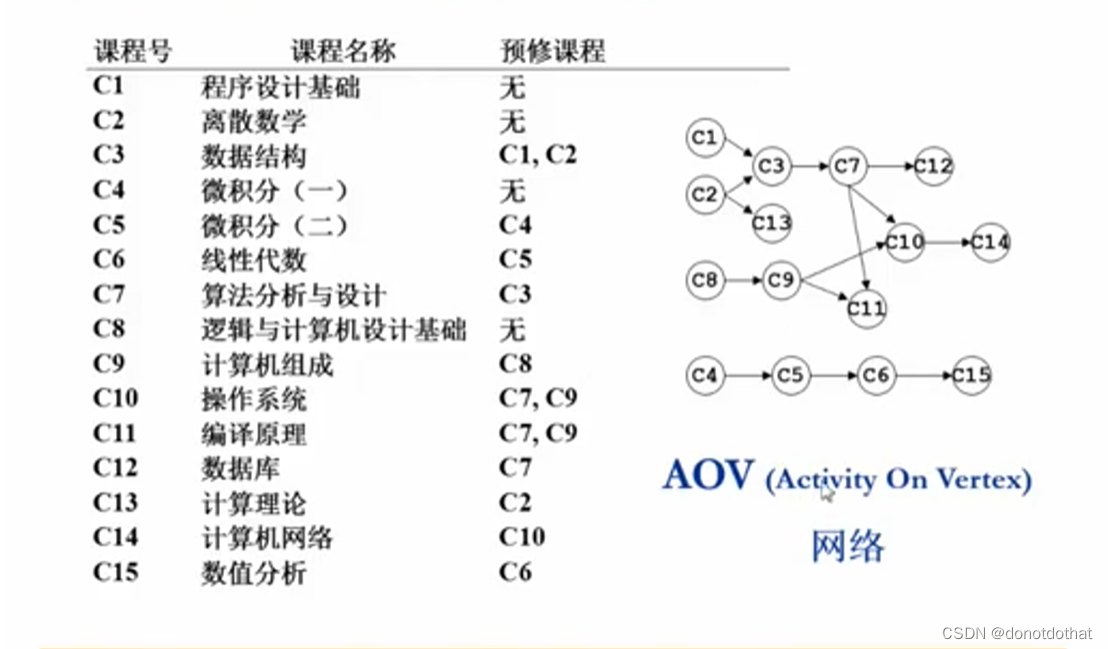
- 这个专业课的依赖关系图,叫做AOV网络。在这个有向图中,每一个顶点代表一个事件或活动。
所有的真实的活动都是表现在顶点上的,顶点和顶点之间的有向边表示了两个活动的先后顺序。
- 拓扑序:从v到w有一条有向路径,则v要在w之前输出(v要在w之前学,先输出v再输出w)

注意拓扑排序是基于有向图,并且必须没有闭合回路(无环)!!
- 根据输出的先后顺序,就得到了拓扑排序:

从前向后输出的是没有前驱顶点的顶点,也就是说,入度 = 0 的顶点。每一次选择的都是入度为0的顶点,在输出的同时要把这个顶点从原来的图中彻底“抹掉”;当图中的所有顶点都已经抹光的时候,拓扑排序就完成了。
- 程序1
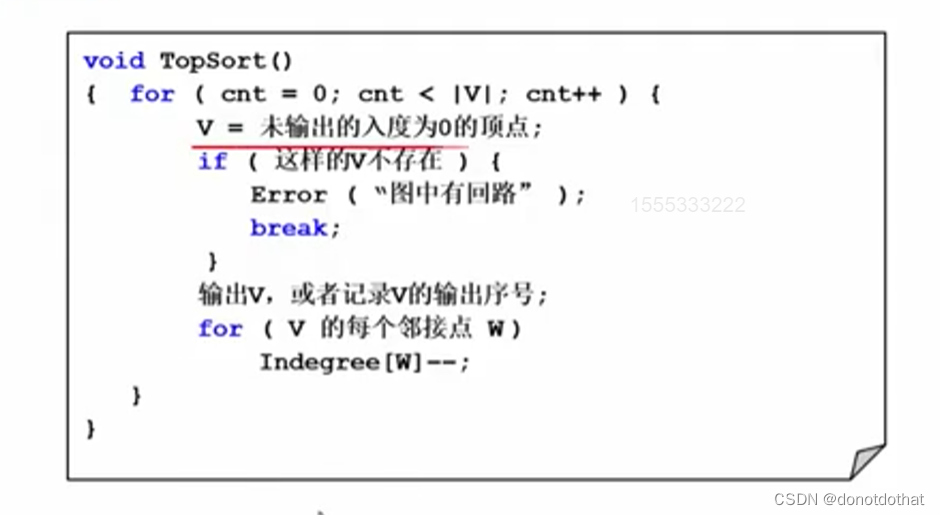
所谓“抹掉”顶点v,就是对于v的所有邻接点w,将w的入度-1即可。
如果循环没有达到预设的V次,而找不到满足条件的V了,那么就表示图中必定存在回路,无法进行拓扑排序。
- 优化程序
如何查找未输出的、入度为0的顶点就决定了算法的时间复杂度。
- 如果采用简单暴力的算法,即每次循环都去搜索一遍未输出的入度为0的顶点,那么时间复杂度就是
O(V的平方); - 效率更高的算法就是,随时将入度变为0的顶点放到一个容器里(这个容器可以是数组、链表、堆栈、队列等)。一开始原本是有度为0的顶点的,随着抹去一个一个的顶点,对应的邻接点的度就会减少,那么度为0的顶点就会增加。这样到下一次要找一个度为0的顶点的时候,就不用去扫描所有现存的顶点的集合了,直接到容器里面取一个出来就好:

使用一个队列来储存入度=0的顶点,首先对原始的情况进行一次顶点遍历判断,将入度= 0的结点入队;接着进行while循环,不断将入度为0的顶点抹去,同时出队(因为没有用了);对于出队顶点的影响—相应邻接点的入度-1,紧跟着判断邻接点的入度,变成0的入队(因为影响到的只有出队顶点的邻接点,只要判断邻接点即可);增加一个计数器,以便于在while循环结束(即队列为空)之后再判断是否完成了拓扑排序。
- 优化后的时间复杂度是
O(V+E),如果是稀疏图:O(V);如果是稠密图:近似为O(V的平方)。 - 这个程序还可以检测有向图是否是一个有向无环图。
6.6关键路径 (AOE网络)
1.Activity On Edge
每一个边代表一个事件或活动。
1 活动表示在边上,有上下两块区域,持续时间和机动时间;
2 每一个顶点分成三块,顶点编号、最早完成时间和最晚完成时间。
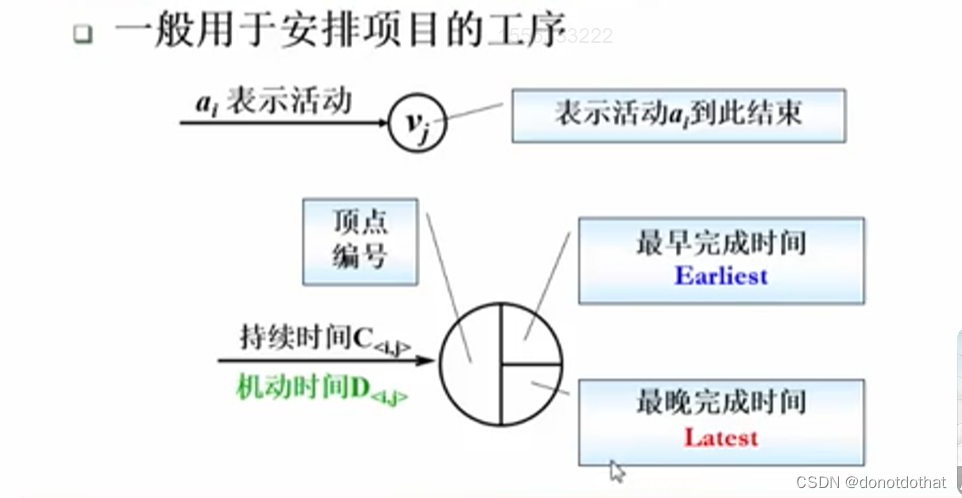
-
例子:
工期:最早完成时间正推;选择最大的时间,蓝字是前一条边(前一个的活动)最早完成的时间、下一个活动的最早开工时间;
机动时间:倒推;选择最小的时间,红字是下一条边(下一个活动)的最晚开工时间、上一个活动的最晚完成时间;
机动时间绿字,就是工期不紧,可以调出去干别的事;机动时间 = 最晚完成时间-最早开工时间-时间耗费
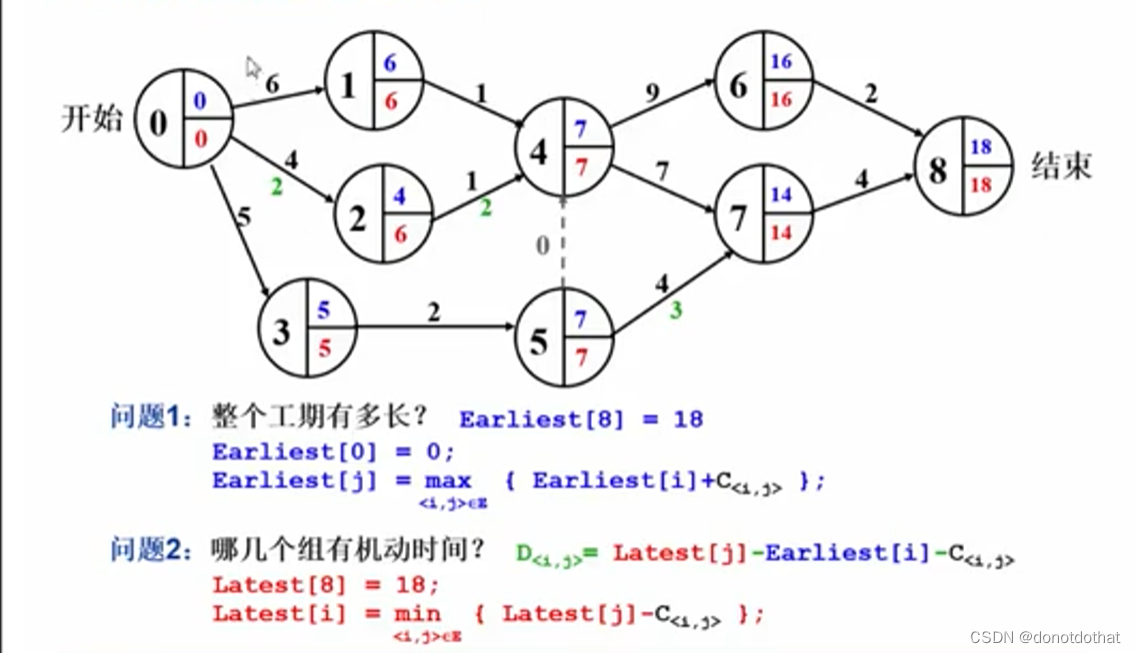
-
那什么是关键路径呢?
关键路径就是哪个事件是最不能耽误的,只要他耽误一天,整个工期都要耽误。即由绝对不允许延误的活动组成的路径。就是机动时间为0的活动从头走到尾组成的路径,可以不止一条。