正态性检验
正态性检验的目的是确定一组数据是否符合正态分布(也称高斯分布)。在统计分析和数据建模中,正态性假设是许多统计方法和模型的基础。了解数据是否符合正态分布有助于选择适当的统计方法和确保分析结果的有效性。
本文主要从概率统计方面来进行正态性检验。即假设检验的角度来说,数据是否服从正态分布可以通过与“数据服从正态分布”这样一个零假设进行假设检验计算,构建相关统计量来计算出检验结果。文中提及的Q-Q Plot是描述性统计方法。
先把这篇好文章放在开头!!!
正态检验 (Normality Test)——常见方法汇总与简述-CSDN博客文章浏览阅读5.5w次,点赞89次,收藏374次。前 言在科学研究中,往往需要对数据进行差异性检验,而常用的参数检验需要数据服从正态分布,因此在决定是否采用参数检验之前需要先对数据进行正态性检验。这一步在任何统计学软件中(如SPSS、SAS、Origion、GraghPad等)都能够轻易实现,但每个软件都会同时包括多种正态检验方法,此时该选哪个方法来对自己的数据进行正态性检验呢?这就是本文要解决的主要问题。在查阅相关资料后,本文将对多种常见的正态检验方法进行简单地归纳总结,尽可能写清楚每个检验方法的适用范围,但对于每个检验方法的数学统计学原理不作深入解_正态检验https://blog.csdn.net/qq_33924470/article/details/114668701
正态性检验的目的
-
验证正态性假设:
- 许多统计方法(如 t 检验、ANOVA、回归分析)假设数据来自正态分布。正态性检验可以帮助确认这些假设是否合理。
-
指导统计方法的选择:
- 如果数据符合正态分布,可以使用参数统计方法,这些方法在正态性假设下更有效。
- 如果数据不符合正态分布,应该使用非参数统计方法,这些方法不依赖于正态性假设。
-
识别数据特征:
- 正态性检验可以揭示数据的分布特征,如偏态和峰态,这对于数据预处理和特征工程很重要。
正态性检验的意义
-
确保分析的准确性:
- 确保使用的统计方法适用于数据,避免因不合理的假设导致错误的结论。
-
提高模型性能:
- 符合正态分布的数据在许多机器学习和统计模型中表现更好,正态性检验帮助识别和处理偏离正态分布的数据。
-
数据预处理:
- 正态性检验结果可以指导数据变换(如对数变换、平方根变换),使数据更符合正态分布,优化模型性能。
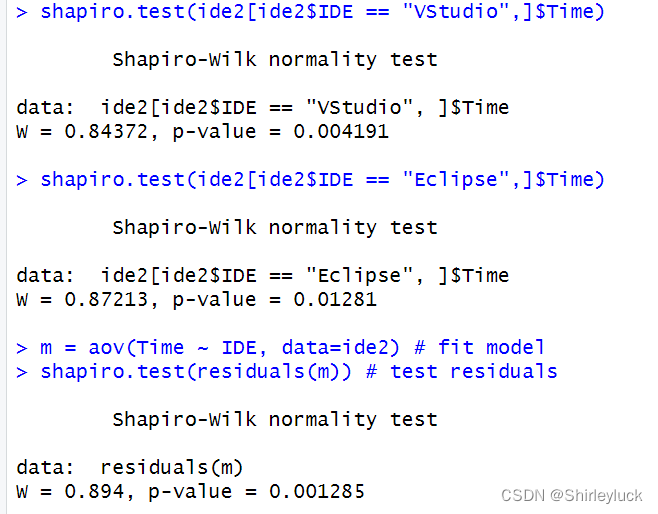
上图中,shapiro.test 函数用于进行Shapiro-Wilk正态性检验,以确定数据是否来自正态分布。使用 shapiro.test 检验了 ide2 数据框中 IDE 为 "VStudio" 的 Time 列,。
示例
shapiro.test(ide2[ide2$IDE == "VStudio",]$Time)
Shapiro-Wilk normality test
data: ide2[ide2$IDE == "VStudio", ]$Time
W = 0.84372, p-value = 0.004191
结果解释
- W 值: Shapiro-Wilk检验的统计量。值接近1表明数据接近正态分布,值较小则表明偏离正态分布。
- p-value: 用于判断数据是否符合正态分布的显著性水平。
- 如果 p-value > 0.05,表示无法拒绝原假设,即数据可能来自正态分布。
- 如果 p-value ≤ 0.05,表示拒绝原假设,即数据显著偏离正态分布。
本次的结果中:
- W = 0.84372: W 值表明数据可能存在偏离正态分布的情况。
- p-value = 0.004191: p-value 小于 0.05,表示数据显著偏离正态分布。
进一步步骤
-
非参数检验:由于数据不符合正态分布,可以考虑使用非参数检验方法,比如 Mann-Whitney U 检验(也称为 Wilcoxon 秩和检验)来比较不同组别的数据。
-
数据变换:尝试对数据进行变换(如对数变换或平方根变换)以使其更接近正态分布,然后重新进行正态性检验。

常用的正态性检验方法
-
Shapiro-Wilk Test:
- 用于小样本数据(n < 50)。
- 例子:
shapiro.test(data)
-
Kolmogorov-Smirnov Test:
- 用于大样本数据。
- 例子:
ks.test(data, "pnorm", mean=mean(data), sd=sd(data))
-
Anderson-Darling Test:
- 对尾部更敏感。
- 需要额外的包,例如
nortest。 - 例子:
library(nortest); ad.test(data)
-
Q-Q Plot (Quantile-Quantile Plot):
- 通过图形方法直观检查数据是否符合正态分布。
- 例子:
qqnorm(data); qqline(data)
shapiro.test 函数会自动选择合适的方法进行正态性检验(这也太方便了吧)。通常情况下,它会根据数据样本的大小来选择适当的统计方法。
在 R 中,shapiro.test 函数主要使用 Shapiro-Wilk 检验来进行正态性检验。Shapiro-Wilk 检验对于样本量较小(一般小于 50)的情况较为适用。对于较大的样本量,该函数可能会使用其他方法,但是这些细节通常是隐藏的,不需要用户来指定。
当调用 shapiro.test 函数时,你只需要提供要进行正态性检验的数据,函数会自动选择适当的方法并返回检验结果,包括统计量和 p 值。
能否指定检验方法呢?
要指定使用特定的检验方法,需要使用其他的正态性检验函数,例如 ad.test、lillie.test、cvm.test 等。以下是一些常见的正态性检验方法及其相应的函数:
概率统计(假设检验角度):
- Shapiro-Wilk Test:
shapiro.test - Anderson-Darling Test:
ad.test(需要加载额外的包,如nortest) - Lilliefors Test:
lillie.test(需要加载额外的包,如nortest) - Cramér-von Mises Test:
cvm.test(需要加载额外的包,如goftest)
# 加载 nortest 包
library(nortest)
# 使用 Anderson-Darling 正态性检验
ad.test(data)
# 使用 lillie.test 函数进行 Lilliefors 正态性检验
lillie.test(data)
# 加载 goftest 包
library(goftest)
# 使用 cvm.test 函数进行 Cramér-von Mises 正态性检验
cvm.test(data)
描述性统计:
m = aov(Time ~ IDE, data=ide2) # fit model
shapiro.test(residuals(m)) # test residuals
qqnorm(residuals(m)); qqline(residuals(m)) # plot residuals其中aov用于拟合方差分析模型。为了评估方差分析模型(ANOVA)假设的正态性,使用qqnorm和qqline绘制 Q-Q 图。
Q-Q 图(Quantile-Quantile Plot)是一种图形方法,用于比较数据的分布与正态分布。如果数据点大致沿着一条直线分布,则数据可以被认为是正态分布的。