PyTorch中的模型创建

最全最详细的PyTorch神经网络创建~

话不多说直接开始~

神经网络的创建步骤

定义模型类，需要继承nn.Module
定义各种层，包括卷积层、池化层、全连接层、激活函数等等
编写前向传播，规定信号是如何传输的

可以用 torchsummary 查看网络结构，如果没有的话，使用pip命令进行安装

Module: 神经网络的模板

import torch.nn as nn
import torch.nn.functional as F

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1,20, 5)
        self.conv2 = nn.Conv2d(20, 50, 5)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        return  F.relu(self.conv2(x))

神经网络中常见的各种层

常见的层包括：卷积层，池化层，全连接层，正则化层，激活层

导入层有两种方法：

一种是将其看作一个类，在torch.nn里面

另一种是将其看作一个函数，在torch.nn.functional里面可以调用

全连接层

全连接层又称为线性层，所以函数名叫 Linear，执行的操作是𝑦=𝑥𝐴𝑇+𝑏

torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)

in_feature代表输入数
out_features代表输出数，即神经元数量

m = nn.Linear(2,3)
input = torch.randn(5, 2)
ouput = m(input)
print(ouput.size())

输出：torch.Size([5, 3])

先搭建个只有一层的网络，用 torchsummry 查看网络结构

from torch import nn
from torchsummary import summary
class NeuralNetwork( nn . Module):
    def _init_( self) :
        super()._init___()
        self.fc = nn.Linear(10,1，bias=False)# 如果 bias=True（默认），则有11个参数
def forward(self, x):
    x = self.fc(x)
    return x
if _name_ == '_main__':
    network = NeuralNetwork()# print( network)
    summary ( network，(10,))

自定义输入到网络中，得到输出

import torch
from torch import nn
from torchsummary import summary
class NeuralNetwork ( nn.Module):
    def _init_( self):
        super()._init___()
        self.fc = nn.Linear( 10,1)
    def forward(self,x ):
        x = self.fc(x)
        return x
if _name_ == '_main_':
    network = NeuralNetwork()

    input = torch.randn(10)
    print("input = " ,input)
    output = network( input)
    print( "output = ", output)
    result = output. detach( ) .numpy()
    print( "result = " , result)

多个 FC 层之间可以连接起来

class NeuralNetwork( nn.Module) :
    def _init_( self):
        super()._init_()
        self.fc_1 = nn.Linear ( 1000, 100)
        self.fc_2 = nn.Linear ( 100,10)
        self.fc_3 = nn.Linear( 10,5)
    def forward( self，x):
        ×= self.fc_1(x)
        ×= self.fc_2(x)
        x= self.fc_3(x)
        return x

激活函数

常见的激活函数包括 sigmoid，relu，以及softmax

Sigmoid

sigmoid是早期的激活函数

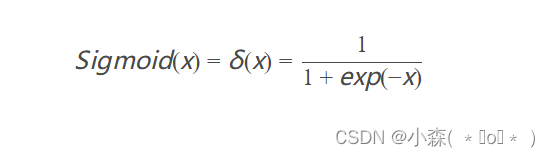
将所有值压缩到0-1之间

ReLU

ReLU激活函数常放在全连接层、以及卷积层后面

调用方法都放在 nn.ReLU()

Softmax

softmax是在分类当中经常用到的激活函数，用来放在全连接网络的最后一层，Softmax函数通常用于多类分类问题的输出层，将输出转换为概率分布的形式。

import torch
import torch.nn as nn
m=nn.Softmax( dim=1)
input = torch.randn(4，3)
output = m( input)

nn.softmax的dim参数表示在哪个维度上进行softmax操作。默认值为1，表示在输入张量的第二个维度（即列）上进行softmax操作。

随机失活方法Dropout

当 FC层过多，容易对其中某条路径产生依赖，从而使得某些参数未能训练起来

为了防止上述问题，在 FC层之间通常还会加入随机失活功能，也就是Dropout层

它通过在训练过程中随机失活一部分神经元，从而增强模型的泛化能力。

m=nn.Dropout( p=0.5)
input = torch.randn(6，8)
output = m( input)

将一个列表，随机将一些值变为0

全连接网络处理一维信息

搭建以上的网络结构，组合全连接层，dropout层，激活函数，我们就可以构建出一个完整的全连接网络结构：

import torch
from torch import nn
from torchsummary import summary
class NeuralNetwork( nn.Module):
    def _init_( self):
        super()._init_()
        self.relu = nn.ReLU()
        self.softmax = nn.softmax(dim=1)
        self.dropout = nn.Dropout(0.5)
        self.fc_1 = nn.Linear(1000, 100)
        self.fc_2 = nn.Linear(100,10)
        self.fc_3 = nn.Linear(10, 5)
    def forward(self, x):
        x = x.view(-1，1000)# view的存在，可以自动适应batchsize
        x = self.dropout( self.relu( self.fc_1(x) ) )
        x = self.dropout( self.relu( self.fc_2(x) ) )
        x= self.softmax ( self.fc_3(x))
        return x

全连接网络处理二维图像

使用全连接网络处理二维图像信息，当二维特征（Feature Map）转为一维特征时，需要从高维压缩成一维，这时候可以用 tensor.view()，或者用nn.Flatten(start_dim=1)

import torch
import torch.nn as nn

# 创建一个输入张量
input_tensor = torch.randn(2, 3, 4)

# 创建Flatten层
flatten_layer = nn.Flatten(start_dim=1)

# 对输入张量进行展平操作
output_tensor = flatten_layer(input_tensor)

print("Input Tensor:")
print(input_tensor)
print("Output Tensor:")
print(output_tensor)



# 输出
Input Tensor:
tensor([[[-0.5968, -0.0790,  0.0597, -0.2250],
         [ 0.1564, -0.1564, -0.0790, -0.1564],
         [-0.1564, -0.1564, -0.1564, -0.1564]],

        [[ 0.1564, -0.1564, -0.1564, -0.1564],
         [-0.1564, -0.1564, -0.1564, -0.1564],
         [-0.1564, -0.1564, -0.1564, -0.1564]]])
Output Tensor:
tensor([[-0.5968, -0.0790,  0.0597, -0.2250,  0.1564, -0.1564, -0.0790, -0.1564],
        [-0.1564, -0.1564, -0.1564, -0.1564, -0.1564, -0.1564, -0.1564, -0.1564]])

卷积层

二维卷积

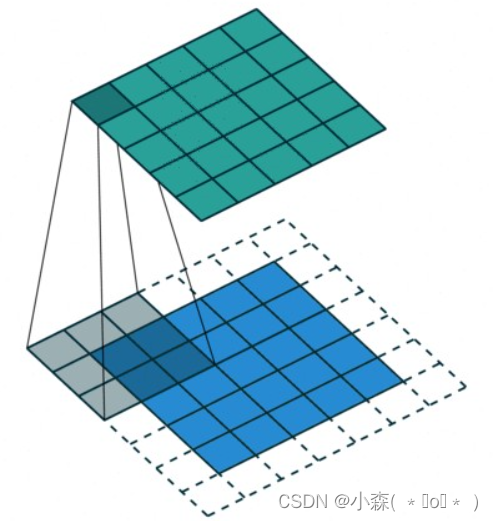
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode=‘zeros’, device=None, dtype=None)

in_channels: 输入通道数
out_channels: 输出通道数（卷积核数量）
kernel_size: 卷积核大小
stride: 卷积步长
padding: 边缘补零
dilation: 扩散卷积
group: 分组卷积
bias: 是否带有偏置

import torch
import torch.nn as nn
#使用方形卷积核，以及相同的步长
m = nn.conv2d(16，33，3, stride=2)
#使用非方形的卷积核，以及非对称的步长和补零
m = nn.conv2d(16，33，(3，5),stride=(2，1)，padding=(4，2))
#使用非方形的卷积核，以及非对称的步长，补零和膨胀系数
m = nn.Conv2d(16，33，(3，5)，stride=(2，1)，padding=(4，2)，dilation=(3，1))
input = torch.randn(20，16，50，100)
output = m( input)
print(output.shape)

转置卷积就是卷积的逆操作，也称为逆卷积、反卷积

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode=‘zeros’, device=None, dtype=None)

输入：(𝑁,𝐶𝑖𝑛,𝐻𝑖𝑛,𝑊𝑖𝑛)或者(𝐶𝑖𝑛,𝐻𝑖𝑛,𝑊𝑖𝑛)
输出：(𝑁,𝐶𝑜𝑢𝑡,𝐻𝑜𝑢𝑡,𝑊𝑜𝑢𝑡)或者(𝐶𝑜𝑢𝑡,𝐻𝑜𝑢𝑡,𝑊𝑜𝑢𝑡)

转置卷积是一种卷积神经网络中的操作，它的作用是将输入的特征图进行上采样，从而增加特征图的尺寸。转置卷积通常用于生成器网络中，将低分辨率的图像转换为高分辨率的图像。

import torch
import torch.nn as nn

# 定义一个转置卷积层
transposed_conv = nn.ConvTranspose2d(in_channels=3, out_channels=64, kernel_size=4, stride=2, padding=1)

# 创建一个输入张量，形状为 (batch_size, in_channels, height, width)
input_tensor = torch.randn(1, 3, 32, 32)

# 使用转置卷积层处理输入张量
output_tensor = transposed_conv(input_tensor)

print("输入张量的形状：", input_tensor.shape)
print("输出张量的形状：", output_tensor.shape)

搭建全卷积网络结构案例

import torch.nn as nn
import torch.nn.functional as F
import torch
from torchsummary import summary

class FCN(nn.Module):
    def __init__(self,num_classes):
        super(FCN,self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=3).cuda()  # kernel_size=3, 卷积核大小
        self.conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3).cuda()
        self.conv3 = nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3).cuda()

        self.upsample1 = nn.ConvTranspose2d(in_channels=128, out_channels=64, kernel_size=3).cuda()
        self.upsample2 = nn.ConvTranspose2d(in_channels=64, out_channels=32, kernel_size=3).cuda()
        self.upsample3 = nn.ConvTranspose2d(in_channels=32, out_channels=num_classes, kernel_size=3).cuda()
        # 最后的upsample3 输出通道数和标签类别一致

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = F.relu(self.upsample1(x))
        x = F.relu(self.upsample2(x))
        x = F.relu(self.upsample3(x))
        return  x

# 10个类别的图像分割
num_classes = 10
# 每个像素都会得到一个10维的特征向量，表示它属于每个类别的概率
fcn_model = FCN(num_classes)

print(fcn_model)
summary(fcn_model, (3, 224, 224))

输出：

FCN(
  (conv1): Conv2d(3, 32, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1))
  (conv3): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1))
  (upsample1): ConvTranspose2d(128, 64, kernel_size=(3, 3), stride=(1, 1))
  (upsample2): ConvTranspose2d(64, 32, kernel_size=(3, 3), stride=(1, 1))
  (upsample3): ConvTranspose2d(32, 10, kernel_size=(3, 3), stride=(1, 1))
)
----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1         [-1, 32, 222, 222]             896
            Conv2d-2         [-1, 64, 220, 220]          18,496
            Conv2d-3        [-1, 128, 218, 218]          73,856
   ConvTranspose2d-4         [-1, 64, 220, 220]          73,792
   ConvTranspose2d-5         [-1, 32, 222, 222]          18,464
   ConvTranspose2d-6         [-1, 10, 224, 224]           2,890
================================================================
Total params: 188,394
Trainable params: 188,394
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 121.57
Params size (MB): 0.72
Estimated Total Size (MB): 122.86
----------------------------------------------------------------

搭建卷积+全连接的网络结构

import torch.nn as nn
import torch.nn.functional as F
import torch
from torchsummary import summary

class ConvNet(nn.Module):
    def __init__(self,num_classes=10):
        super(ConvNet,self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=3).cuda()  # kernel_size=3, 卷积核大小
        self.conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3).cuda()

        # 全连接层
        self.flatten = nn.Flatten(start_dim=1).cuda()
        # 将输入张量从第1个维度开始展平
        self.fc1 = nn.Linear(64*28*28, 50).cuda()
        # 输入图像的大小为64x28x28,输出特征数为50
        self.fc2 = nn.Linear(50, num_classes).cuda()
        # 输入特征数为512，输出特征数为num_classes

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.flatten(x)
        x = self.fc1(x)
        x = self.fc2(x)
        return  x

# 10个类别的图像分割
num_classes = 10
# 每个像素都会得到一个10维的特征向量，表示它属于每个类别的概率
conv_net = ConvNet(num_classes)

bacth_size = 4
input_tensor = torch.randn(bacth_size, 3, 32, 32).cuda()    # 输入是4张32x32的RGB图像
output = conv_net(input_tensor)

print(output.shape)
summary(conv_net, (3, 32, 32))

输出：

torch.Size([4, 10])
----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1           [-1, 32, 30, 30]             896
            Conv2d-2           [-1, 64, 28, 28]          18,496
           Flatten-3                [-1, 50176]               0
            Linear-4                   [-1, 50]       2,508,850
            Linear-5                   [-1, 10]             510
================================================================
Total params: 2,528,752
Trainable params: 2,528,752
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.01
Forward/backward pass size (MB): 0.99
Params size (MB): 9.65
Estimated Total Size (MB): 10.64
----------------------------------------------------------------

Process finished with exit code 0

池化层

池化包含最大池化和平均池化，有一维池化，二维池化，三维池化，在这里以二维池化为例

最大池化就是求一个区域中的最大值，来代替该区域。

torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)

输入参数 kernel_size，stride，padding，dilation可以是

一个 int ：代表长宽使用同样的参数
两个int组成的元组：第一个int用在H维度，第二个int用在W维度

#长宽一致的池化，核尺寸为3x3，池化步长为2
m1 = nn.MaxPool2d( 3，stride=2)
#长宽不一致的池化
m2 = nn.MaxPool2d(( 3，2), stride=(2，1))
input = torch.randn(4，3，24，24)
output1 = m1( input)
output2 = m2(input)
print( "input.shape = " ,input.shape)
print( "output1.shape = ", output1.shape)
print( "output2.shape = " , output2.shape)

input.shape = torch.size( [4，3，24，24])

output1.shape = torch.size([4，3，11，11])

output2.shape = torch.size([4，3，11，23])

平均池化

平均池化就是用一个区域中的平均数来代替本区域

torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)

import torch
import torch.nn as nn
#长宽一致的池化,核尺寸为3x3，池化步长为2
m1 = nn.AvgPool2d( 3, stride=2)
#长宽不一致的池化
m2 = nn.AvgPool2d((3，2), stride=(2，1))
input = torch.randn( 4，3，24，24)
output1 = m1( input)
output2 = m2(input)
print( "input.shape = " , input. shape)
print( "output1.shape = ", output1.shape)
print( "output2.shape = " , output2.shape)

input.shape = torch.size([4，3，24，24])

output1.shape = torch.size([4，3，11，11])

output2.shape = torch.size([4，3，11，23])

BN层

BN，即Batch Normalization，是对每一个batch的数据进行归一化操作，可以使得网络训练更稳定，加速网络的收敛。

#批量归一化层（具有可学习参数)
m_learnable = nn.BatchNorm2d( 100)
#批量归一化层（不具有可学习参数>
m_non_learnable = nn.BatchNorm2d(100，affine=False)
#随机生成输入数据
input = torch.randn(20，100，35，45)
#应用具有可学习参数的批量归一化层
output_learnable = m_learnable( input)
# 应用不具有可学习参数的批量归一化层
output_non_learnable = m_non_learnable(input)
print( "input.shape = ", input.shape)
print( "output_learnable.shape = ", output_learnable.shape)
print( "output_non_learnable.shape = ", output_non_learnable.shape)

input.shape = torch.size( [20，100，35，45])
output_learnable.shape = torch.size( [20，100，35，45])

output_non_learnable.shape = torch.size([20，100，35，45])