Hw6 聚类
- 1
- a
- b
- 2
- a
- b
- c
- d
- 3
- a
- b
- c
- d
- e
- 4
- 5
- 6
- 7
- 8
- 9
1
a

b
一个点不来自某个特定簇的概率是
1
−
1
K
1-\frac{1}{K}
1−K1
对所有
2
K
2K
2K 个点都不来自该簇的概率是
(
1
−
1
K
)
2
K
(1-\frac{1}{K})^{2K}
(1−K1)2K
则 至少一个点来自该簇的概率为
1
−
(
1
−
1
K
)
2
K
1-(1-\frac{1}{K})^{2K}
1−(1−K1)2K
所以最终样本至少包含来自每个簇的一个点的概率是
(
1
−
(
1
−
1
K
)
2
K
)
K
(1-(1-\frac{1}{K})^{2K})^{K}
(1−(1−K1)2K)K
K
=
10
K=10
K=10 时,
p
=
0.27
p=0.27
p=0.27
K
=
100
K=100
K=100 时,
p
=
5.66
e
−
07
p=5.66e-07
p=5.66e−07
K
=
1000
K=1000
K=1000 时,
p
=
8.24
e
−
64
p=8.24e-64
p=8.24e−64
2
a
基于中心:2个簇,长方形区域会对半分。
基于邻近性:1个簇,因为有噪声
基于密度:2个簇,是2个圆形区域,噪声不会造成影响
b
基于中心:1个簇,包括了所有环
基于邻近性:2个簇,是2个环形区域
基于密度:2个簇,是2个环形区域
c
基于中心:3个簇,是3个三角形区域
基于邻近性:1个簇,三个三角形有交点因此会被合并
基于密度:3个簇,虽然它们有交点,但交点处密度低
d
基于中心:2个簇,左右各一个
基于邻近性:5个簇,每条线是一个簇
基于密度:2个簇
3
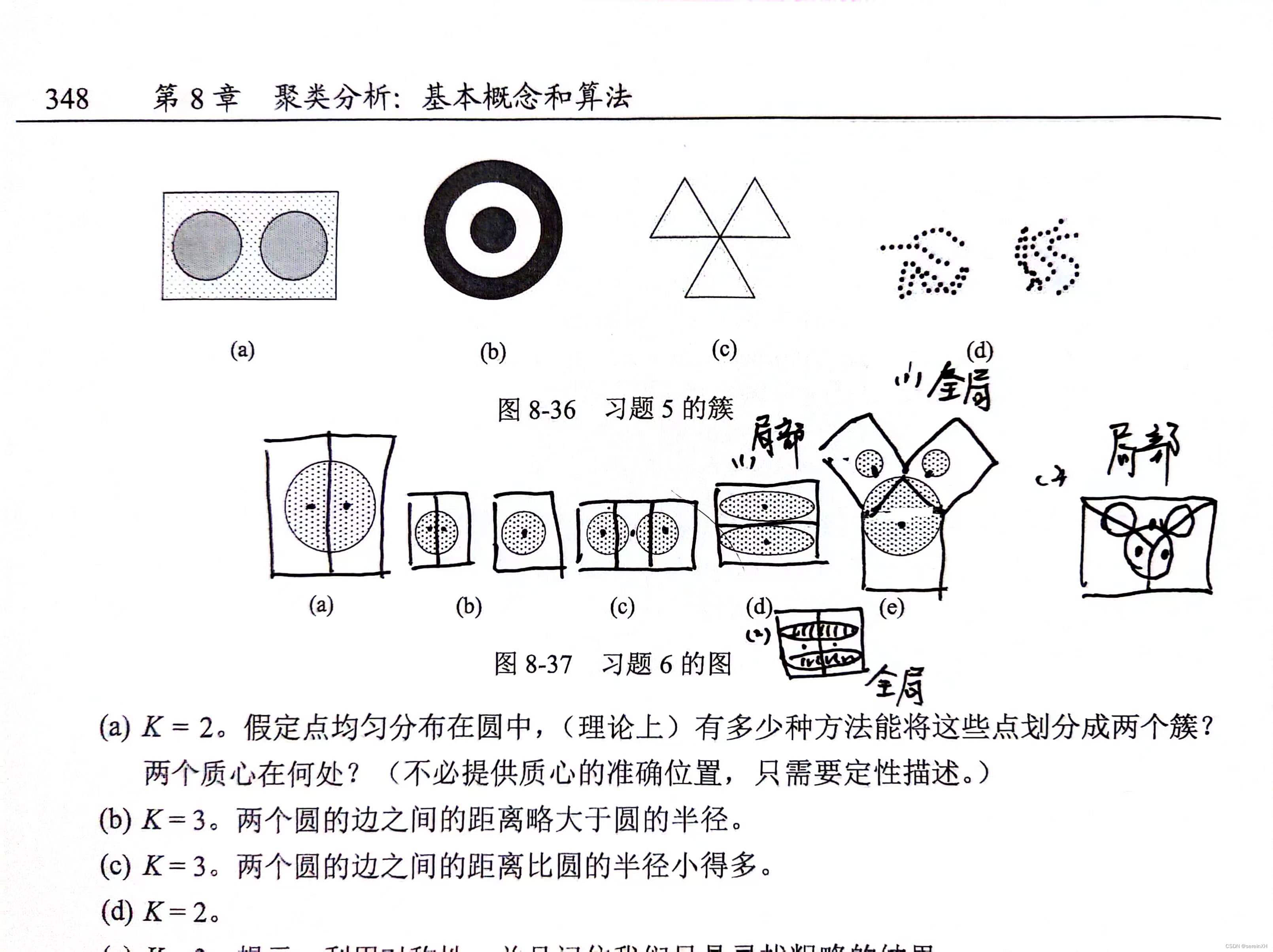
a
有无限种划分方法,任意一条直径即可
两个质心在该直径的垂直平分线上
是全局最小
b
从真实点作为初始质心开始,因为两个圆的边之间的距离略大于圆的半径,所以:将两个圆划分开,再用直径分割其中一个圆。
有无限种方法
两个半圆的质心同上一问,另一个是完整圆的中心
是全局最小
c
在初始质心是实际数据点的现实情况下,三个框显示了将导致的三个簇。
d
具体见图
在第一种情况下,这两个簇是局部最小。
在第二种情况下,这两个簇是全局最小。
e
具体见图,两个顶部簇被包含在两个框内,而第三个簇被三角形和矩形定义的区域包含。(图中较小的两个簇应为对称的。)我认为第二个解决方案——由一名学生提出——也是可能的,尽管它是一个局部最小值,在这种点的配置下可能很少见。注意,虽然从较大圆中切出的两个扇形被显示为相交于一点,但不一定是这种情况——这取决于圆的确切位置和大小。两个扇形切口之间可能存在一个间隙,由第三个(较大)簇填充。(想象小圆在相对两侧。)或者两个扇形切口之间的边界实际上可以是线段。
4
单链:

全链:

5
| 簇 | 熵 | 纯度 |
|---|---|---|
| #1 | 0.20 | 0.98 |
| #2 | 1.84 | 0.53 |
| #3 | 1.70 | 0.49 |
| 合计 | 1.44 | 0.61 |
6
相似度矩阵:
x
=
<
0.8
,
0.65
,
0.55
,
0.7
,
0.6
,
0.3
>
x=<0.8,0.65,0.55,0.7,0.6,0.3>
x=<0.8,0.65,0.55,0.7,0.6,0.3>
理想的相似度矩阵:
y
=
<
1
,
0
,
0
,
0
,
0
,
1
>
y=<1,0,0,0,0,1>
y=<1,0,0,0,0,1>
方差:
σ
x
=
0.1703
σ_x = 0.1703
σx=0.1703
σ
y
=
0.5164
σ_y = 0.5164
σy=0.5164
c o v ( x , y ) = − 0.2 cov(x,y) = -0.2 cov(x,y)=−0.2
c o r r ( x , y ) = c o v ( x , y ) σ x σ y = − 0.227 corr(x,y) = \frac{cov(x,y)}{ σ_xσ_y}= -0.227 corr(x,y)=σxσycov(x,y)=−0.227
7
- 簇1 {p1,p2,p3,p4,p5,p6,p7,p8}
- 类
A
A
A
R ( A , 1 ) = 3 3 = 1 R(A,1) = \frac{3}{3} = 1 R(A,1)=33=1
P ( A , 1 ) = 3 8 = 0.375 P(A,1) = \frac{3}{8} = 0.375 P(A,1)=83=0.375
F ( A , 1 ) = 2 × 1 × 0.375 1 + 0.375 = 0.55 F(A,1) = 2 × 1 ×\frac{0.375}{1+0.375} = 0.55 F(A,1)=2×1×1+0.3750.375=0.55 - 类
B
B
B
R ( B , 1 ) = 5 5 = 1 R(B,1) = \frac{5}{5} = 1 R(B,1)=55=1
P ( B , 1 ) = 5 8 = 0.625 P(B,1) = \frac{5}{8} = 0.625 P(B,1)=85=0.625
F ( B , 1 ) = 2 × 1 × 0.625 1 + 0.625 = 0.77 F(B,1) = 2 × 1 × \frac{0.625}{1+0.625} = 0.77 F(B,1)=2×1×1+0.6250.625=0.77
- 类
A
A
A
- 簇2 {p1,p2,p4,p5}
- 类
A
A
A
R ( A , 2 ) = 2 3 R(A,2) = \frac{2}{3} R(A,2)=32
P ( A , 2 ) = 2 4 P(A,2) = \frac{2}{4} P(A,2)=42
F ( A , 2 ) = 0.57 F(A,2) = 0.57 F(A,2)=0.57 - 类
B
B
B
R ( B , 2 ) = 2 5 R(B,2) = \frac{2}{5} R(B,2)=52
P ( B , 2 ) = 2 4 P(B,2) = \frac{2}{4} P(B,2)=42
F ( B , 2 ) = 0.44 F(B,2) =0.44 F(B,2)=0.44
- 类
A
A
A
- 簇3 {p3,p6,p7,p8}
- 类
A
A
A
R ( A , 3 ) = 1 3 R(A,3) = \frac{1}{3} R(A,3)=31
P ( A , 3 ) = 1 4 P(A,3) = \frac{1}{4} P(A,3)=41
F ( A , 3 ) = 0.29 F(A,3) = 0.29 F(A,3)=0.29 - 类
B
B
B
R ( B , 3 ) = 3 5 R(B,3) = \frac{3}{5} R(B,3)=53
P ( B , 3 ) = 3 4 P(B,3) = \frac{3}{4} P(B,3)=43
F ( B , 3 ) = 0.67 F(B,3) =0.67 F(B,3)=0.67
- 类
A
A
A
- 簇4 {p1,p2}
- 类
A
A
A
R ( A , 4 ) = 2 3 R(A,4) = \frac{2}{3} R(A,4)=32
P ( A , 4 ) = 2 2 P(A,4) = \frac{2}{2} P(A,4)=22
F ( A , 4 ) = 0.8 F(A,4) = 0.8 F(A,4)=0.8 - 类
B
B
B
R ( B , 4 ) = 0 5 R(B,4) = \frac{0}{5} R(B,4)=50
P ( B , 4 ) = 0 2 P(B,4) = \frac{0}{2} P(B,4)=20
F ( B , 4 ) = 0 F(B,4) =0 F(B,4)=0
- 类
A
A
A
- 簇5 {p4,p5}
- 类
A
A
A
R ( A , 5 ) = 0 R(A,5) = 0 R(A,5)=0
P ( A , 5 ) = 0 P(A,5) = 0 P(A,5)=0
F ( A , 5 ) = 0 F(A,5) = 0 F(A,5)=0 - 类
B
B
B
R ( B , 5 ) = 2 5 R(B,5) = \frac{2}{5} R(B,5)=52
P ( B , 5 ) = 2 2 P(B,5) = \frac{2}{2} P(B,5)=22
F ( B , 5 ) = 0.57 F(B,5) =0.57 F(B,5)=0.57
- 类
A
A
A
- 簇6 {p3,p6}
- 类
A
A
A
R ( A , 6 ) = 1 3 R(A,6) = \frac{1}{3} R(A,6)=31
P ( A , 6 ) = 1 2 P(A,6) = \frac{1}{2} P(A,6)=21
F ( A , 6 ) = 0.4 F(A,6) = 0.4 F(A,6)=0.4 - 类
B
B
B
R ( B , 6 ) = 1 5 R(B,6) = \frac{1}{5} R(B,6)=51
P ( B , 6 ) = 1 2 P(B,6) = \frac{1}{2} P(B,6)=21
F ( B , 6 ) = 0.29 F(B,6) =0.29 F(B,6)=0.29
- 类
A
A
A
- 簇7 {p7,p8}
- 类
A
A
A
R ( A , 7 ) = 0 R(A,7) = 0 R(A,7)=0
P ( A , 7 ) = 0 P(A,7) = 0 P(A,7)=0
F ( A , 7 ) = 0 F(A,7) = 0 F(A,7)=0 - 类
B
B
B
R ( B , 7 ) = 2 5 R(B,7) = \frac{2}{5} R(B,7)=52
P ( B , 7 ) = 2 2 P(B,7) = \frac{2}{2} P(B,7)=22
F ( B , 7 ) = 0.57 F(B,7) =0.57 F(B,7)=0.57
- 类
A
A
A
所以,
对类
A
A
A:
F
(
A
)
=
m
a
x
F
(
A
,
i
)
=
0.8
F(A) = max{F(A,i)} = 0.8
F(A)=maxF(A,i)=0.8
对类
B
B
B:
F
(
B
)
=
m
a
x
F
(
B
,
i
)
=
0.77
F(B) = max{F(B,i)} = 0.77
F(B)=maxF(B,i)=0.77
F = 3 8 × F ( A ) + 5 8 × F ( B ) = 0.78 F = \frac{3}{8} × F(A) + \frac{5}{8} ×F(B) = 0.78 F=83×F(A)+85×F(B)=0.78
8
1
→
D
1\rightarrow D
1→D
2
→
C
2\rightarrow C
2→C
3
→
A
3\rightarrow A
3→A
4
→
B
4\rightarrow B
4→B
9
SNN相似度:
| 点 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 2 | 0 | 0 | 1 |
| 2 | 0 | 2 | 1 | 0 |
| 3 | 0 | 1 | 2 | 0 |
| 4 | 1 | 0 | 0 | 2 |












![[论文阅读笔记31]Mamba (Selective Structured State Space Model) 及其应用](https://img-blog.csdnimg.cn/direct/b270c0fb2e0148e09188c58e74ebc44a.png)