（一）等价表的整理与压缩
1.1 等价关系的识别与追踪
在初步标记过程完成后，等价表的整理和压缩变得至关重要。这一阶段的首要任务是从等价表的地址1开始，对等价表进行逐个扫描。在扫描过程中，系统将检查每个临时标记是否存在等价关系。若发现等价关系，系统将执行追踪过程，以确保具有等价关系的标记能够被最小化，并在等价表中进行相应的更新。

1.2 等价表的压缩过程
等价表压缩的目的是简化标记，以便于后续处理。这一过程从自然数1开始，对等价表中的每个标记进行重新赋值。具体操作如下：首先设置两个指针k和j，其中k为当前检查的标记，j为压缩后的最终标记。若E(k)等于k本身，则将E(k)更新为j并递增j的值。否则，执行递归操作E(k) = E(E(k))，直到找到最小的等价标记，然后更新E(k)为该最小标记。这一过程确保了所有具有连通关系的标记都指向了它们的最终标记。

1.3 等价表操作的可视化
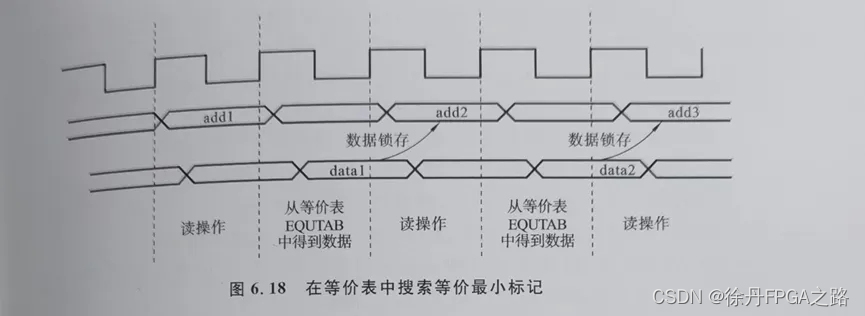
为了更好地理解等价表的搜索和操作过程，图6.18提供了一个可视化的示例。该图展示了在不同地址下进行读操作时，如何从等价表EQUTAB中获取数据，并展示了如何通过读周期发送读写控制信号来获取最小等价标记。如果获取到的数据与地址相等，则表明当前标记即为最小标记。

1.4 搜索和操作的三种情况
在整理等价表时，每个临时标记的搜索和操作可以归纳为三种情况：

若E(l)等于l，则无需进行任何处理。

若E(l)等于a，且E(a)也等于a，则同样无需处理。

若E(l)等于t1