目录

二叉树的概念： 

二叉树的应用与实现： 

 二叉树实现接口：

通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树 

 二叉树节点个数​编辑

二叉树叶子节点个数 

二叉树第k层节点个数 

 二叉树查找值为x的节点​编辑

 二叉树前序遍历，中序遍历，后序遍历

层序遍历 

判断二叉树是否是完全二叉树 

二叉树销毁 

---

二叉树的概念： 

        在前面的学习中我们认识了树的概念，今天的我们将学习数中比较特殊的一类：二叉树。

二叉树故名思意，这种树只存在两个分支，图形相貌如下： 

 而二叉树中又存在着特殊的两类：满二叉树和完全二叉树。

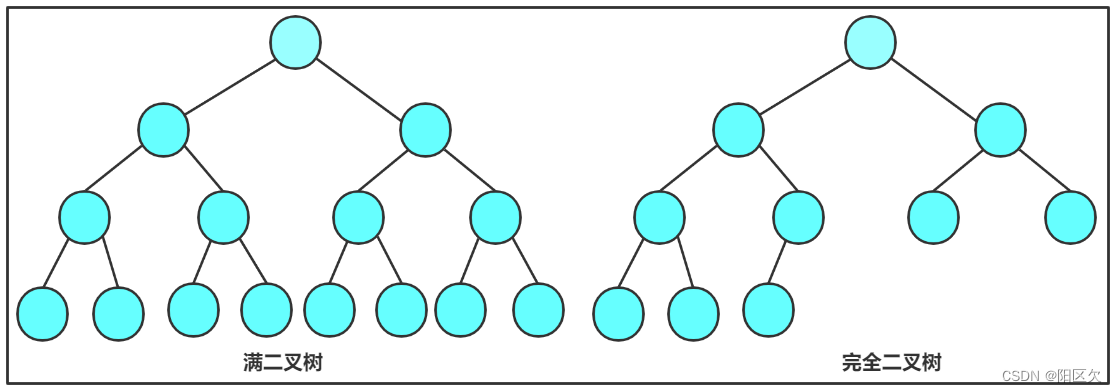
• 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是 ，则它就是满二叉树。
  
   
•  完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

二叉树的性质
1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 2^(i-1)个结点。
2. 若规定根结点的层数为1，则深度为h的二叉树的最大结点数是 2^h-1。
3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2,则有n0＝ n2＋1。4. 若规定根结点的层数为1，具有n个结点的满二叉树的深度，h=log(n+1) (ps： 是log以2
为底，n+1为对数)
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有结点从0开始编号，则对于序号为i的结点有：
1. 若i>0，i位置结点的双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
2. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
3. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

二叉树的应用与实现： 

 二叉树实现接口：

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>


// 类型的定义
typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

// 函数的声明

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);

// 二叉树销毁
void BinaryTreeDestory(BTNode* root);

// 二叉树节点个数
int BinaryTreeSize(BTNode* root);

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);

通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树 

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	if (a[(*pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("malloc fail!");
		return 1;
	}

	root->_data = a[(*pi)++];
	root->_left = BinaryTreeCreate(a, pi);
	root->_right = BinaryTreeCreate(a, pi);

	return root;
}

 二叉树节点个数

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

二叉树叶子节点个数 

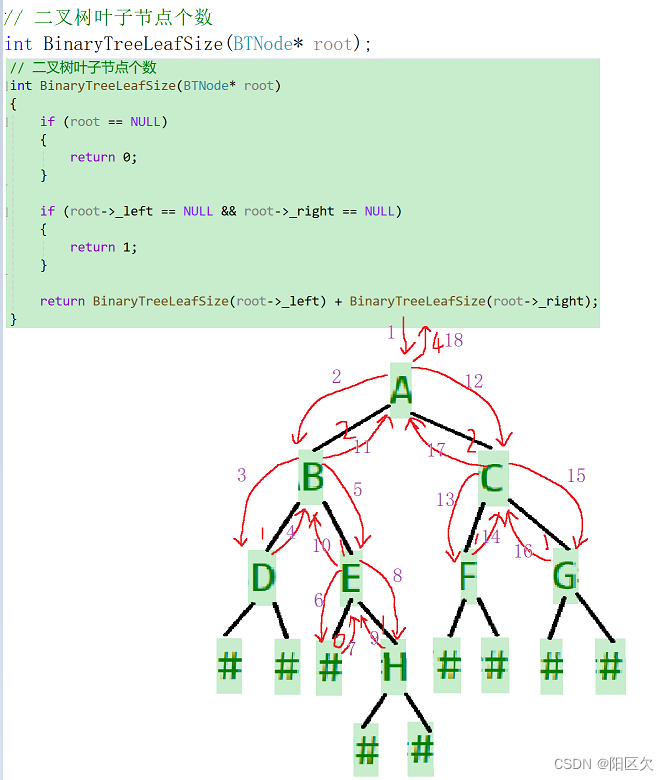
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->_left == NULL && root->_right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

二叉树第k层节点个数 

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->_left, k - 1) +
		   BinaryTreeLevelKSize(root->_right, k - 1);
}

 二叉树查找值为x的节点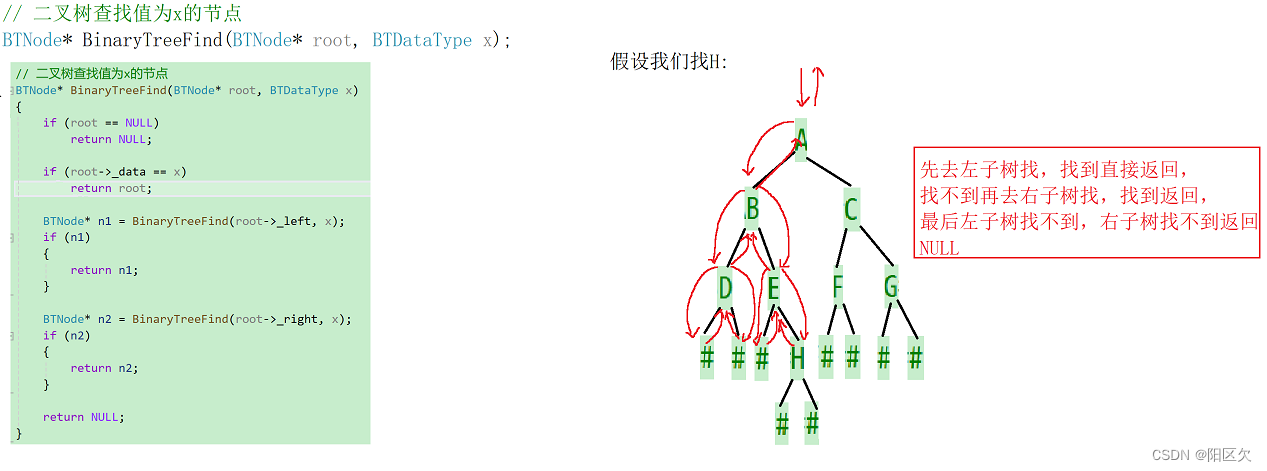

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->_data == x)
		return root;

	BTNode* n1 = BinaryTreeFind(root->_left, x);
	if (n1)
	{
		return n1;
	}

	BTNode* n2 = BinaryTreeFind(root->_right, x);
	if (n2)
	{
		return n2;
	}

	return NULL;
}

 二叉树前序遍历，中序遍历，后序遍历

 

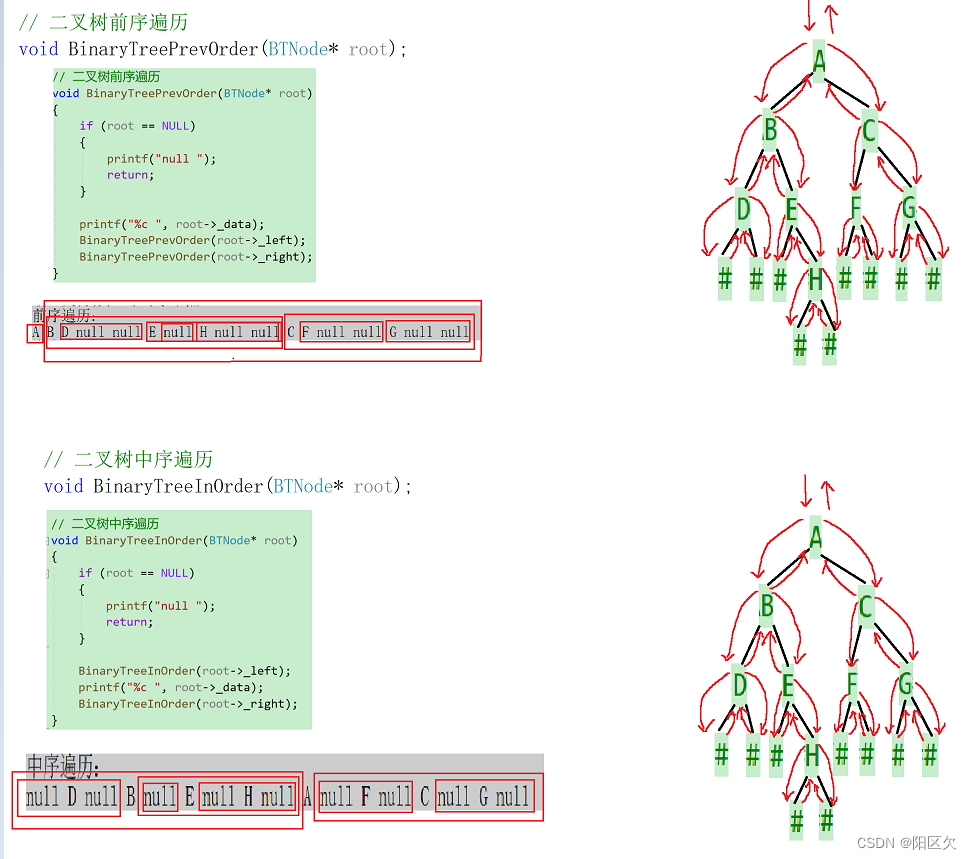
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("null ");
		return;
	}

	printf("%c ", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("null ");
		return;
	}

	BinaryTreeInOrder(root->_left);
	printf("%c ", root->_data);
	BinaryTreeInOrder(root->_right);
}

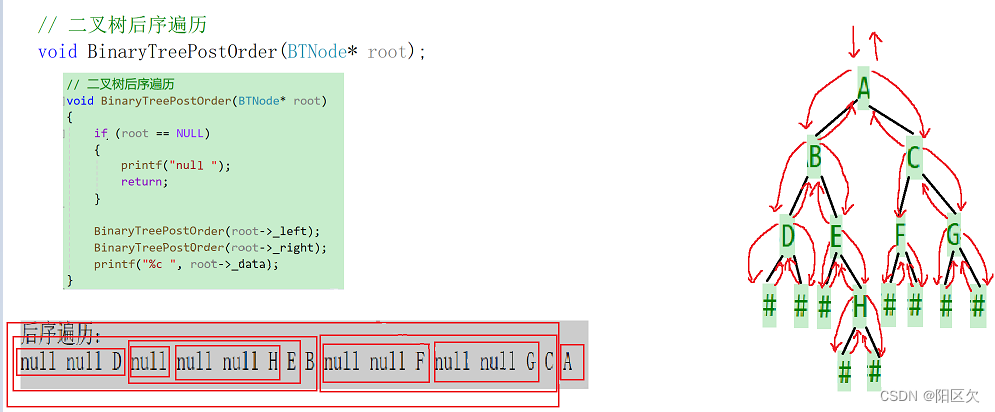
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("null ");
		return;
	}

	BinaryTreePostOrder(root->_left);
	BinaryTreePostOrder(root->_right);
	printf("%c ", root->_data);
}

层序遍历 

void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		printf("%c ", front->_data);

		if (front->_left)
			QueuePush(&q, front->_left);

		if (front->_right)
			QueuePush(&q, front->_right);
	}

	QueueDestroy(&q);
}

判断二叉树是否是完全二叉树 

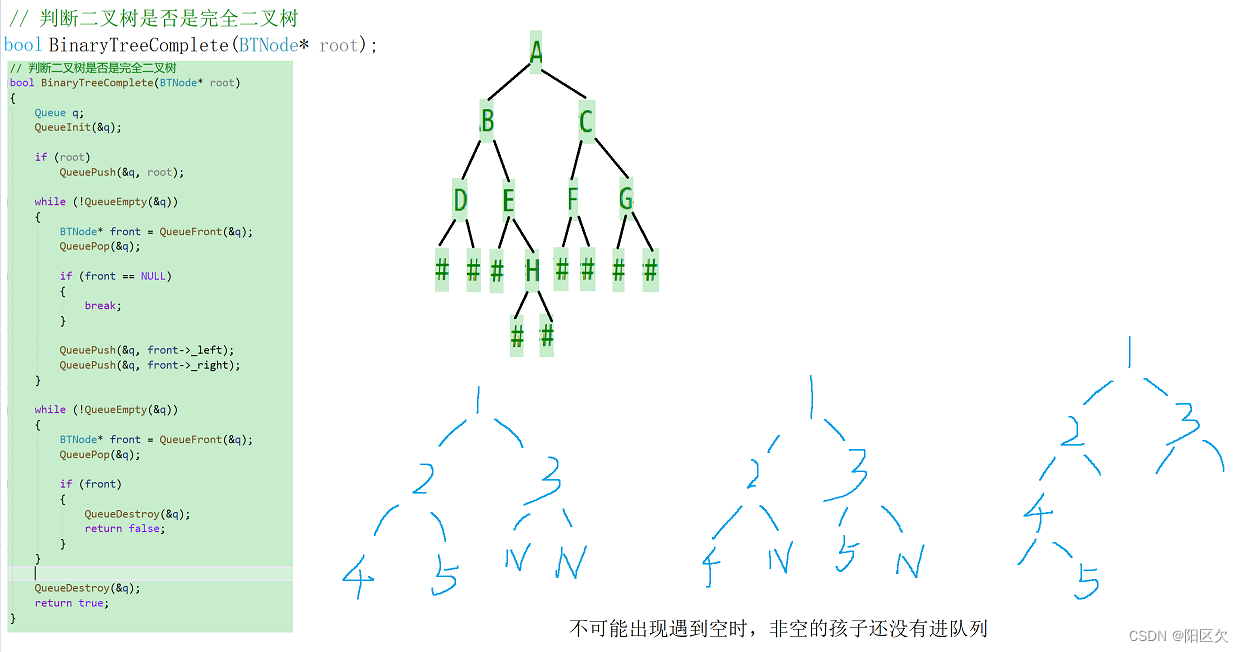
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front == NULL)
		{
			break;
		}

		QueuePush(&q, front->_left);
		QueuePush(&q, front->_right);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;
}

二叉树销毁 

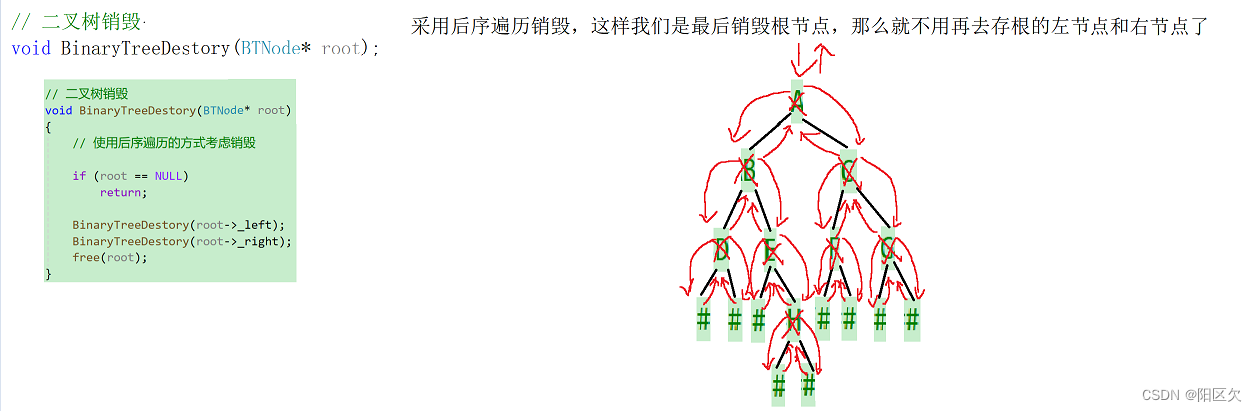
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	// 使用后序遍历的方式考虑销毁

	if (root == NULL)
		return;

	BinaryTreeDestory(root->_left);
	BinaryTreeDestory(root->_right);
	free(root);
}

 代码完整文件：BinaryTree_implement_by_C_2024_5_27 · 阳区欠/数据结构的学习 - 码云 - 开源中国 (gitee.com)