十大排序 —— 冒泡排序
- 什么是冒泡排序
- 基本步骤
- 特点
- 优化
- 冒泡的各项性能
- 时间复杂度
- 空间复杂度
- 稳定性
- 总结
我们今天来讲一个大家熟悉的老朋友——冒泡排序:
什么是冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法,因其工作原理像水底下的气泡逐渐上升至水面而得名。它重复地遍历要排序的数列,比较每对相邻元素的值,如果它们的顺序错误(例如在升序排序中前者大于后者),就交换它们的位置。遍历过程会重复进行,直到整个数列变成有序状态,也就是说在某一次遍历中没有发生任何交换,这表明数列已经是有序的。
基本步骤
- 比较相邻元素:从数列的第一个元素开始,对每一对相邻元素做比较。
- 交换位置:如果第一个元素大于第二个元素(升序排序的情况下),就交换它们的位置。否则,不做交换,继续比较下一对元素。
- 重复上述过程:每次遍历都将未排序部分的最大值(升序时)移至末尾。
- 终止条件:当整个数列遍历完一遍后,如果没有发生过交换,说明数列已经是有序的,排序结束。
特点
- 稳定性:冒泡排序是稳定的排序算法,即相等的元素在排序前后相对位置不会改变。
- 时间复杂度:最好情况下(输入数组已经是排序好的)为O(n),但最坏和平均情况下的时间复杂度均为O(n^2),其中n是数列的长度。
- 空间复杂度:O(1),因为排序是原地进行的,不需要额外的存储空间。
- 效率:由于其较高的时间复杂度,冒泡排序在大规模数据集上效率较低,通常用于教学目的或小规模数据排序。
举个例子
#include <iostream>
// 冒泡排序函数
// 参数: a - 指向待排序数组的指针, size - 数组的大小
void Bubble_Sort(int *a, int size) {
// 外层循环控制遍历的轮数,每轮将剩余未排序部分的最大元素放到末尾
for(int i = 0; i < size; i++) {
// 内层循环负责每一轮的具体比较和交换操作
// 注意:由于每轮外循环后,最大的元素已经被排到了末尾,所以下一轮可以减少一次比较
for(int j = 0; j < size - i - 1; j++) {
// 如果当前元素大于下一个元素(这里应是降序排序,若需升序则应改为a[j] > a[j + 1])
if(a[j] < a[j + 1]) {
// 交换元素位置
int temp = a[j+1]; // 临时保存较大值
a[j+1] = a[j]; // 将较小值移到后面
a[j] = temp; // 将较大值移到前面
}
}
}
}
// 打印数组函数
// 参数: a - 指向数组的指针, size - 数组的大小
void Print(int *a, int size) {
// 遍历数组并打印每个元素
for(int i = 0; i < size; i++) {
std::cout << a[i] << " ";
}
// 每行打印结束后换行
std::cout << std::endl;
}
// 程序主入口
int main() {
// 定义并初始化一个整型数组
int arr[] = {64, 34, 25, 12, 22, 11, 90};
// 计算数组的元素数量
int n = sizeof(arr)/sizeof(arr[0]);
// 打印原始数组
Print(arr, n);
// 调用冒泡排序函数对数组进行排序
Bubble_Sort(arr, n);
// 打印排序后的数组
Print(arr, n);
return 0; // 程序正常结束
}

我们画个图:
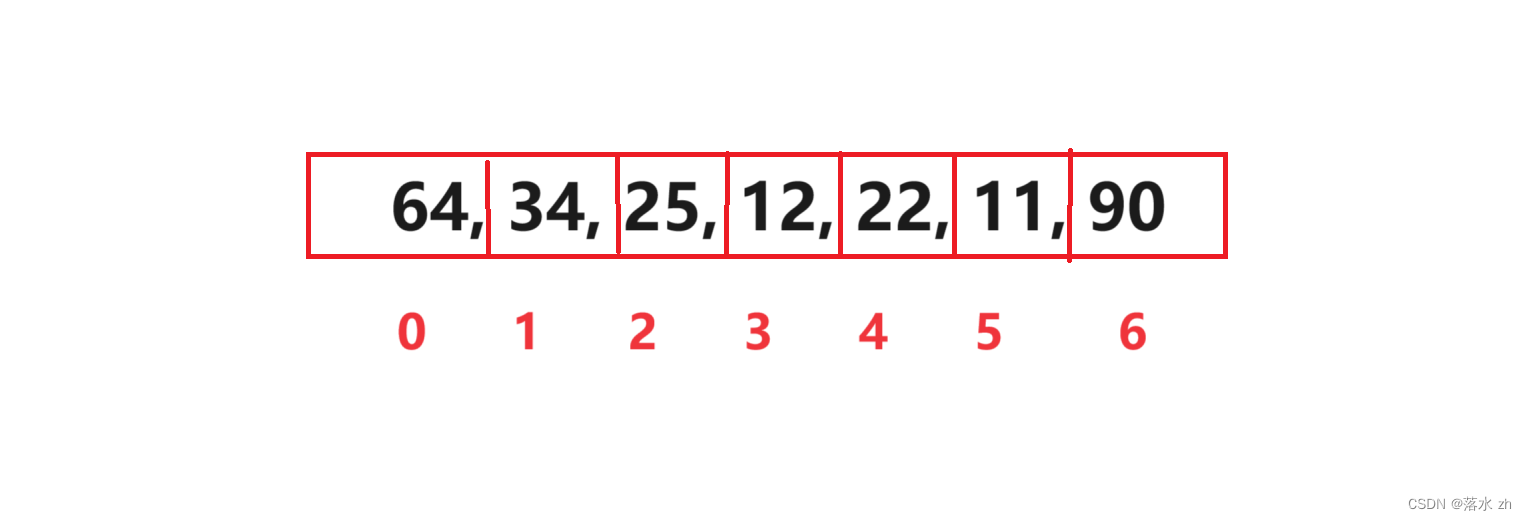
当 i = 0时,就是64和面的数字比较:
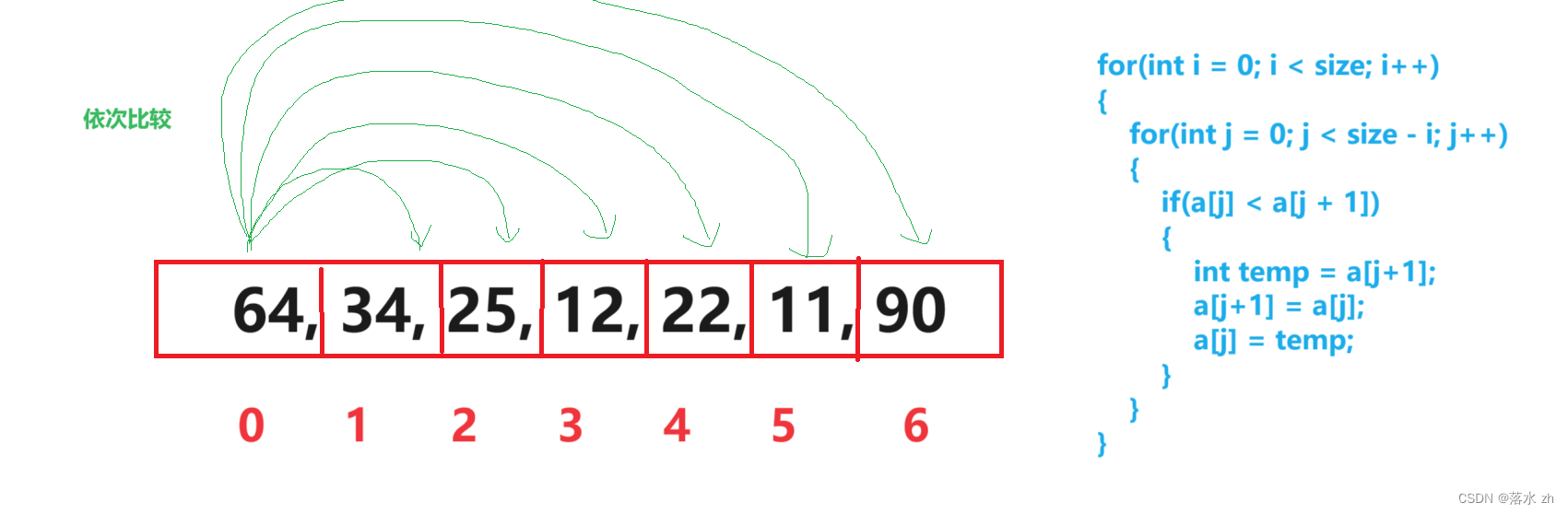
发现90比自己大,64和90交换:

此时下标j到了6,一轮结束的标志就是 j + 1 < size:
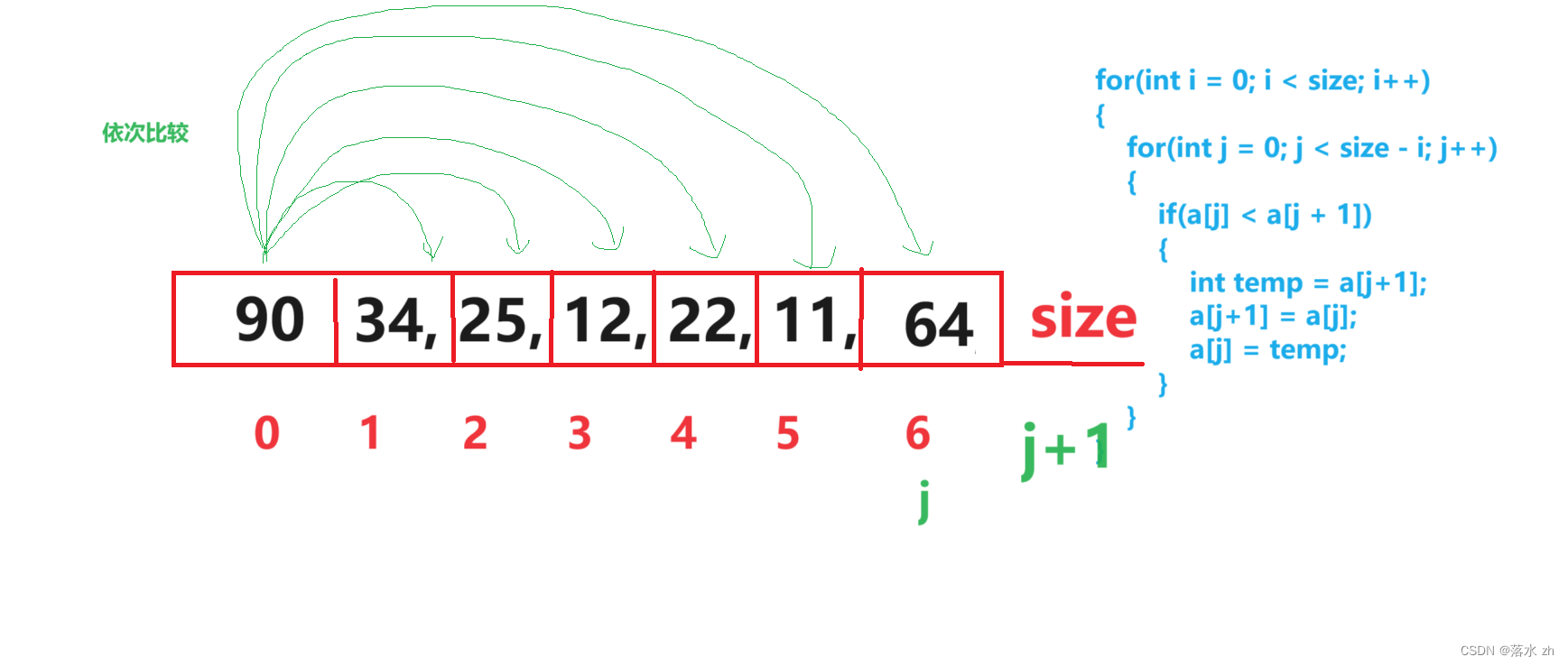
此时开始第二轮,因为我们第一个数比较过了,我们可以从34之后的数开始,比较5个数,之后再来一轮,比较4个数…这就是内循环的写法的原因:
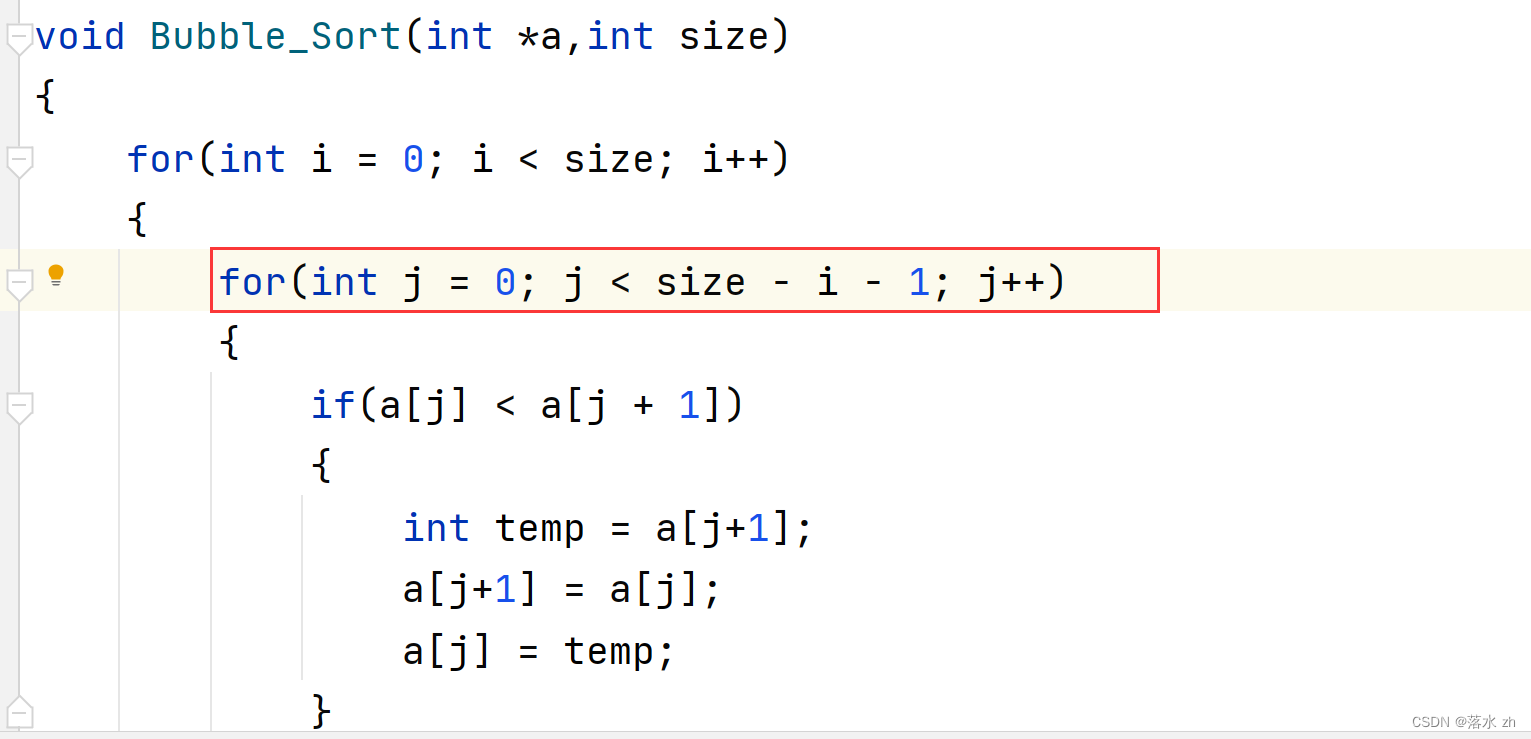
优化
- 提前终止:设置一个标志位,用于记录在一次完整的遍历中是否发生了交换,如果没有交换,说明数组已经是有序的,可提前结束排序。
- 记录最后一次交换的位置:下次遍历只需到该位置,因为之后的元素已经是有序的。
我们这里用提前终止:
#include <iostream>
// 冒泡排序函数,包含提前终止的优化
// 参数: a - 指向待排序数组的指针, size - 数组的大小
void Bubble_Sort(int *a, int size) {
// 外层循环控制遍历的轮数
for(int i = 0; i < size; i++) {
bool swapped = false; // 添加一个标记,用于检查本轮循环中是否有交换发生
// 内层循环负责具体比较和交换操作
// 注意:每轮外循环后,最大的元素已经被排到了末尾,所以下一轮可以减少一次比较
for(int j = 0; j < size - i - 1; j++) {
// 检查当前元素是否小于下一个元素(这里实现的是降序排序,升序应为a[j] > a[j + 1])
if(a[j] < a[j + 1]) {
// 交换元素
int temp = a[j+1]; // 临时保存较大值
a[j+1] = a[j]; // 将较小值移到后面
a[j] = temp; // 将较大值移到前面
swapped = true; // 标记有交换发生
}
}
// 如果在某次遍历中没有发生任何交换,说明数组已经是有序的,可以提前结束排序
if(!swapped) break;
}
}
// 打印数组的函数
// 参数: a - 指向数组的指针, size - 数组的元素数量
void Print(int *a, int size) {
// 遍历数组并打印每个元素
for(int i = 0; i < size; i++) {
std::cout << a[i] << " ";
}
// 每行打印完毕后换行
std::cout << std::endl;
}
// 主函数
int main() {
// 初始化一个整型数组
int arr[] = {64, 34, 25, 12, 22, 11, 90};
// 计算数组长度
int n = sizeof(arr)/sizeof(arr[0]);
// 打印原始数组
Print(arr, n);
// 对数组进行冒泡排序
Bubble_Sort(arr, n);
// 打印排序后的数组
Print(arr, n);
return 0; // 程序正常退出
}
冒泡的各项性能
冒泡排序(Bubble Sort)作为一种基础的排序算法,其主要性能指标包括时间复杂度、空间复杂度和稳定性。下面是这些性能指标的详细解释:
时间复杂度
- 最好情况(最优时间复杂度):当输入数组已经是排序好的情况下,冒泡排序只需进行一轮遍历就可以判断出数组已经有序,此时的时间复杂度为 O(n),其中n是数组的长度。
- 最坏情况(最劣时间复杂度):当输入数组是逆序的,即每个元素都位于其正确位置的对面,冒泡排序需要进行n-1轮遍历,每轮遍历中都需要进行n-i次比较(因为每轮都会把一个元素放到最终位置,所以比较次数递减),总比较次数接近n(n-1)/2,因此最坏情况下的时间复杂度为 O(n^2)。
- 平均时间复杂度:考虑到各种随机排列的可能性,冒泡排序的平均时间复杂度也是 O(n^2)。
空间复杂度
冒泡排序是一种原地排序算法,它不需要额外的存储空间来存放数据,除了几个用于交换的临时变量。因此,它的空间复杂度为 O(1)。
稳定性
冒泡排序是稳定的排序算法。这意味着相等的元素在排序前后相对位置不会改变。这是因为冒泡排序在交换元素时只会交换不满足排序条件的相邻元素,如果元素相等则不会进行交换,从而保持了稳定性。
总结
尽管冒泡排序由于其简单易懂而常用于教学,但由于其较高的时间复杂度,在处理大量数据时效率低下,通常不推荐在实际应用中使用,特别是在数据量大的场景下。在需要高效排序的场合,更高效的算法如快速排序、归并排序或堆排序等是更好的选择。然而,冒泡排序在小规模数据或者几乎已排序的数据集上可能表现得还可以接受,特别是经过优化(如添加提前终止的条件)后。