1.铺垫概念

⭐有向无环图（DAG图）

有向无环图是一种特殊的图数据结构。在这样的图中，节点之间通过有向边连接，表示从一个节点到另一个节点的单向关系，并且不存在任何形式的环路，即没有路径可以让你从一个节点出发，沿着一系列有向边最终又回到该节点。

• 有向性：图中的每条边都有方向，可以用箭头表示，指示从起点到终点的单向关系。
• 无环性：是说在图中找不到一个起点到终点的路径，其中起点和终点为同一个点，或者通过一系列边能够形成一个环状结构。这意味着从任意节点出发，沿着边走，你永远不会回到起点或之前访问过的节点。
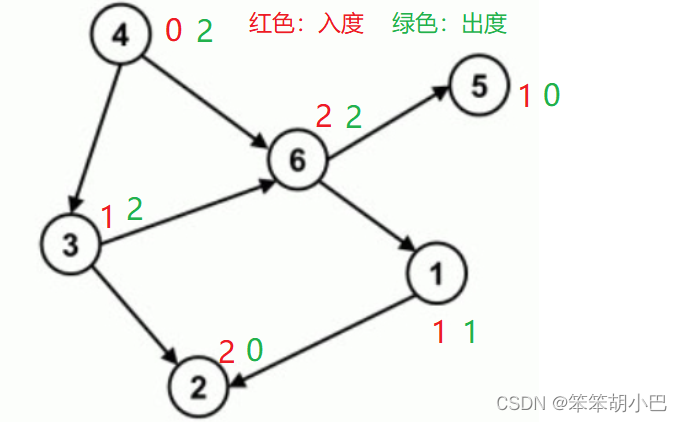
• 入度：指有多少条有向边指向该节点。
• 出度：指从该节点出发的有向边的数。

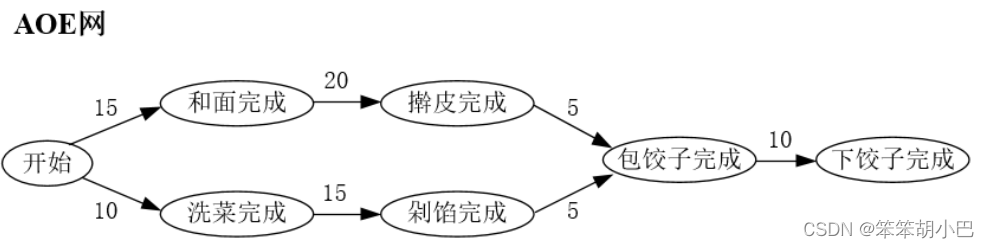
⭐AOV网 - 顶点活动图

AOV网就是在有向无环图中每一个顶点代表一个活动，而有向边则表示活动之间的优先关系的图结构。

⭐拓扑排序

拓扑排序是对一个有向无环图的顶点进行排序的一种方法，找到做事情的先后顺序，拓扑排序的结果可能不唯一。

进行拓扑排序的步骤通常如下：

1. 选择起点：选择一个入度为0的顶点并输出。
2. 删除起点及关联边：从图中删除该顶点及其所有出度边。
3. 重复上述两步，直到当前图中没有节点为止(无环)或者没有入度为0的点为止(有环)。如果在这个过程中能访问到所有节点，说明原图是一个有向无环图，且存在至少一种拓扑排序；反之，如果还有节点未被访问到，则说明原图中存在环，无法进行拓扑排序。

应用：判断图中是否有环。

⭐拓扑排序的实现

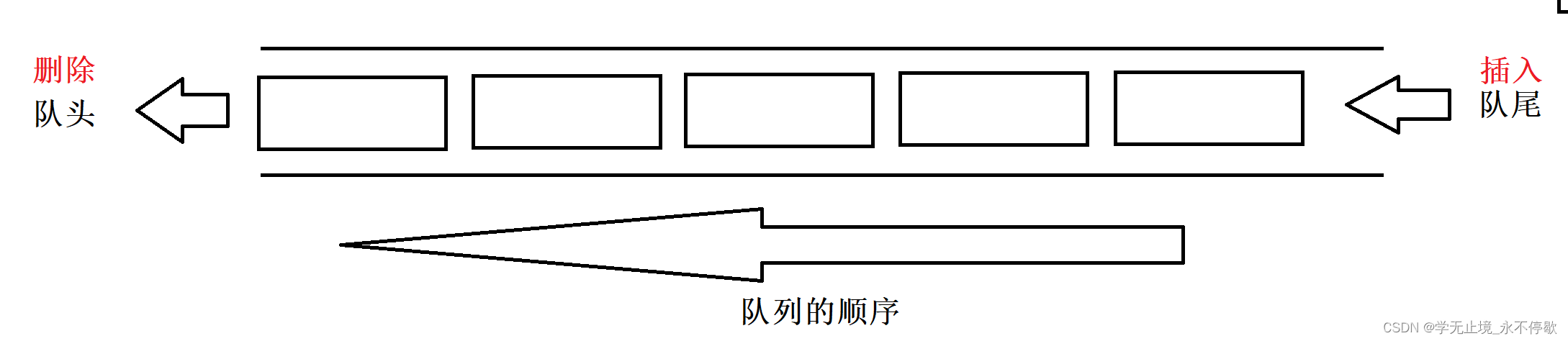
借助队列，进行一次bfs即可

1.初始化：把所有入度为0的点加入到队列

2.当队列不为空的时候

• 拿出队头元素，加入到最终结果中
• 删除与该元素相连的边
• 判断与删除边相连的点的入度是否为0，如果入队为0，加入到队列中

2.课程表

这个题目给的实例比较简单，我们重新来给一个案例来快速了解这个题目。

所以解决我们就要先构建图代码中展示，随后进行拓扑排序即可，直接来看拓扑排序的思路：

直接上代码：

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        // 1.把所有的节点存储到一个图结构中
        unordered_map<int, vector<int>> edges;// 邻接表存图
        vector<int> in(numCourses); // 统计每一个节点的入度
        // 2.建图
        for(auto& e : prerequisites)
        {
            int a = e[0];
            int b = e[1];
            // b -> a 的一条边
            edges[b].push_back(a);
            in[a]++;
        }
        // 3.拓扑排序
        // (1)把所有入度位0的节点加入到队列中
        queue<int> q;
        for(int i = 0; i < in.size(); i++)
            if(in[i] == 0) // 入度为0
                q.push(i); // i是节点
        // bfs
        while(q.size())
        {
            int t = q.front();
            q.pop();
            // (2)删除与该元素相连的边 
            for(auto e : edges[t])
            {
                in[e]--; // 入度--
                // (3)如果入度为0,加入到队列中
                if(in[e] == 0)
                    q.push(e);
            }   
        }
        // 判断是否有环
        for(int i = 0; i < in.size(); i++)
            if(in[i] != 0)
                return false;
        return true;
    }
};

3.课程表II

这个题目和上一个题目基本上差不多，唯一就多了一个要求就是求解拓扑排序的序列，我们在bfs中利用一个vector存一下每次取出的队头元素即可，直接上代码：

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> edges(numCourses); //邻接表存图
        vector<int> in(numCourses); // 统计入度

        // 1.建图
        for(auto& e : prerequisites)
        {
            int a = e[0];
            int b = e[1];
            // 关系:b -> a 
            edges[b].push_back(a);
            // 统计入度
            in[a]++;
        }

        // 2.拓扑排序
        queue<int> q;
        for(int i = 0; i < numCourses; i++)
            if(in[i] == 0)
                q.push(i);

        // 3.bfs
        vector<int> ret; //存储拓扑排序结果
        while(q.size())
        {
            int t = q.front();
            q.pop();
            ret.push_back(t);
            for(auto e : edges[t])
            {
                // 删除所有与该元素相连的边
                in[e]--;
                if(in[e] == 0) 
                    q.push(e);
            }
        }

        // 4.判断是否有环
        if(ret.size() == numCourses)
            return ret;
        return {};
    }
};

4.火星词典

将题意搞清楚之后，这道题就变成了判断有向图时候有环，可以⽤拓扑排序解决，直接上思路：

直接上代码：

class Solution {
    unordered_map<char, unordered_set<char>> edges; // 邻接表建图
    unordered_map<char, int> in; // 统计入度
    bool check; // 处理边界情况
public:
    string alienOrder(vector<string>& words) {
        // 1.建图 + 初始化入度哈希表
        for(auto& s : words)
        {
            for(auto ch : s)
            {
                in[ch] = 0;
            }
        }
        for(int i = 0; i < words.size(); i++)
        {
            for(int j = i + 1; j < words.size(); j++)
            {
                // 添加到add数组
                add(words[i], words[j]);
                // 边界情况
                if(check) return "";
            }
        }
        
        // 2.拓扑排序
        queue<char> q;
        for(auto [a, b] : in)
            if(b == 0) 
                q.push(a);
        // 3.bfs
        string ret; // 统计结果
        while(q.size())
        {
            char t = q.front();
            q.pop();
            ret += t;
            for(auto e : edges[t])
            {
                in[e]--;
                if(in[e] == 0)
                    q.push(e);
            }
        }

        // 判断是否有环
        for(auto& [a, b] : in)
            if(b != 0) return "";
        
        return ret;
    }

    void add(string& s1, string& s2)
    {
        int n = min(s1.size(), s2.size());
        int i = 0;
        for( ; i < n; i++)
        {
            if(s1[i] != s2[i])
            {
                char a = s1[i], b = s2[i]; // a -> b
                if(!edges.count(a) || !edges[a].count(b))
                {
                    edges[a].insert(b);  
                    in[b]++;
                }
                break;
            }
        }
        if(i == s2.size() && i < s1.size()) check = true;
    }
};