在物理世界中，数百个这样的极限或界限已被发现和证实。它们合在一起，构成了现实的一道屏障。马尔可夫不等式和比奈梅-切比雪夫不等式就是这样的两个界限，它们深刻地影响了我们对自然界对随机事件发生频率的限制的认识。

        马尔可夫不等式的发现和证明归功于才华横溢、充满激情的原则性的俄罗斯数学家安德烈·安德烈耶维奇·马尔可夫 (1856-1922)。

AA马尔可夫（CC0）

        Bienaymé-Chebyshev 不等式的发明者应归功于两个人：概率论巨擘、马尔可夫的老师 — — 令人敬畏的帕夫努蒂·利沃维奇·切比雪夫 (1821-1894)，以及切比雪夫的法国同事兼朋友 Irénée-Jules Bienaymé (1796-1878)。

Bienaymé（左）和Chebyshev（CC0）

        这些不等式的发现有着如此非凡的历史——尤其是比耶奈梅-切比雪夫不等式——以至于如果不涉及产生这些不等式的人物和故事，那么简单地抛出数学结论是远远不够的。我将尝试揭示这些背景故事。这样做，我将为解释这些不等式背后的数学原理奠定基础。

        我先从马尔可夫不等式开始，然后展示 Bienaymé–Chebyshev 不等式是如何通过对马尔可夫不等式进行一些简单的变量替换而产生的。为了增加乐趣，我们将获得我们的大奖——弱大数定律(WLLN) 的证明——展示 WLLN 是如何几乎毫不费力地从对 Bienaymé–Chebyshev 不等式进行另一组变量替换而产生的。

三、马尔可夫不等式

马尔可夫这个名字让人想起“马尔可夫链”、“马尔可夫过程”和“马尔可夫模型”。严格来说，马尔可夫链是 AA 马尔可夫创造的。但马尔可夫对数学的贡献远远超出了马尔可夫链和概率论。马尔可夫是一位多产的研究人员，发表了 120 多篇论文，涵盖了数论、连续分数、微积分和统计学等广泛的思想。顺便说一句，马尔可夫主要在俄语期刊上发表文章，而他的博士导师 PL 切比雪夫则在西欧，尤其是法国的出版物上发表了大量文章。

3.1 最早提出

1900 年，马尔可夫很可能正处于职业生涯的巅峰时期，他出版了一本关于概率的开创性著作，名为《概率微积分》。

马尔可夫著作《概率计算》的 1900 年版 (互联网档案馆。CC0 )

这本书出版了 4 个版本和德语版本。马尔可夫在 1913 年特意出版了这本书的第 3 版，以纪念弱大数定律 (WLLN) 200 周年。第 3 版中有大量材料专门用于 WLLN。但在一个引理中隐藏着马尔可夫对一个定律的证明，这个定律对统计科学领域至关重要，以至于它经常被用作 WLLN 本身证明的起点。

马尔可夫不等式基于五个相关概念：

1. 随机变量X
2. X的概率分布
3. 在X的域中选择的任意参考值“a”
4. X的平均值
5. 观测值X

马尔可夫不等式将这五个简单的概念联系在一起形成了一个定理。马尔可夫证明了以下内容：

想象任何一个非负随机变量X。X可以表示一些平凡的事情，比如你早上起床的时间。也可以表示一些巨大的东西，比如一个星系中的星星数量。X可以是离散的，也可以是连续的。X可以具有任何类型的概率分布。简而言之，X可以表示任何非负随机现象。现在在X的范围内选择一个值 — — 任意值。我们将这个值表示为“a”。马尔可夫表明，大自然对观察到大于或等于你选择的值“a”的 X 值的概率施加了一个上限。并且这个上限会随着“a”的增加而缩小。你选择的值“a”越大，观察到另一个超过“a”的值“b”的概率就越低。换句话说，大自然厌恶异常值。

为了说明这一点，请看下面的图表。它显示了美国最富裕的 20 个州的县人均个人收入的频率分布。

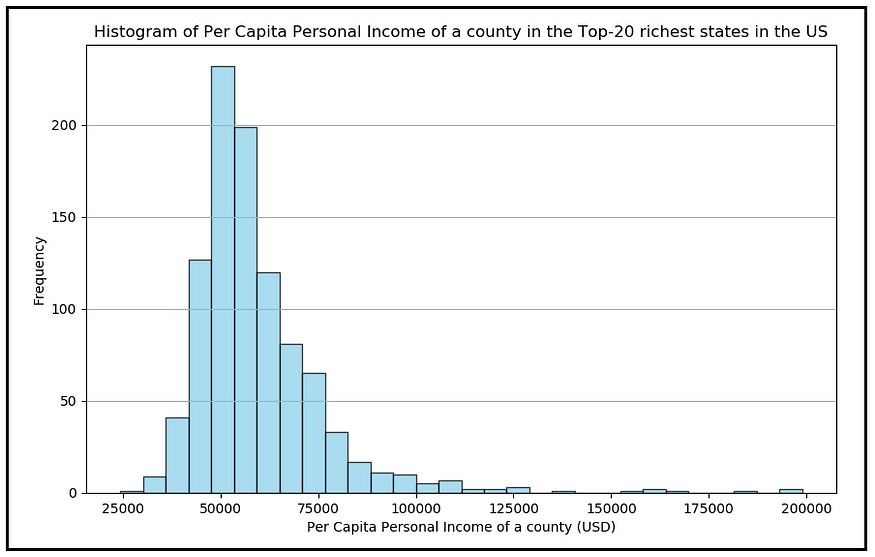
美国最富裕的 20 个州各县人均个人收入直方图（图片来自作者）（数据来源：美国经济分析局通过版权政策）

这里，随机变量X是随机选择的县的人均收入。

现在让我们用某个阈值“a”来计算人均收入。在下面的图像面板中，红色区域表示X ≥ a，其中 a = 50000 美元、70000 美元和 80000 美元。

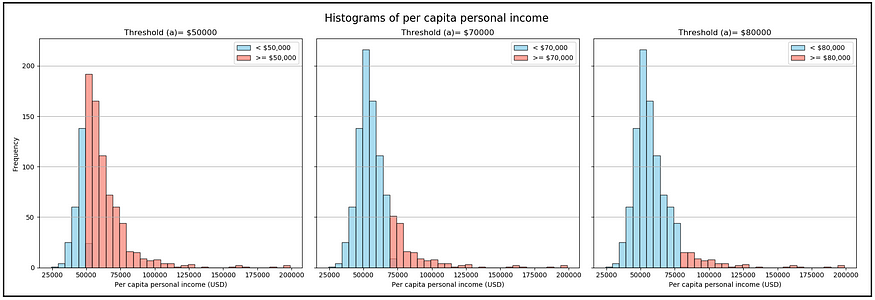
随着 'a' 的增加，P( X≥a ) 减小（作者图片）

概率 P( X ≥ a) 是红色区域面积与直方图下总面积的比率。很容易看出，这个概率 P( X ≥ a) 随着“a”的增加而减小。它与“a”成反比。马尔可夫定理对这个概率施加了一个特定的上限，它与“a”的值成反比。无论X的分布如何，这种关系都成立。

但这并不是马尔可夫所展示的全部。

作为同一不等式的一部分，马尔可夫还表明X 的平均值直接影响观察到 X >= a 的概率。 X的平均值越大，该概率的上限越高，反之亦然。换句话说，随着X的概率质量向X范围的上限移动，P( X >= a)的上限也会增加。相反，如果X的概率质量向下端移动，使其“底部沉重”，则观察到较大X值的概率会降低。

其中一些听起来像是日常常识，但马尔可夫的聪明之处在于建立了“a”（P（X >=a））和X的平均值（又称期望值）之间的数学精确关系，表示为 E（X）。他证明了：

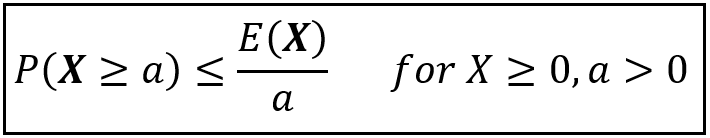
马尔可夫不等式（作者提供图片）

3.2 马尔可夫不等式的证明

        有很多方法可以证明马尔可夫不等式。我将介绍一种简单的方法，无论X是离散的还是连续的，该方法都有效。X只需为非负数即可。

        和以前一样，我们使用您感兴趣的一些阈值“a”。

        现在我们定义一个随机变量I，当 0 ≤ X < a时， I = 0；当X ≥ a 时， I = 1。在统计学术语中，I称为指示变量。

考虑X ≥ a的情况。将两边乘以I：

XI≥aI​​

当X≥a时，I =1，所以XI = X。

因此，

当I = 1 时， X ≥ a I（让我们记住这个结果）。

由于 X 为非负数，0 ≤ X，并且对于某个正数“a”，X 可以小于“a”，也可以大于或等于“a”。我们已经考虑过X大于或等于 a 的情况。因此，让我们考虑 0 ≤ X < a的情况。

根据I的定义，当X < a 时，I = 0。

因此，a I = a0 = 0

由于X被假定为非负数，即X > 0 且 a I = 0，因此X ≥ a I

因此，无论I = 1 还是I = 0，I <= X。

让我们在这个不等式的两边应用期望算子 E(.)：

E(a I ) <= E( X )

取出常数 'a'：

aE(I) <= E( X )

        让我们来研究一下 E( I )。随机变量I只能取两个值：0 和 1，分别对应 X < a 和 X≥ a。与每个事件相关的概率分别为 P( X < a) 和 P( X >= a)。因此，

        E（I）= 0P（X <a）+ 1P（X >=a）= P（X >=a）

将此结果代入 aE( I ) <= E( X ) 中，我们得到：

        aP( X >= a) <= E( X )

因此：

        P( X >=a)<=E( X )/a，这是马尔可夫证明的不等式。

四、 Bienaymé–Chebyshev 不等式

        Bienaymé-Chebyshev 不等式指出，在距离随机变量平均值“a”个单位处观察到值的概率与马尔可夫不等式类似。换句话说，自然对概率 P(| X — E( X )| >= a) 施加了一个上限。并且这个上限与 a² 成反比，与X围绕其平均值的分散程度成正比，换句话说，与X的方差成正比。从符号上看，Bienaymé-Chebyshev 不等式表示如下：

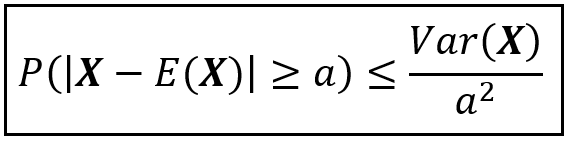
        Bienaymé–Chebyshev 不等式（作者提供图片）

        和马尔可夫不等式一样，比奈梅-切比雪夫不等式的妙处在于它对X的概率分布不做任何假设。X可以是正态分布、指数分布或伽马分布。X可以呈牛影形状分布。比奈梅-切比雪夫概率界限仍然坚如磐石。

4.1 简要回顾Bienaymé–Chebyshev 不等式的历史

        引人入胜的历史为比耶奈梅-切比雪夫不等式的发现提供了素材。首先，在这个不等式中，朱尔斯·比耶奈梅的名字应该排在切比雪夫的名字之前，这是有原因的。

        1853 年，法国数学家 Irénée-Jules Bienaymé 发表了一篇论文，该论文后来成为法国科学院院刊中最重要的论文之一。Bienaymé 的论文表面上是关于他对拉普拉斯最小二乘法的处理。然而，作为这项工作的一部分，他最终陈述并证明了 Bienaymé-Chebyshev 不等式（当时这只能是 Bienaymé 不等式，因为 Chebyshev 根本不存在）。但是，Bienaymé 秉承其谦虚的性格，由于他的注意力完全集中在拉普拉斯最小二乘法上，未能充分说明他的发现的重要性，因此基本上没有引起人们的注意。因此，如果 Pafnuty Lvovich Chebyshev 不是天生腿部萎缩，那么概率领域最重要的结果之一可能就会被遗忘。

        1821 年初夏的一天，25 岁​​的比埃奈梅还在为法国财政部公务员这个职业而努力，帕夫努蒂·利沃维奇·切比雪夫出生在沙皇俄国圣彼得堡以南 100 英里的一个村庄。切比雪夫是家中九个孩子中的一个，从小就表现出了在机械和数学方面的非凡天赋。切比雪夫的父亲是一名军官，他曾在 1812 年拿破仑进攻俄国时击退了拿破仑，而拿破仑的进攻显然是灾难性的（对拿破仑来说）。历史的讽刺之处在于，仅仅两年后，在拿破仑撤退的混乱局面中，朱尔斯·比埃奈梅帮助拿破仑击退了进军巴黎的俄罗斯、奥地利和普鲁士军队。拿破仑当然没能保护好巴黎，反而被流放到厄尔巴岛。

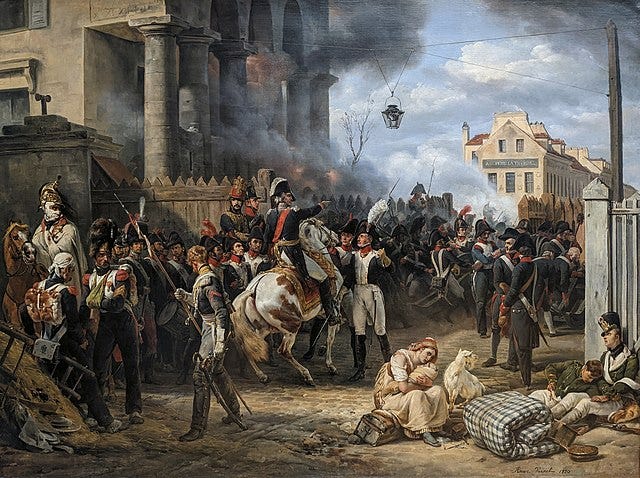
“克利希的巴里埃”。 Défense de Paris, le 30 mars 1814”（克利希屏障。巴黎保卫战，1814 年 3 月 30 日）（艺术家：Horace Vernet）（公共领域艺术品）

所有这些历史在 Pafnuty Lvovich 出生之前就已经上演了 。但考虑到他的军事血统和家族传统，如果不是因为先天性腿部萎缩，PL Chebyshev 很可能会跟随他的一些兄弟姐妹加入沙皇军队，概率史将会发生完全不同的转变。但 Chebyshev 进入数学界以及后来进入俄罗斯学术界并不是他接触 Bienaymé 的唯一催化剂。事实上，他支持后者对 Bienaymé-Chebyshev 不等式的贡献。

小时候，切比雪夫在家里学习法语。在他职业生涯的早期，他似乎意识到，如果他想让自己的作品在国外被人阅读，他就必须在 19 世纪的全球数学研究之都巴黎出名。

一有机会，切比雪夫便前往法国和其他西欧国家的首都，并将 80 篇论文中的近一半发表在西欧期刊上。其中许多论文发表在法国数学家约瑟夫·刘维尔编辑的《Journal des Mathématiques Pures et Appliquées 》（《纯粹与应用数学期刊》）上。正是在 1852 年的欧洲之旅中，切比雪夫被介绍给比埃奈梅，这段互惠互利的友谊使切比雪夫有机会接触到许多欧洲科学家和出版商，后来比埃奈梅自己的数学工作也得到了法国和俄罗斯主要期刊应有的宣传。

当然，最重要的工作是比埃奈梅于 1853 年发现以他的名字命名的不等式。这又把我们带回到对这个不等式的研究。

Bienaymé 在 1853 年的论文中实际证明了以下内容：

假设您要从平均值和方差分别为 μ 和 σ² 的数值总体中抽取一个大小为 N 的随机样本。让X _bar 成为您的随机样本的平均值。顺便说一句，可以证明样本平均值X _bar 本身是一个随机变量，其自身的期望值和方差分别为 μ 和 σ²/N。如果这让您感到困惑，请放心。很快，我将展示如何得出样本平均值的期望值和方差。同时，回到手头的话题，Bienaymé 展示了以下内容：

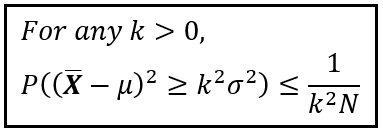
Bienaymé 的结果于 1853 年得到证实（图片来自作者）

现在，您可能想知道切比雪夫究竟何时进入比耶奈梅 (Bienaymé) 发现的快乐轨道，从而导致切比雪夫的名字与这个不等式联系在一起。

巧合的是，在 Bienaymé 发表不等式 14 年后，Chebyshev 完全不知道 Bienaymé 的发现，在 1867 年出版的 Joseph Liouville 期刊上发表了该不等式的另一个版本。请记住，这是 Google、CiteSeer 和电话出现之前的时代。因此，说当时的科学家没有充分了解“先前的研究”几乎不能说明问题的严重性。

无论如何，切比雪夫版本的不等式适用于N 个独立但不一定相同分布的随机变量X 1, X 2, X 3, …, X N 的平均值X _bar 。刘维尔似乎知道比奈梅的工作，他精明地在其 1867 年出版的期刊上重新发表了比奈梅 1853 年的论文，并将其放在切比雪夫的论文之前！

《Journal de Mathématiques Pures et Appliquées》（《纯粹数学与应用数学杂志》）目录，Liouville，(2) 12 158–176.（1867 年）（公共领域问题）

值得赞扬的是，切比雪夫在 1874 年发表的一篇论文中将这个不等式的发现完全归功于 Bienaymé：

“在我的笔记《平均价值》中，可以找到对伯努利定律的简单而严格的证明，这只是从 M. Bienaymé 的方法中轻松推导出的结果之一，这种方法使他自己证明了一个概率定理，伯努利定律由此直接得出”

在随后的几年中，人们提出了切比雪夫不等式（或更准确地说，比奈梅 —切比雪夫不等式），它适用于任何具有预期值 E( X ) 和有限方差 Var( X ) 的随机变量X。

Bienaymé — Chebyshev 不等式指出，对于任何正“a”，概率 P(| X — E( X | ≥ a) 有界如下：

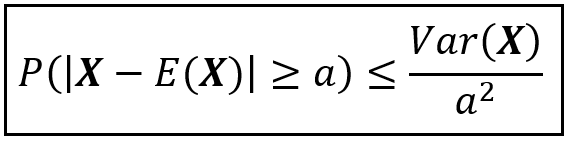
Bienaymé–Chebyshev 不等式（作者提供图片）

4.2 Bienaymé — Chebyshev 不等式的证明

马尔可夫在 1913 年出版的《概率论与计算》一书中证明了不等式（并以他的名字命名），该不等式通常用于证明 Bienaymé — Chebyshev 不等式。使用马尔可夫不等式作为起点，证明结果轻而易举。我们将其证明如下：

假设一个随机变量X，其均值为 E( X )。现在，我们定义另一个随机变量Z = ( X — E( X ))²。平方项确保Z为非负数，这样我们就可以将马尔可夫不等式应用于Z。假设Z有一个阈值，我们称之为 a²。Z 的观测值达到或超过 a² 的概率为 P( Z >= a²)。将马尔可夫不等式应用于Z和 a² 可得出以下结论：

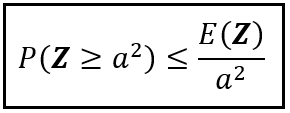
使用马尔可夫不等式计算P( Z≥a² )的上限（作者提供图片）

从上述表达式开始，我们可以推导出如下的 Bienaymé-Chebyshev 不等式：

以马尔可夫不等式为起点推导比奈梅-切比雪夫不等式（图片来自作者）

方程 (3) 是Bienaymé-Chebyshev 不等式（或简称为 Chebyshev 不等式）。

除了使用任意阈值“a”之外，还可以用X的标准差 σ 来表示“a”，如下所示：

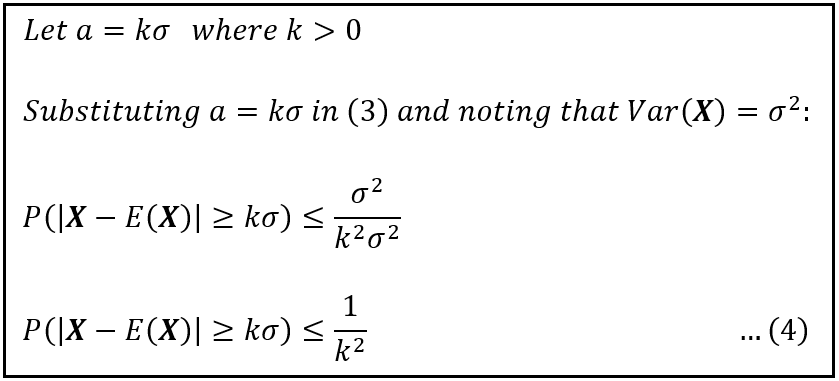
用X的标准差表示的 Bienaymé-Chebyshev 不等式（作者提供的图片）

上述证明也为 Bienaymé 在 1853 年出版的论文中给出的原始结果的证明提供了直接的途径，即：

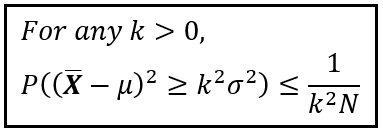
Bienaymé 的结果于 1853 年得到证实（图片来自作者）

从方程 (2) 开始，用样本平均值X _bar代替X，用 k²σ² 代替 a²，我们得出 Bienaymé 于 1853 年左右得出的结果，如下所示：

Bienaymé 在 1853 年证明的结果的推导（图片来自作者）

方程 (4) 和 (4a) 向我们展示了一个有趣的结果。它们表明，遇到距离平均值至少有 k 个标准差的观测值的概率有一个上限，并且这个上限与 k² 成反比。

换句话说，人们极不可能遇到与平均值相差几个标准差的值。

当用这种方式表达时，比奈梅-切比雪夫不等式就为这样的格言“如果听起来好得令人难以置信，那么它很可能就是假的”或科学家们一直以来最喜欢的那句格言“非凡的主张需要非凡的证据”赋予了数学的面孔。

为了说明这种不等式的作用，请考虑以下数据集，该数据集是每年 1 月 1 日在芝加哥地区记录的平均每日气温。从 1924 年到 2023 年共有 100 个观测值：

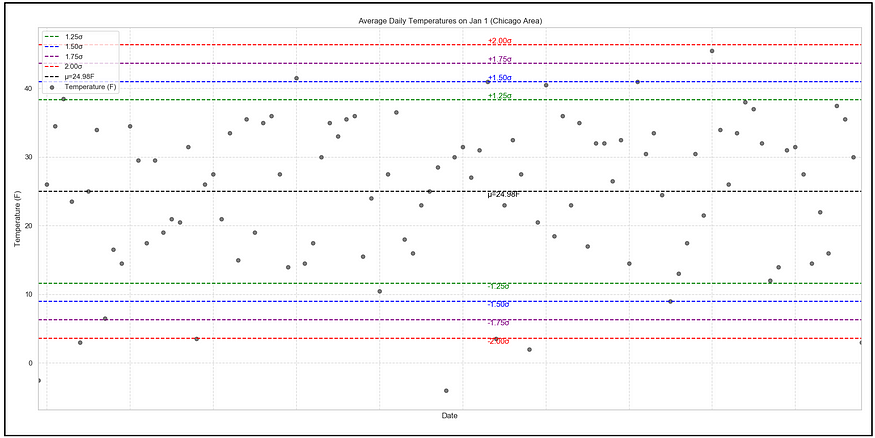
1924 年至 2023 年每年 1 月 1 日芝加哥地区的平均每日气温（图片来自作者）（数据来源：NWS，公共领域许可）

图表中心的黑色虚线水平线表示样本平均值 24.98 F。彩色水平线表示数据样本标准偏差的正负 1.25、1.5、1.75 和 2 倍的温度值。这些标准偏差线让我们感受到大多数温度可能处于的范围内。

应用 Bienaymé–Chebyshev 不等式，我们可以确定概率 P(| X — E( X )| ≥ kσ)的上限，其中X表示随机选择的年份中 1 月 1 日的观测平均温度。E( X ) = 24.98 F，σ = 10.67682 F，k = 1、1.25、1.5、1.75 和 2.0。下表在 1/k² 列中提到了这些概率界限：

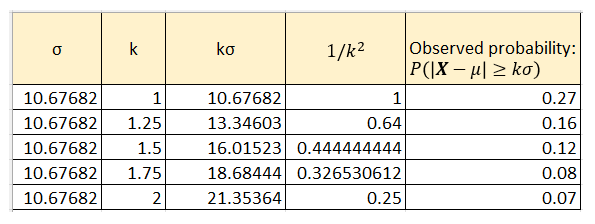
对于芝加哥气温数据集，使用 Bienaymé–Chebyshev 不等式计算的概率 P(| X -E(X)| ≥ kσ)的上限，以及数据样本中相应的观测概率。（图片来自作者）

表格的最后一列显示了在数据样本中观察到此类偏差的实际概率。数据样本中的实际观测值恰好在 Bienaymé-Chebyshev 不等式生成的概率范围内。

您可能已经注意到，Bienaymé–Chebyshev 不等式生成的概率边界相当宽。例如，当 k=1（对应于事件位于平均值的 1 个标准差内）时，不等式计算出的概率上限为 1/1² = 1.0，即 100%。这使得这个特定的边界实际上毫无用处。

尽管如此，对于所有 k > 1 的值，该不等式都非常有用。它的用处还在于它不假设随机变量的分布有任何特定的形状。事实上，它的适用性甚至更进一步。虽然马尔可夫不等式要求随机现象产生严格非负的观测值，但如果你注意到，Bienaymé-Chebyshev 不等式对X并没有做出这样的假设。

Bienaymé–Chebyshev 不等式还为我们提供了弱大数定律的简单证明。事实上，1913 年，马尔可夫在他的概率论著作中使用了这个不等式来证明弱大数定律，而这基本上与当今许多教科书使用的证明相同。

五、弱大数定律（及其证明）

5.1 定律陈述

        假设您从理论上无限大的总体中收集一个随机样本。假设样本大小为 N。此随机样本的样本均值为X _bar。由于您处理的只是一个样本，而不是整个总体，因此您的样本均值可能与真实总体均值 μ 相差一定距离。这就是样本均值的误差。您可以将此误差的绝对值表示为 | X _bar — μ|。

        WLLN 表示，对于您选择的任何正公差 ϵ，当样本大小 N 增长到无穷大时，样本平均值中误差大于 ϵ 的概率将缩小到零。您选择的公差 ϵ 有多小并不重要。当样本大小 N 趋近于无穷大时，P(| X _bar — μ| >= ϵ) 将趋近于零。

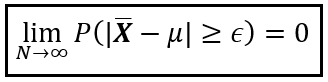
弱大数定律（作者提供图片）

        WLLN 有着丰富的发现历史，可以追溯到三个多世纪以前，数学界的名人都为其发展做出了贡献——从 1713 年的雅各布·伯努利开始，包括棣莫弗、拉普拉斯、拉克鲁瓦、泊松以及我们的朋友比奈梅和切比雪夫等巨人。由于比奈梅-切比雪夫不等式的存在，WLLN 的证明就像山坡上的水一样容易。

5.2 弱大数定律的证明

        与统计学中的许多事物一样，我们首先从总体中抽取一个大小为 N 的随机样本来证明。我们将此样本表示为X 1、X 2、X 3、...、X N。将 X 1、X 2、X 3、...、X N 视为一组 N 个变量（就像一组 N 个槽）很有用，每当抽取一个样本时，每个槽都会从总体中随机选择的值进行填充。因此，X 1、X 2、X 3、...、X N本身就是随机变量。此外，由于 X 1、X 2、X 3、...、X N 中的每一个都获得一个独立于其他变量的随机值，但都来自样本总体，因此它们是独立的、同分布的(iid) 随机变量。

        对于任何给定的随机选择的样本，样本平均值X _bar 可以按如下方式计算：

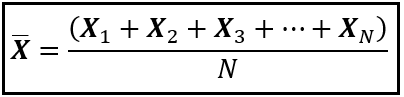
        样本均值（作者提供图片）

        由于抽取另一个随机样本将产生不同的样本均值，而抽取第三个样本将产生另一个样本均值，依此类推，样本均值X _bar 本身是一个具有自身均值和方差的随机变量。让我们计算 X_bar 的均值。

        样本均值的期望值的推导（图片来自作者）

        我们还来计算样本均值的方差。

        样本均值的方差等于总体方差除以 N（作者提供的图片）

        现在我们将 Bienaymé-Chebyshev 不等式应用于样本均值X _bar ，如下所示：

        使用 Bienaymé–Chebyshev 不等式证明弱大数定律（作者提供图片）

        像 WLLN 这样意义深远、影响深远且对统计科学领域如此重要的事物，怎么会有如此简单易懂的证明，这真是大自然的荒谬之处，让人惊叹不已。无论如何，这就是事实。

        综合起来，马尔可夫不等式、比奈梅-切比雪夫不等式和弱大数定律构成了大量统计科学的坚实基础。例如，当您训练统计模型（或神经网络模型）时，训练算法最好遵循 WLLN。如果不遵循，系数估计就不能保证收敛到真实的总体值。这使得您的训练技术基本上毫无用处。WLLN 还在另一个史诗般的结果——中心极限定理的证明中找到了有报酬的就业机会。而这理所当然地将成为我下一篇文章的主题。