摩尔投票法，又称为博耶-摩尔多数投票算法，是一种用于在一组数据中寻找多数元素(出现次数超过一半的元素)的算法。该算法的效率非常高，时间复杂度为O(n)，空间复杂度为O(1)，适合处理大数据量的情况。

步骤

首先定义两个变量candidate,count。

从数组中任选一个元素作为候选元素（candidate），并初始化计数（count）为1。

遍历数组：遇到与candidate相同的元素，count++,遇到不同的元素，count--.

若count减到0，更换candidate为当前元素，并将count重置为1。

遍历结束：candidate即为多数元素

示例

以数组 { 1 2 7 9 2 2 2 2 7  }  为例

 我们选取第一个数字为candidate。count为0；

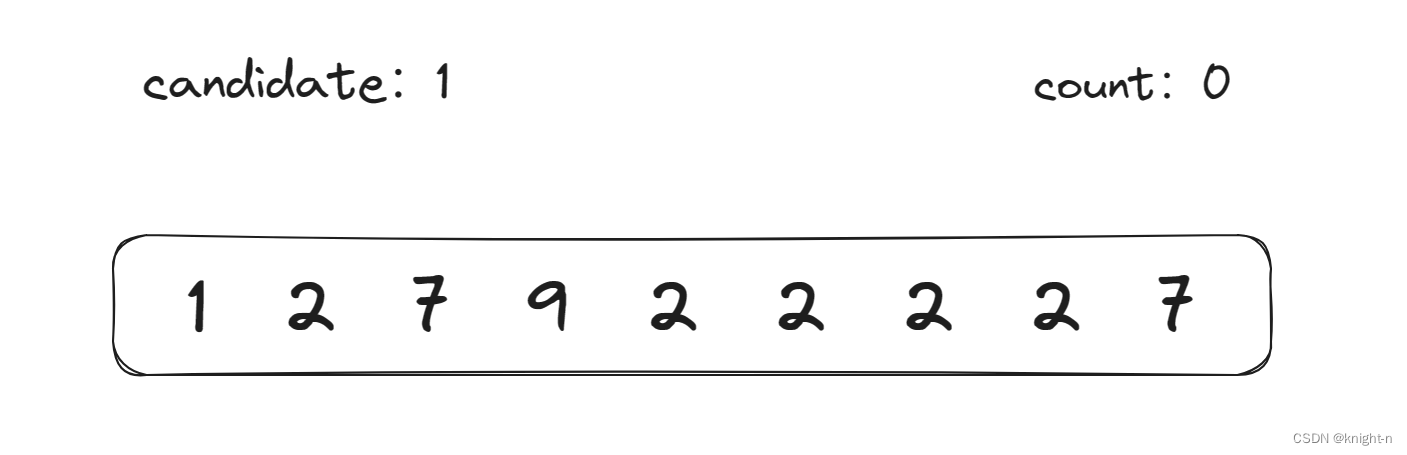
 遍历数组：

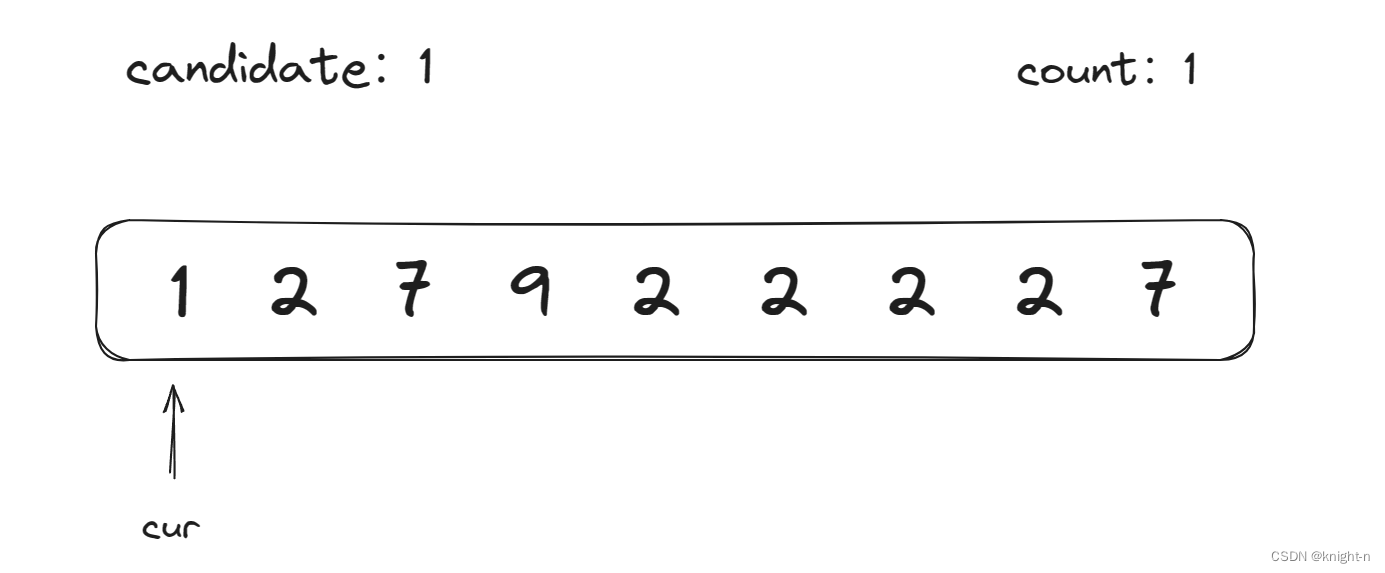
当前数字为1，等于candidate，count++，向后遍历。

当前数字为2，不等于candidate，count--，count==0，candidate更新为2，count更新为1。向后遍历。 

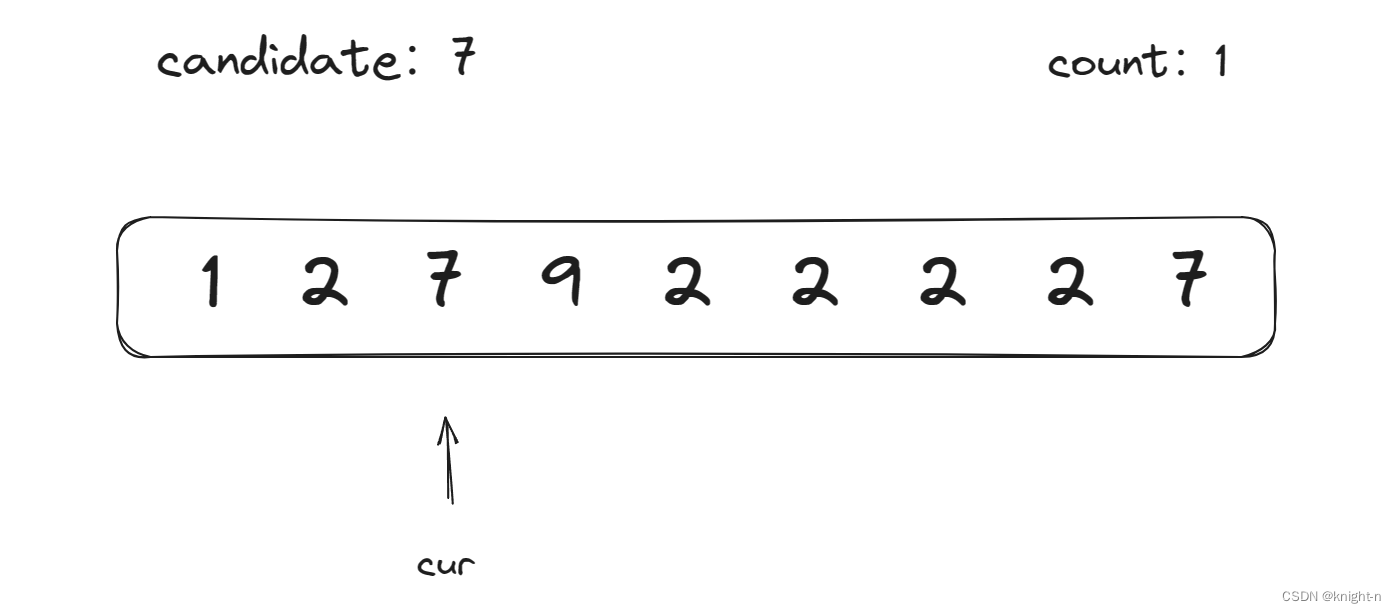
当前数字为7，不等于candidate，count--，count==0，candidate更新为7，count更新为1。向后遍历。

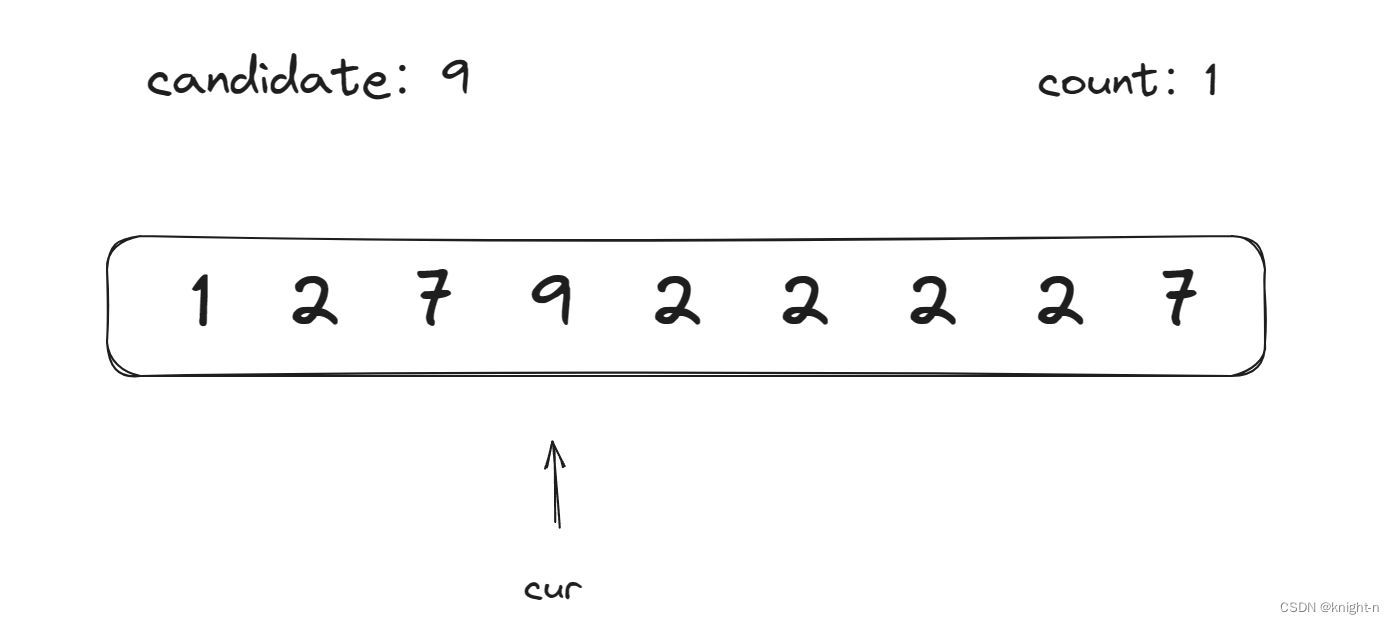
当前数字为9，不等于candidate，count--，count==0，candidate更新为9，count更新为1。向后遍历。

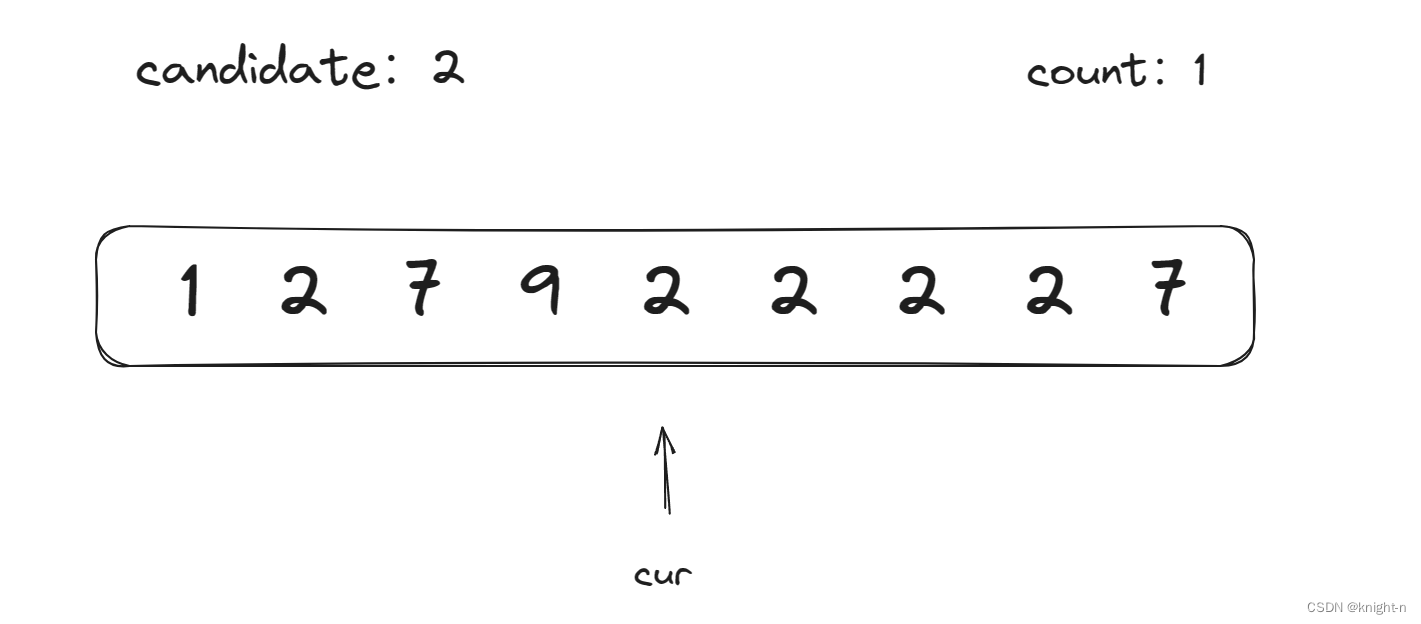
当前数字为2，不等于candidate，count--，count==0，candidate更新为2，count更新为1。向后遍历。 

当前数字为2，等于candidate，count++，count==2，向后遍历。  

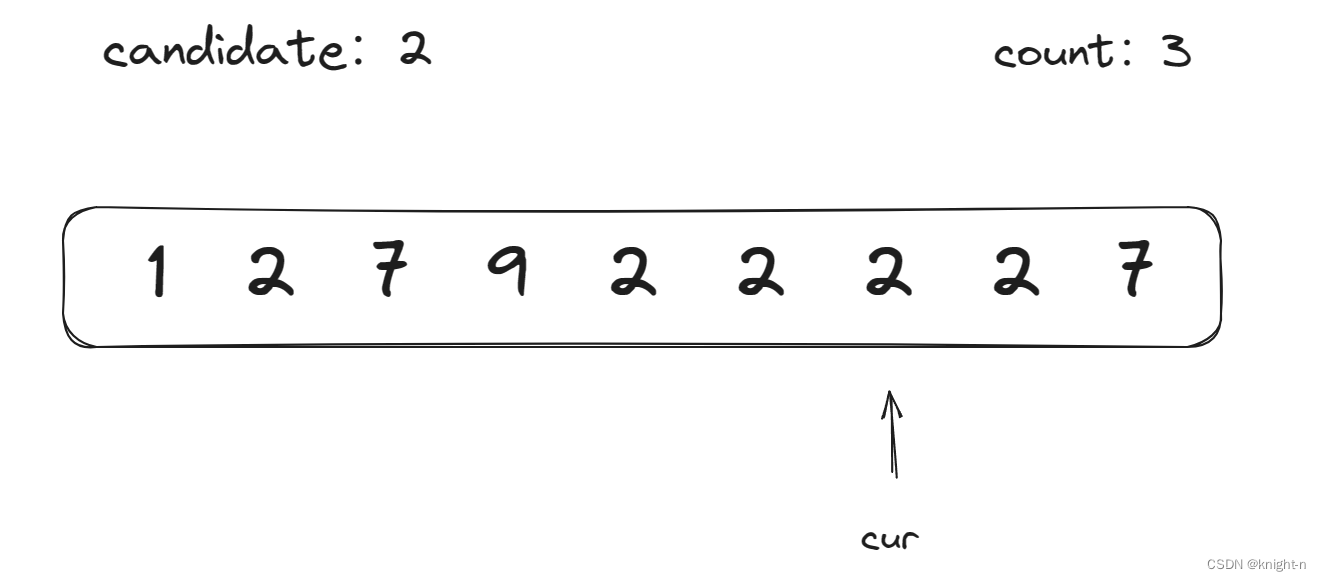
当前数字为2，等于candidate，count++，count==3，向后遍历。   

当前数字为2，等于candidate，count++，count==4，向后遍历。    

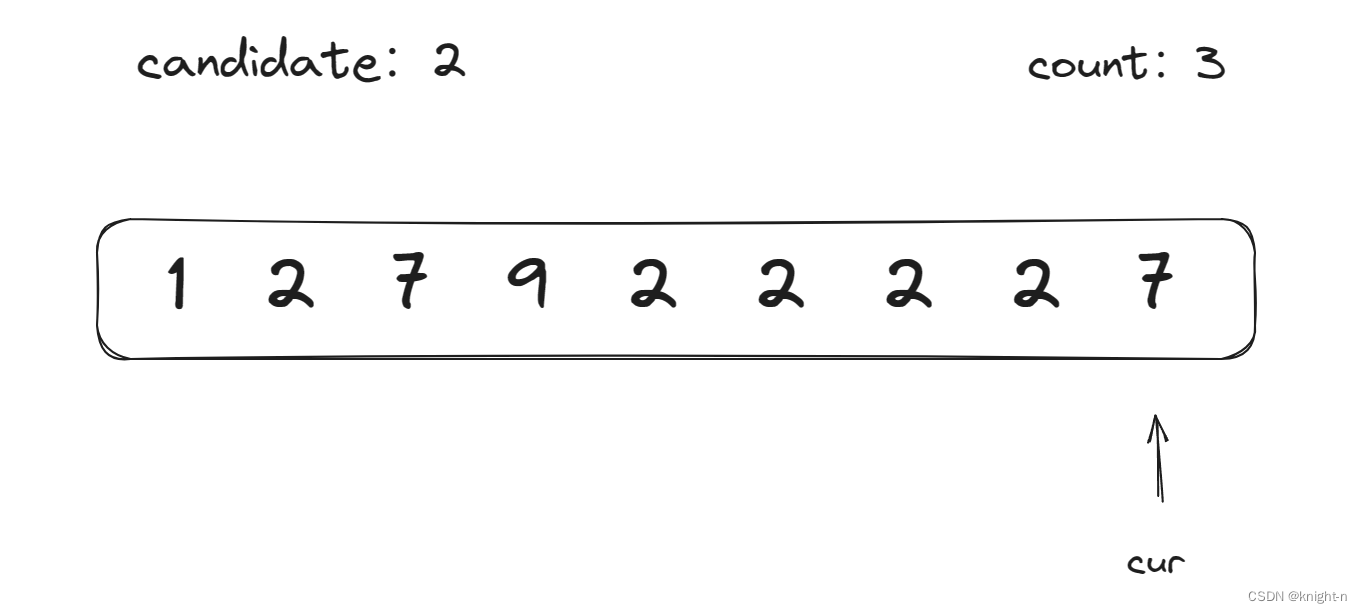
当前数字为9，不等于candidate，count--，count==3，不更新，遍历结束。多数元素为2。 

原理

摩尔投票法的基本原理是让不同元素相互抵消，我们可以将所有与当前候选元素相同的元素视为支持者投支持票即count++，其他元素投反对票即count--。

当count减到0时，意味着当前候选元素已经没有多数优势，因为它与其它元素的反对票相等。

这时，将当前遍历到的元素设置为新的候选元素，并将计数器count重置为1。这个新元素成为新的暂时多数元素，开始累积新的支持票。

为什么有效

由于多数元素在数组中出现的次数超过一半，即便在遍历过程中不断遇到与当前候选元素不同的元素导致计数器减小，多数元素最终能够持续保持“支持票”领先，不会被完全抵消。

 代码实现

int majorityElement(vector<int>& nums) 
{
    int count = 0,andidate = nums[0];
    for(auto& e: nums)
    {
        if(e==andidate)
            count++;
        else
            count--;
        if(!count)
        {
            andidate=e;
            count=1;
        }
    }
    return andidate; 
}

检验：169. 多数元素