本节博客是通过——二位前缀和模板题来介绍前缀和二维算法，有需要借鉴即可。

1.题目

题目链接：LINK

2.暴力求解

这里我们首先想到的就是一个暴力求解的方式，挨个需要的进行遍历就好了嘛~代码很简单，反正八成这牛客不会让你过。。。这里我们就不再赘述了。

3.二维前缀和算法

想一想，我们暴力求解的时间复杂度直接升到(NMQ)了，之所以能上到这个复杂度无非就是算过的数据没记住，第二次一样的数据还是去重新计算重新计算。

到了这个想法，我们可以想到“以空间换时间”的思路去处理这道题。也就是说我们可以借用“二维前缀和算法”来进行求解。

具体步骤如下

• 1.预处理一个前缀和数组出来：
  
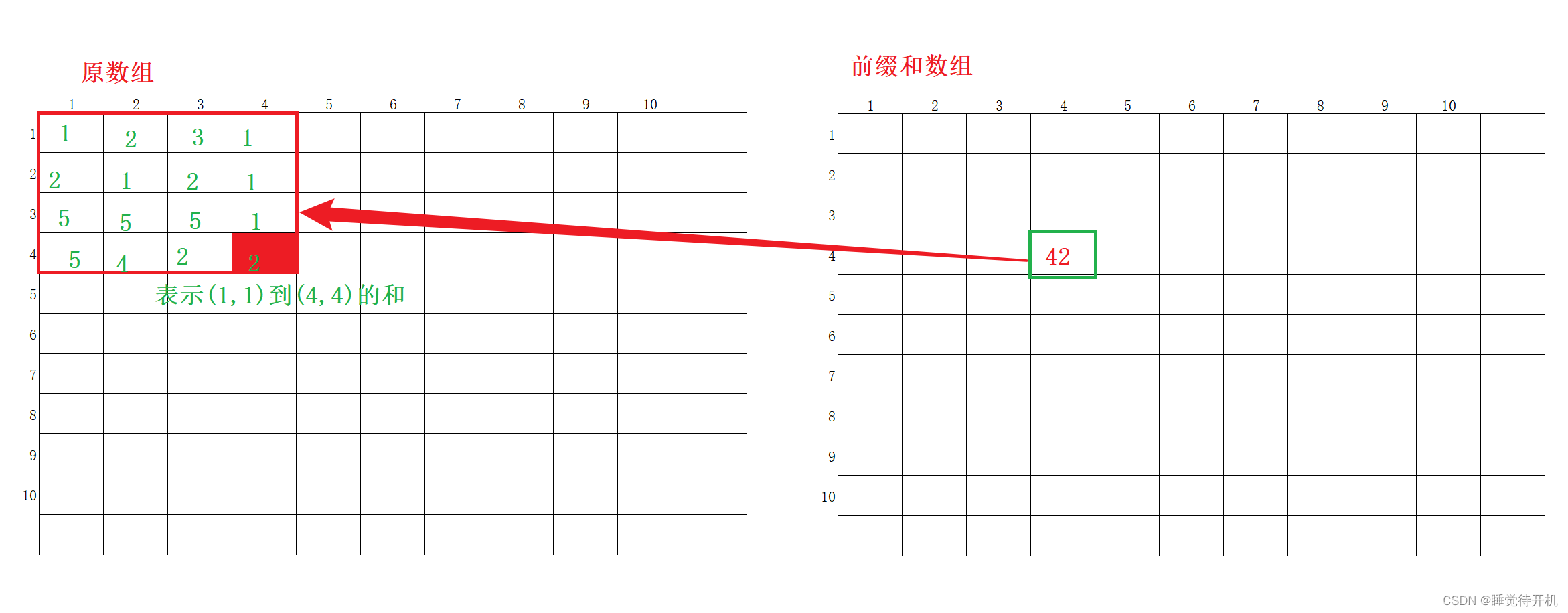
  所以，这个前缀和数组满足下列规律：
  

• 2.依据相关规律来利用预处理出来的前缀和数组来进行处理：
  任何一个所求结果，均满足下面规律：
  

这样下来，我们就可以写出下面代码了：

3.代码示例

#include <iostream>
using namespace std;
#include<vector>

int main() 
{
    // 1.读入参数
    int n = 0, m = 0, q = 0;
    cin >> n >> m >> q;
    vector<vector<int>> vv(n+1, vector<int>(m+1));
    for(size_t i = 1; i <= n; i++)
    {
        for(size_t j = 1; j <= m; j++)
        {
            cin >> vv[i][j];
        }
    }
    // 2.预处理二维前缀和数组
    vector<vector<long long>> dp(n+1, vector<long long>(m+1));
    for(size_t i = 1; i <= n; i++)
    {
        for(size_t j = 1; j <= m; j++)
        {
            dp[i][j] = dp[i-1][j] + dp[i][j-1] + vv[i][j] - dp[i-1][j-1];
        }
    }
    // 3.求值
    int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
    while(q--)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;
    }
}
// 64 位输出请用 printf("%lld")

4.总结

这个题目二位前缀和算法的这个公式推导过程比较重要，建议自己梳理一下。
整体上是一个“以空间换时间”的思路。

---

EOF