图_基础算法

图这种数据结构还有一些比较特殊的算法，比如二分图判断，有环图无环图的判断，拓扑排序，以及最经典的最小生成树，单源最短路径问题，更难的就是类似网络流这样的问题。

先看拓扑排序（有环无环）：la总微信文章的链接：https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247491897&idx=1&sn=c2d77dd649548d077815af3c976b61d1&scene=21#wechat_redirect
然后看二分图
然后看并查集
然后最小生成树dijkstra 单源最短路径

基本概念：

大部分都是以邻接表的形式存储：

// 记得每一个都要初始化一下为new ArrayList<>()或者LinkedList;
List<Integer>[] graph;

拓扑排序

拓扑排序的对象，就是有向无环图（DAG）。一个有向无环图的拓扑排序结果不止一种。

给定一个包含 n个节点的有向图 G，我们给出它的节点编号的一种排列，如果满足：

对于图 G 中的任意一条有向边 (u,v)，u 在排列中都出现在 v的前面。

那么称该排列是图 G 的「拓扑排序」

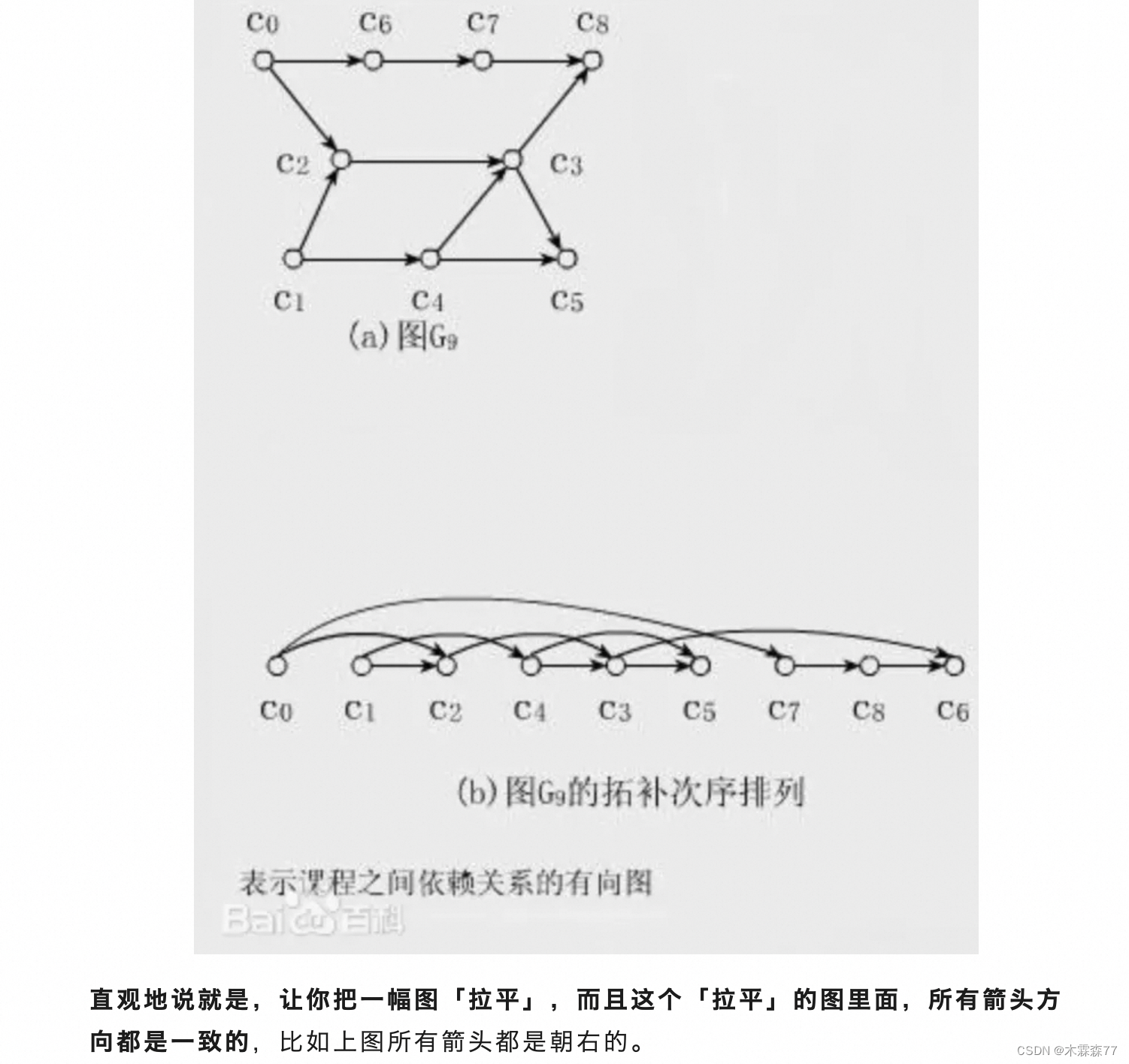
在这里插入图片描述

先说一下怎么判断图有没有环（力扣207 课程表）。
BFS很简单，直接把所有入度为0的入队列遍历一遍，adj度数减1，要是入度为0就继续入队列，最后还有度数不为0的节点（也可以每次遍历queue计数，最后判断计数结果等不等于n），就说明有环。

// 207题 BFS实现
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int[] indegrees = new int[numCourses];
        List<List<Integer>> adjacency = new ArrayList<>();
        Queue<Integer> queue = new LinkedList<>();
        // 初始化图
        for(int i = 0; i < numCourses; i++)
            adjacency.add(new ArrayList<>());
        // 注意cp[0]前置为cp[1]，所以先上cp[1]才能继续走到cp[0]，即 箭头指向为1->0
        for(int[] cp : prerequisites) {
            indegrees[cp[0]]++;
            adjacency.get(cp[1]).add(cp[0]);
        }
        // 把所有入度为0的加进来
        for(int i = 0; i < numCourses; i++)
            if(indegrees[i] == 0) queue.add(i);
        // 开始bfs
        while(!queue.isEmpty()) {
            int pre = queue.poll();
            numCourses--;
            for(int cur : adjacency.get(pre))
            // 别忘了减入度
                if(--indegrees[cur] == 0) queue.add(cur);
        }
        // 根据n是否减为0判断是否全部节点都被遍历了一遍，如果有环就说明n不为0
        return numCourses == 0;
    }
}

dfs判断的方式更简单了，在开始进入遍历cur的adj之前 标记onPath为true，遍历完adj之后把onPath恢复为false（恢复现场）。下一次递归开始时发现onPath已经为true就说明有环，类似贪吃蛇咬到了自己。
onPath数组和visited数组可以合为一个数组，用int标识不同的情况。例如初始化flag数组都是0，然后进入递归置为1，结束递归置为-1.这样，每次进入一个节点的时候就判断如果flag==-1就返回；flag为1就说明有环。

// DFS判断是否有环
boolean[] onPath;

boolean hasCycle = false;
boolean[] visited;

void traverse(List<Integer>[] graph, int curIndex) {
    if (onPath[curIndex]) {
        // 发现环！！！
        hasCycle = true;
    }
    if (visited[curIndex]) {
        return;
    }
    // 将节点 s 标记为已遍历
    visited[curIndex] = true;
    // 开始遍历节点 s
    onPath[curIndex] = true;
    for (int adj : graph[curIndex]) {
        traverse(graph, adj);
    }
    // 节点 s 遍历完成
    onPath[curIndex] = false;
}

注意由于可能一次traverse并不能遍历完所有的节点，所以要遍历nums，从0-n都当成curIndex传入。

// 207课程表 dfs实现判断是否有环，以flag为标识 return true或者false
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<List<Integer>> adjacency = new ArrayList<>();
        for(int i = 0; i < numCourses; i++)
            adjacency.add(new ArrayList<>());
        int[] flags = new int[numCourses];
        for(int[] cp : prerequisites)
            adjacency.get(cp[1]).add(cp[0]);
        for(int i = 0; i < numCourses; i++)
            if(!dfs(adjacency, flags, i)) return false;
        return true;
    }
    private boolean dfs(List<List<Integer>> adjacency, int[] flags, int i) {
        if(flags[i] == 1) return false;
        if(flags[i] == -1) return true;
        flags[i] = 1;
        for(Integer j : adjacency.get(i))
            if(!dfs(adjacency, flags, j)) return false;
        flags[i] = -1;
        return true;
    }
}

然后借机说一下递归怎么进行拓扑排序，以力扣的210课程表II 为例，由于有依赖的前置课程，所以我们要先完成依赖的课程，也就是树的根节点。再代入后序遍历的思路，拓扑排序的结果其实就是这个多叉树后序遍历的数组反转之后的结果。
当然，如果要实现拓扑排序，前提一定是要先判断是否有环的。可以在遍历的时候判断，也可以直接把207的代码copy过来

boolean[] visited;
// 记录后序遍历结果
List<Integer> postorder = new ArrayList<>();

int[] findOrder(int numCourses, int[][] prerequisites) {
    // 先保证图中无环
    if (!canFinish(numCourses, prerequisites)) {
        return new int[]{};
    }
    // 建图
    List<Integer>[] graph = buildGraph(numCourses, prerequisites);
    // 进行 DFS 遍历
    visited = new boolean[numCourses];
    for (int i = 0; i < numCourses; i++) {
        traverse(graph, i);
    }
    // 将后序遍历结果反转，转化成 int[] 类型
    Collections.reverse(postorder);
    int[] res = new int[numCourses];
    for (int i = 0; i < numCourses; i++) {
        res[i] = postorder.get(i);
    }
    return res;
}

void traverse(List<Integer>[] graph, int s) {
    if (visited[s]) {
        return;
    }

    visited[s] = true;
    for (int t : graph[s]) {
        traverse(graph, t);
    }
    // 后序遍历位置
    postorder.add(s);
}

为什么310的最小高度树的解法（把入度为1也就是叶子结点入队列然后每次去掉一圈叶子结点之后就是根节点了）是拓扑排序，可能是因为满足拓扑排序的性质：后序遍历。

并查集 Union-Find

并查集比较简单，也可以直接用并查集判断是否有环，这里直接附上并查集的代码

class UF {
            private int count;
            private int parent[];

            public UF(int n) {
                parent = new int[n+1];
                // 初始化的时候 全都是独立的根节点 指向自己
                for (int i = 0; i <= n; i++) {
                    parent[i] = i;
                }
                // 计数count
                count = n;
            }

            public int getUFCount() {
                return count;
            }

            public int findRoot(int x) {
                // 注意回溯的话要用if。循环的话要用while
               if (parent[x] != x) {
                    parent[x] = findRoot(parent[x]);
                }
                return parent[x];
                /*while (parent[x] != x) {
                    // 进行路径压缩
                    parent[x] = parent[parent[x]];
                    x = parent[x];
                }
                return x;*/
            }

            public void union(int a, int b) {
                int rootA = findRoot(a);
                int rootB = findRoot(b);
                if (rootA == rootB) {
                    return;
                }
                parent[rootA] = rootB;

                // 别忘了count--
                count--;
            }

            public boolean connected(int a, int b) {
                return findRoot(a) == findRoot(b);
            }
        }

并查集相关题目：
785 判断二分图
1319 连通网络的操作次数这题用UF做可以；用DFS类似于判断拓扑排序是否有环也可以，具体看一下题解。
886 可能的二分法

在这里插入图片描述

二分图

接着说一下二分图

定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为二分图。

二分图也可以用并查集UF来解决，把所有cur的adj都union,遍历某个adj的时候如果发现adj和cur已经相连了connected了，就说明不可分为两个独立子集。
例题：785 判断二分图
还有一种就是染色法，遍历adj如果未染色就染成和cur不一致的颜色，如果发现adj颜色不是初始状态且和cur颜色一致，就说明不可二分。

染色可以初始化RED/BLUE之类的，也可以直接用int标识。例如0；1；-1

/**
         * BFS广度优先遍历-染色法
         *
         * @param graph
         * @return
         */
        private boolean useBfs(int[][] graph) {
            int n = graph.length;
            Deque<Integer> queue = new ArrayDeque<>(n);

            // 用visit数组表示染色，visited[i]为0表示还未被染色，初次染色为1，其邻接点染色时被赋值为-1
            int visited[] = new int[n];
            // 每个节点未被染色前都要进队列
            for (int i = 0; i < n; i++) {
                if (visited[i] != 0) {
                    continue;
                }
                visited[i] = 1;
                queue.addLast(i);
                while (!queue.isEmpty()) {
                    int item = queue.removeFirst();
                    for (int adj : graph[item]) {
                        // 未被染色 就处理为-visited[item];
                        if (visited[adj] == 0) {
                            visited[adj] = -visited[item];
                            queue.addLast(adj);
                        }
                        // 已被染色且和当前颜色相等 就返回false
                        else if (visited[adj] == visited[item]) {
                            return false;
                        }
                    }
                }
            }
            return true;
        }

最小生成树

Kruskal 算法

一开始的时候就把所有的边排序，然后从权重最小的边开始挑选属于最小生成树的边，组建最小生成树。

prim算法

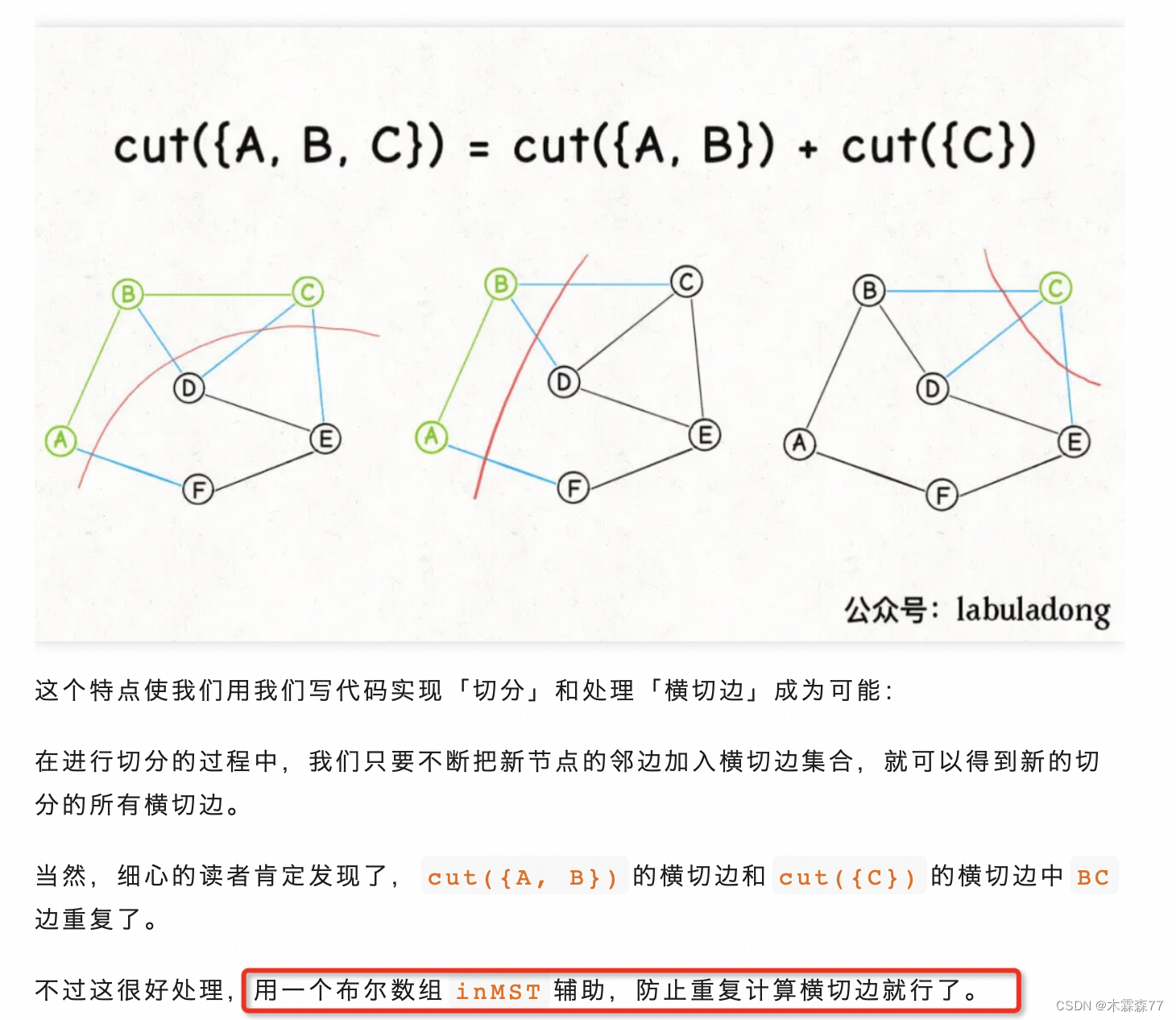
原理：对于任意一个节点，切分他的连接点之后，横切边上权重最小的边，一定是构成最小生成树的一条边。
实现：用优先级队列结合BFS动态获取权重最小边
为了防止重复切，需要用一个变量判断是否已经被加入过结果集（最小生成树）中了。
在这里插入图片描述

class Prim {
    // 核心数据结构，存储「横切边」的优先级队列
    private PriorityQueue<int[]> pq;
    // 类似 visited 数组的作用，记录哪些节点已经成为最小生成树的一部分
    private boolean[] inMST;
    // 记录最小生成树的权重和
    private int weightSum = 0;
    // graph 是用邻接表表示的一幅图，
    // graph[s] 记录节点 s 所有相邻的边，
    // 三元组 int[]{from, to, weight} 表示一条边
    private List<int[]>[] graph;

    public Prim(List<int[]>[] graph) {
        this.graph = graph;
        this.pq = new PriorityQueue<>((a, b) -> {
            // 按照边的权重从小到大排序
            return a[2] - b[2];
        });
        // 图中有 n 个节点
        int n = graph.length;
        this.inMST = new boolean[n];

        // 随便从一个点开始切分都可以，我们不妨从节点 0 开始
        inMST[0] = true;
        cut(0);
        // 不断进行切分，向最小生成树中添加边
        while (!pq.isEmpty()) {
            int[] edge = pq.poll();
            int to = edge[1];
            int weight = edge[2];
            if (inMST[to]) {
                // 节点 to 已经在最小生成树中，跳过
                // 否则这条边会产生环
                continue;
            }
            // 将边 edge 加入最小生成树
            weightSum += weight;
            inMST[to] = true;
            // 节点 to 加入后，进行新一轮切分，会产生更多横切边
            cut(to);
        }
    }

    // 将 s 的横切边加入优先队列
    private void cut(int s) {
        // 遍历 s 的邻边
        for (int[] edge : graph[s]) {
            int to = edge[1];
            if (inMST[to]) {
                // 相邻接点 to 已经在最小生成树中，跳过
                // 否则这条边会产生环
                continue;
            }
            // 加入横切边队列
            pq.offer(edge);
        }
    }

    // 最小生成树的权重和
    public int weightSum() {
        return weightSum;
    }

    // 判断最小生成树是否包含图中的所有节点
    public boolean allConnected() {
        for (int i = 0; i < inMST.length; i++) {
            if (!inMST[i]) {
                return false;
            }
        }
        return true;
    }
}

dijkstra最短路径

说到了这里，狄杰斯特拉算法其实非常简单，就是一个BFS算法的进阶使用，先用一个对象State保存当前节点ID、距离start节点的距离distFromStart。每次用优先级队列，按照distFromStart从小到大排序。然后遍历队列中cur的adj，把最小路径加入结果集中即可。

// 返回节点 from 到节点 to 之间的边的权重
int weight(int from, int to);

// 输入节点 s 返回 s 的相邻节点
List<Integer> adj(int s);

// 输入一幅图和一个起点 start，计算 start 到其他节点的最短距离
int[] dijkstra(int start, List<Integer>[] graph) {
    // 图中节点的个数
    int V = graph.length;
    // 记录最短路径的权重，你可以理解为 dp table
    // 定义：distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
    int[] distTo = new int[V];
    // 求最小值，所以 dp table 初始化为正无穷
    Arrays.fill(distTo, Integer.MAX_VALUE);
    // base case，start 到 start 的最短距离就是 0
    distTo[start] = 0;

    // 优先级队列，distFromStart 较小的排在前面
    Queue<State> pq = new PriorityQueue<>((a, b) -> {
        return a.distFromStart - b.distFromStart;
    });

    // 从起点 start 开始进行 BFS
    pq.offer(new State(start, 0));

    while (!pq.isEmpty()) {
        State curState = pq.poll();
        int curNodeID = curState.id;
        int curDistFromStart = curState.distFromStart;

        if (curDistFromStart > distTo[curNodeID]) {
            // 已经有一条更短的路径到达 curNode 节点了
            continue;
        }
        // 将 curNode 的相邻节点装入队列
        for (int nextNodeID : adj(curNodeID)) {
            // 看看从 curNode 达到 nextNode 的距离是否会更短
            int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
            if (distTo[nextNodeID] > distToNextNode) {
                // 更新 dp table
                distTo[nextNodeID] = distToNextNode;
                // 将这个节点以及距离放入队列
                pq.offer(new State(nextNodeID, distToNextNode));
            }
        }
    }
    return distTo;
}

这里有一个优化点，不用visited数组判断是否会走回头路，因为每个adj都先判断加上cur-adj的权重之后是否小于之前已加入结果集的最小路径，小的话才会更新结果集并加入队列。
因为两个节点之间的最短距离（路径权重）肯定是一个确定的值，不可能无限减小下去，所以队列一定会空，不会无限循环。队列空了之后，distTo数组中记录的就是从start到其他节点的最短距离。

上述代码是为了找到从start到所有节点的最小路径（结果集为distTo[]），如果指定了到end节点，在while循环中判断curNodeId==end即可结束while循环,return curDistFromStart（因为每次从优先级队列中拿出来的一定是最小的路径权重）。

相关题目：
743 题「网络延迟时间
第 1514 题「概率最大的路径」

看一下1631 最小体力消耗路径应该和并查集、二分、dijkstra最短路径都有关系