异相(相位不平衡)状态下的合成器效率分析-理论与ADS仿真
12、ADS使用记录之功分器设计中简单介绍了威尔金森功分器的设计方法。一般来讲,功分器反过来就能作为合路器使用,在输入信号相位一致的情况下,各种合路器的效率指标往往都不错。尤其是威尔金森功分器,在高效率合路的同时还能实现多个输入端口间的隔离。
但是,对于输入信号相位不一致的情况,合路效率是怎么样的呢?在此分别对威尔金森功分器、T功分器在异相(相位不平衡)下的合路效率性能进行分析。
实际上,将两路相位不同的信号进行合路是一种罕见情况,一个典型运用是,Outphasing放大器需要使用此异相合路网络实现对调制信号的高效率放大。Chireix功率合成器是此过程中较为常用的合成方法,这个之后再详细分析。
文中推导部分参考的是”基于高效率功率放大器的数字Outphasing 发射机研究与设计“的第四章,但是其中非隔离T功分器的效率推导有误,在本文中更正了。
本文的工程下载:异相(相位不平衡)状态下的合成器效率分析-理论与ADS仿真工程文件
目录
- 异相(相位不平衡)状态下的合成器效率分析-理论与ADS仿真
- 1、隔离功率合成器(威尔金森功分器)
- 1.1、威尔金森功分器基本结构
- 1.2、威尔金森功分器的S参数仿真
- 1.3、威尔金森功分器在异相情况下的效率推导
- 1.4、威尔金森功分器在异相情况下的效率仿真
- 2、非隔离功率合成器(T功分器)
- 2.1、T功分器基本结构
- 2.2、T功分器的S参数
- 2.3、T功分器在异相情况下的效率推导
- 2.4、T功分器在异相情况下的效率仿真
1、隔离功率合成器(威尔金森功分器)
1.1、威尔金森功分器基本结构
隔离的功率合成器也就是威尔金森功分器,其基础的理论结构如下:

其对应的基本参数可由下式计算:

1.2、威尔金森功分器的S参数仿真
(Combine_EffiCompare原理图)
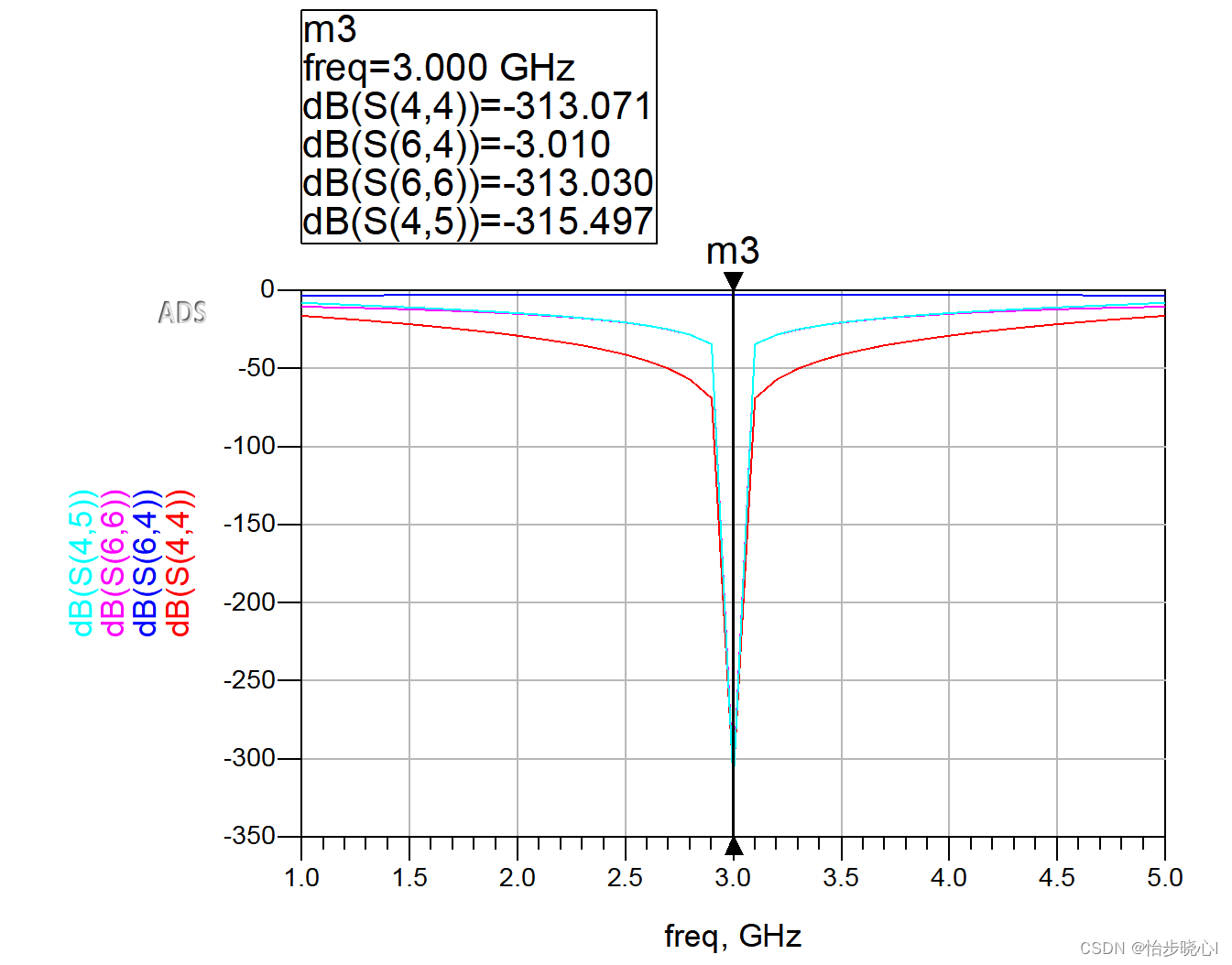
此处以3GHz的等分类型为例,此时k=1,构建如下原理图:
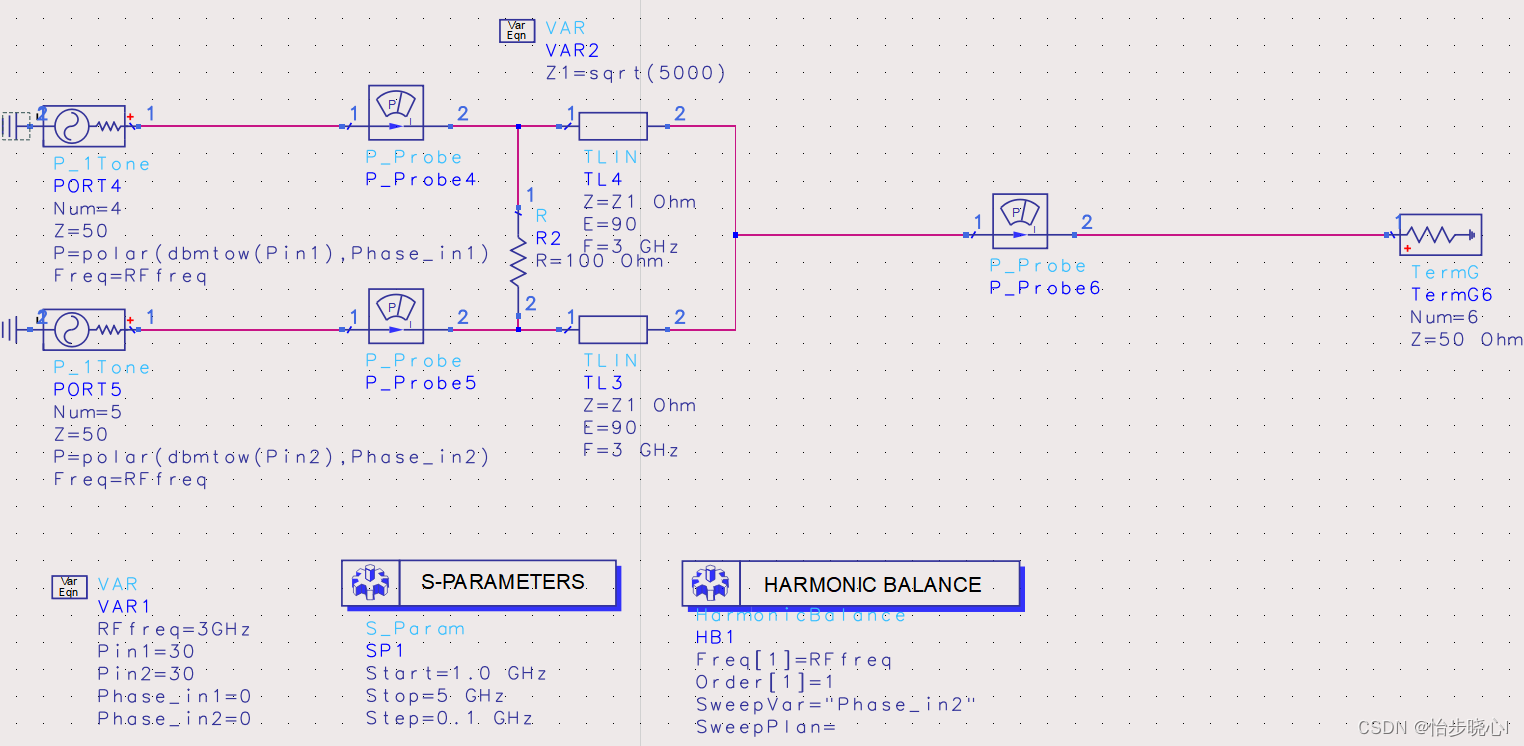
其理想结果如下所示,可以看到各个端口的回波损耗(S44、S66)都非常好,两端口的隔离S45非常理想,等分比是1:1,因此S64是3dB:
1.3、威尔金森功分器在异相情况下的效率推导
等分威尔金森功分器的输出端接在上下两支路接输入,实现具有隔离功能的功率合成,其框图如下:

假设经过信号分离出两路异相信号分别为(也就是输入信号):
s
1
(
t
)
=
A
2
cos
[
ω
t
+
φ
+
θ
]
s_{1}\left(t\right)=\frac{\mathrm{A}}{2}\cos\left[\omega t+\varphi+\theta\right]
s1(t)=2Acos[ωt+φ+θ]
s
2
(
t
)
=
A
2
cos
[
ω
t
+
φ
−
θ
]
s_{2}\left(t\right)=\frac{\mathrm{A}}{2}\cos\left[\omega t+\varphi-\theta\right]
s2(t)=2Acos[ωt+φ−θ]
若两路信号完全一致,那么隔离电阻上将无电流流经,从而使得等分威尔金森功率合成器无损耗地运行。然而,一旦输入端口1和端口2的信号存在相位不平衡,信号的同相部分将在输出端口3叠加,而反向部分则会通过隔离电阻,在两端产生电势差,进而形成电流流过隔离电阻,导致能量损失的产生。信号中的同相部分经功率合成后,从端口3输出的信号功率为:
P
o
u
t
=
∣
s
1
+
s
2
∣
2
=
A
2
2
cos
2
θ
P_{out}=\left|s_1+s_2\right|^2=\frac{A^2}{2}\cos^2\theta
Pout=∣s1+s2∣2=2A2cos2θ
信号反向部分经过隔离电阻损耗的功率为:
P
d
i
s
=
∣
s
1
−
s
2
∣
2
=
A
2
2
sin
2
θ
P_{dis}=\begin{vmatrix}s_1-s_2\end{vmatrix}^2=\frac{A^2}{2}\sin^2\theta
Pdis=
s1−s2
2=2A2sin2θ
等分威尔金森功率合成器合成异相信号的效率为:
η
1
=
P
o
u
t
P
d
i
s
+
P
o
u
t
=
cos
2
θ
\eta_1=\frac{P_{out}}{P_{dis}+P_{out}}=\cos^2\theta
η1=Pdis+PoutPout=cos2θ
1.4、威尔金森功分器在异相情况下的效率仿真
(Combine_EffiCompare原理图)
原理图中使用了Probe进行了功率测量:

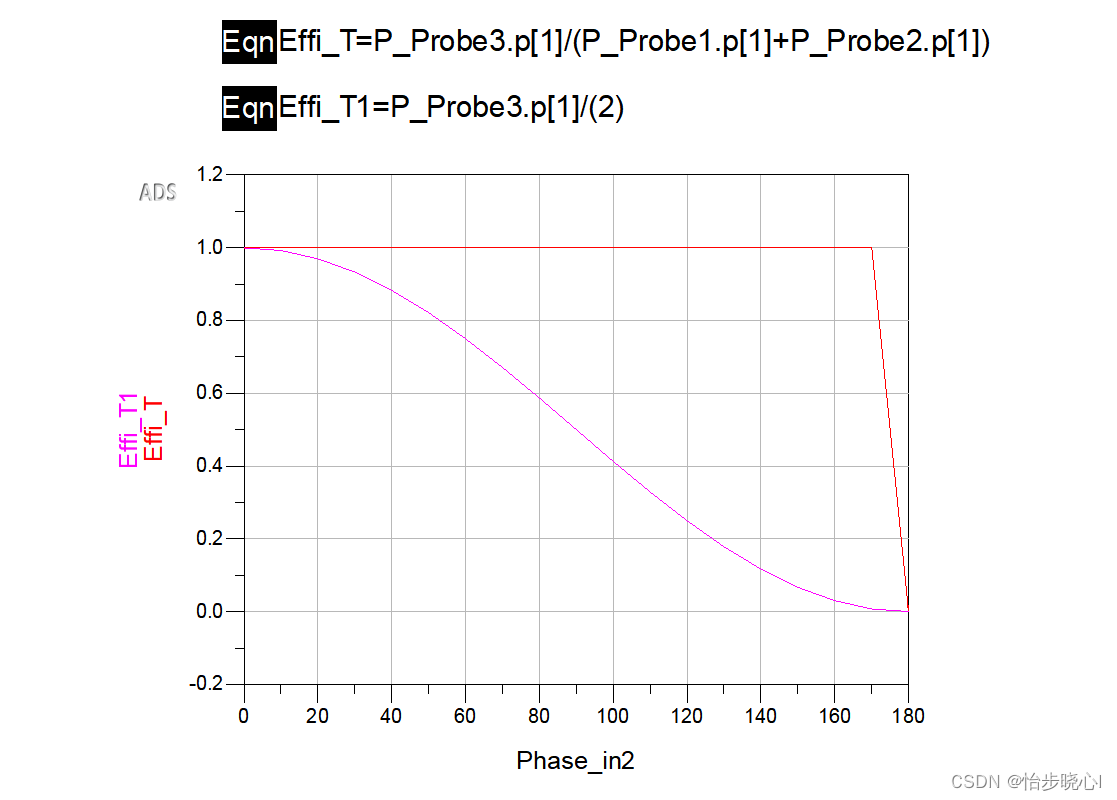
使用了Sweep查看不同异相角下的效率性能,结果和理论一致的:

需要注意的是,异相角为
θ
\theta
θ,代表第一路输入相对于参考信号的角度为
θ
\theta
θ,第二路输入相对于参考信号的角度为
−
θ
-\theta
−θ,实际上两路输入的相位差为
2
θ
2\theta
2θ。
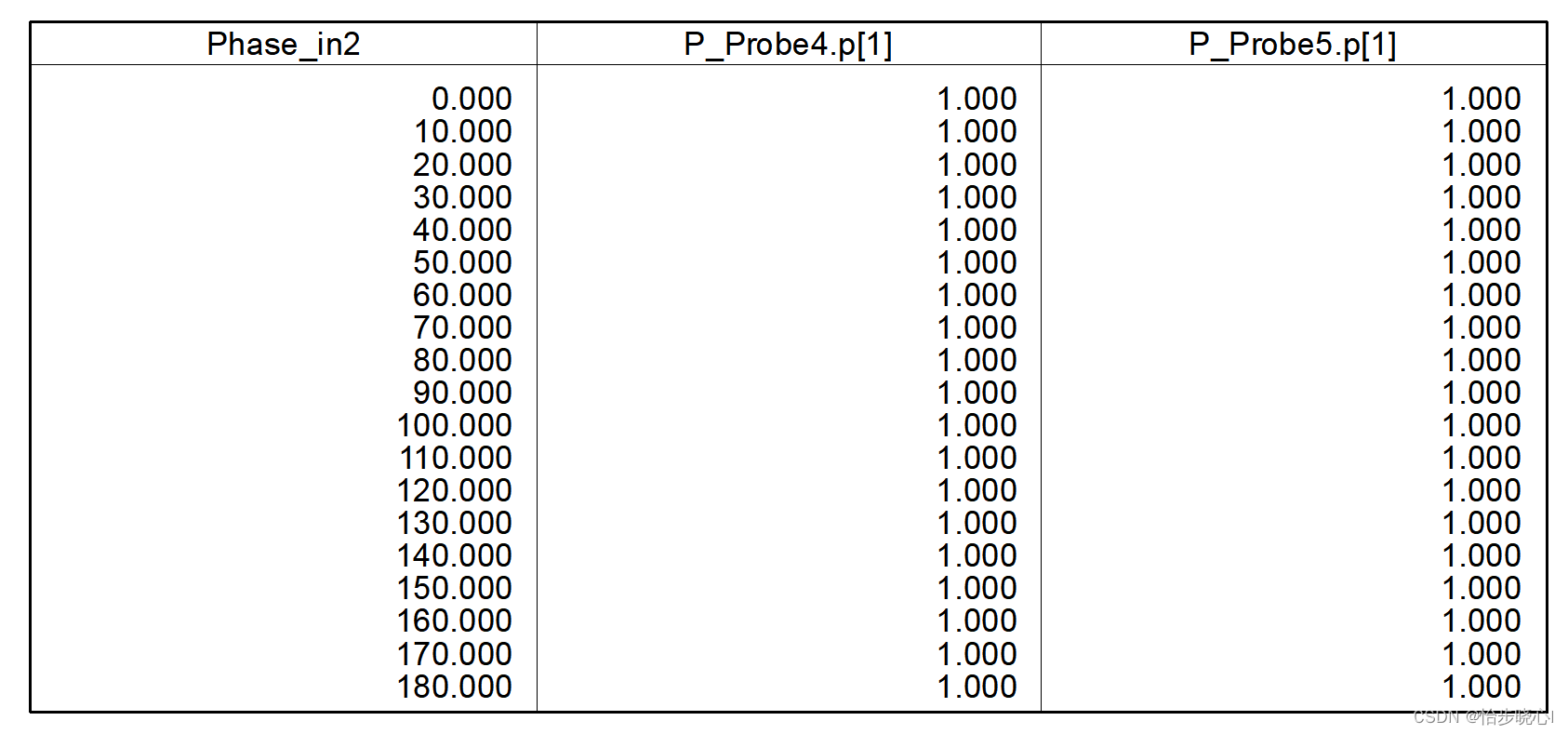
威尔金森功分器在异相情况下的净输入功率
非常重要的一点,仿真发现即使是异相状态,净输入功率也是恒定的1W(这个1W是自己设置的),这代表所有的功率都进入到了合路器,所有的损耗都是由隔离电阻导致的:
2、非隔离功率合成器(T功分器)
2.1、T功分器基本结构
这个T功分器的基本理论可以参考:01、T型结功分器
其基本结构是这样的:
(Combine_EffiCompare原理图)
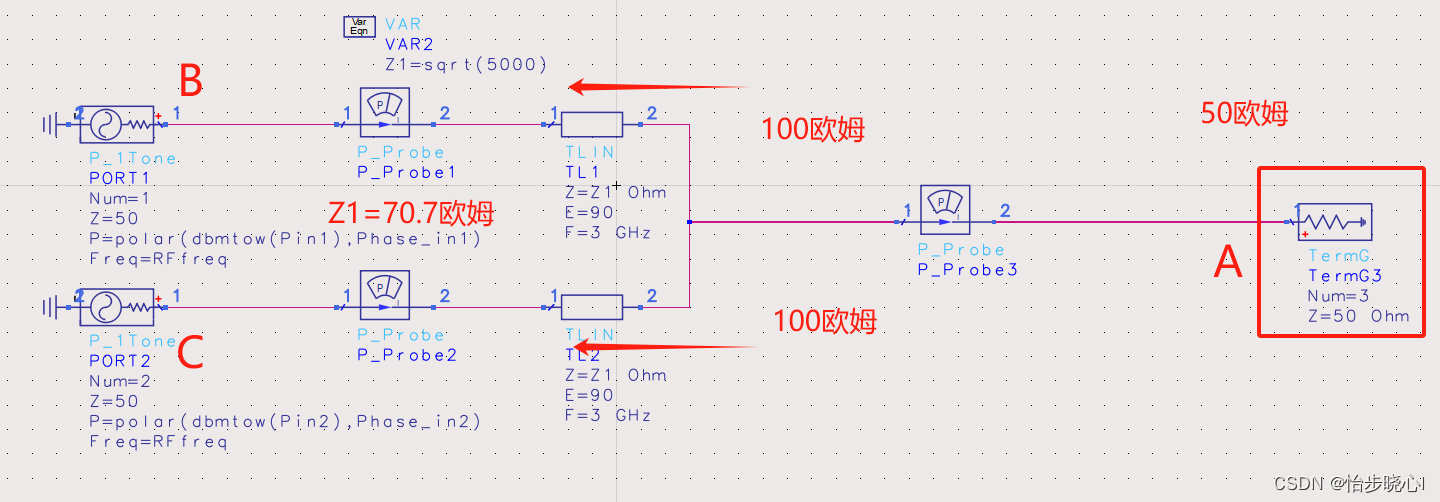
其优缺点可以参考:微波射频学习笔记10——–T型结功率分配器
T型优缺点
①B、C口不能作为输入,反过来看,阻抗就不是50Ω,不能全端口阻抗匹配;
②B、C两端口没有隔离开来,信号会相互影响到;
③优点暂时没想到,可能就是便宜,简单吧。
2.2、T功分器的S参数
(Combine_EffiCompare原理图)
对于上面的ADS原理图,其理想结果如下所示,可以看到3端口的回波损耗(S33)都非常好,两端口的隔离S21不太理想,等分比是1:1,因此S31是3dB。用作合路器时,其输入的回波损耗S11和S22都只有-6dB:

2.3、T功分器在异相情况下的效率推导
推导部分参考的是”基于高效率功率放大器的数字Outphasing 发射机研究与设计“的第四章,但是原作者的推导有误,式(4-16) 、式(4-17)、式(4-18)几个公式的效率算错了。
为了分析非隔离功率合成器的合成效率,其等效电路示意图如下:

两路射频电压信号源输出的电压信号设为:
V
1
=
G
S
1
′
(
t
)
=
G
A
2
e
j
φ
(
t
)
e
j
θ
(
t
)
=
V
0
e
j
θ
(
t
)
V
2
=
G
S
2
′
(
t
)
=
G
A
2
e
j
φ
(
t
)
e
−
j
θ
(
t
)
=
V
0
e
−
j
θ
V_1=GS_1'\left(t\right)=G\frac{A}{2}e^{j\varphi(t)}e^{j\theta(t)}=V_0e^{j\theta(t)}\\ \quad\\ V_{2}=GS_{2}^{'}\left(t\right)=G\frac{A}{2}e^{j\varphi(t)}e^{-j\theta(t)}=V_{0}e^{-j\theta}
V1=GS1′(t)=G2Aejφ(t)ejθ(t)=V0ejθ(t)V2=GS2′(t)=G2Aejφ(t)e−jθ(t)=V0e−jθ
射频电压源后接串联的四分之一波长传输线的构成的功率合成器,四分之一波长传输线的ABCD矩阵可以表示为:
T
=
[
cos
α
j
Z
0
sin
α
j
sin
α
Z
0
cos
α
]
=
[
0
j
Z
0
j
Z
0
0
]
T=\begin{bmatrix}\cos\alpha&jZ_0\sin\alpha\\\frac{j\sin\alpha}{Z_0}&\cos\alpha\end{bmatrix}=\begin{bmatrix}0&jZ_0\\[0.3em]\frac{j}{Z_0}&0\end{bmatrix}
T=[cosαZ0jsinαjZ0sinαcosα]=[0Z0jjZ00]
其中
α
\alpha
α为传输线的电长度,四分之一波长对应的电长度为90度。Z0为微带线特性阻抗。根据四分之一波长传输线输入输出与ABCD参数的关系,上下两条支路电压电流关系可以表示为:
[
V
1
I
1
]
=
T
⋅
[
V
L
I
11
]
[
V
2
I
2
]
=
T
⋅
[
V
L
I
22
]
\begin{bmatrix}V_1\\I_1\end{bmatrix}=T\cdot\begin{bmatrix}V_L\\I_{11}\end{bmatrix}\\ \quad\\ \begin{bmatrix}V_2\\I_2\end{bmatrix}=T\cdot\begin{bmatrix}V_L\\I_{22}\end{bmatrix}
[V1I1]=T⋅[VLI11][V2I2]=T⋅[VLI22]
其中VL为输出端电压,
I
11
、
I
22
I_{_{11}}、I_{_{22}}
I11、I22分别为两支路四分之一波长线的输出电流,综合上式可得:
I
L
=
I
11
+
I
22
=
V
0
(
e
j
θ
+
e
−
j
θ
)
j
Z
0
=
2
V
0
cos
θ
j
Z
0
V
L
=
2
V
0
cos
θ
j
Z
0
R
L
=
G
R
L
Z
0
[
e
j
φ
(
t
)
A
cos
θ
]
e
−
j
π
2
=
G
R
L
Z
0
S
(
t
)
e
−
j
π
2
I_L=I_{11}+I_{22}=\frac{V_0\left(e^{j\theta}+e^{-j\theta}\right)}{jZ_0}=\frac{2V_0\cos\theta}{jZ_0}\\ \quad\\ V_{L}=\frac{2V_{0}\cos\theta}{jZ_{0}}R_{L}=\frac{GR_{L}}{Z_{0}}\biggl[e^{j\varphi(t)}A\cos\theta\biggr]e^{-j\frac{\pi}{2}}=\frac{GR_{L}}{Z_{0}}S\bigl(t\bigr)e^{-j\frac{\pi}{2}}
IL=I11+I22=jZ0V0(ejθ+e−jθ)=jZ02V0cosθVL=jZ02V0cosθRL=Z0GRL[ejφ(t)Acosθ]e−j2π=Z0GRLS(t)e−j2π
两支路输入电流有如下关系:
I
1
=
I
2
=
2
V
0
cos
θ
Z
0
2
R
L
I_1=I_2=\frac{2V_0\cos\theta}{\frac{Z_0^2}{R_L}}
I1=I2=RLZ022V0cosθ
上支路放大信号输入到功率合成器的信号功率可以表示为:
P
1
=
1
2
Re
(
V
1
⋅
I
1
∗
)
=
1
2
Re
(
V
0
e
j
θ
⋅
2
V
0
∗
cos
θ
Z
0
2
R
L
)
=
A
2
cos
2
θ
Z
0
2
R
L
P_1=\frac{1}{2}\operatorname{Re}\left(V_1\cdot I_1^*\right)=\frac{1}{2}\operatorname{Re}\left(V_0e^{j\theta}\cdot\frac{2V_0^*\cos\theta}{\frac{Z_0^2}{R_L}}\right)=\frac{A^2\cos^2\theta}{\frac{Z_0^2}{R_L}}
P1=21Re(V1⋅I1∗)=21Re
V0ejθ⋅RLZ022V0∗cosθ
=RLZ02A2cos2θ
下支路放大信号输入到功率合成器的信号功率为:
P
2
=
1
2
Re
(
V
2
⋅
I
2
∗
)
=
1
2
Re
(
V
0
e
−
j
θ
⋅
2
V
0
∗
cos
θ
Z
0
2
R
L
)
=
A
2
cos
2
θ
Z
0
2
R
L
P_2=\frac{1}{2}\operatorname{Re}\Big(V_2\cdot I_2^*\Big)=\frac{1}{2}\operatorname{Re}\Bigg(V_0e^{-j\theta}\cdot\frac{2V_0^*\cos\theta}{\frac{Z_0^2}{R_L}}\Bigg)=\frac{A^2\cos^2\theta}{\frac{Z_0^2}{R_L}}
P2=21Re(V2⋅I2∗)=21Re(V0e−jθ⋅RLZ022V0∗cosθ)=RLZ02A2cos2θ
输入到功率合成器的总功率为:
P
=
P
1
+
P
2
=
2
A
2
cos
θ
Z
0
2
R
L
P=P_1+P_2=\frac{2A^2\cos\theta}{\frac{Z_0^2}{R_L}}
P=P1+P2=RLZ022A2cosθ
功率合成器输出的功率为:
P
o
u
t
=
1
2
Re
(
V
L
⋅
I
L
∗
)
=
1
2
Re
(
2
V
0
cos
θ
j
Z
0
R
L
⋅
2
V
0
∗
cos
θ
j
Z
0
)
=
2
A
2
cos
2
θ
Z
0
2
R
L
P_{\mathrm{out}}=\frac{1}{2}\operatorname{Re}\Big(V_{L}\cdot I_{L}^{*}\Big)=\frac{1}{2}\operatorname{Re}\Bigg(\frac{2V_{0}\cos\theta}{jZ_{0}}R_{L}\cdot\frac{2V_{0}^{*}\cos\theta}{jZ_{0}}\Bigg)=\frac{2A^{2}\cos^{2}\theta}{\frac{Z_{0}^{2}}{R_{L}}}
Pout=21Re(VL⋅IL∗)=21Re(jZ02V0cosθRL⋅jZ02V0∗cosθ)=RLZ022A2cos2θ
所以非隔离功率合成器合成异相信号的合成效率为:
η
2
=
P
o
u
t
P
=
1
\eta_2=\frac{P_{out}}{P}=1
η2=PPout=1
可以看到,如果按照正确的推导方式,异相情况下的T型功分器效率为100%。
然而,虽然看起来非常的美好,但是此处的推导时争对于输入到合路器的效率。但是,假设的源的输出功率是1W,但是实际在异相状态下输入到合路器的功率就不是1W了,从下面仿真可以看出。
2.4、T功分器在异相情况下的效率仿真
(Combine_EffiCompare原理图)
可以看到,如果使用Probe进行功率测量,得到的理论效率结果为100%,这也非常正常,因为电路没有有耗器件:
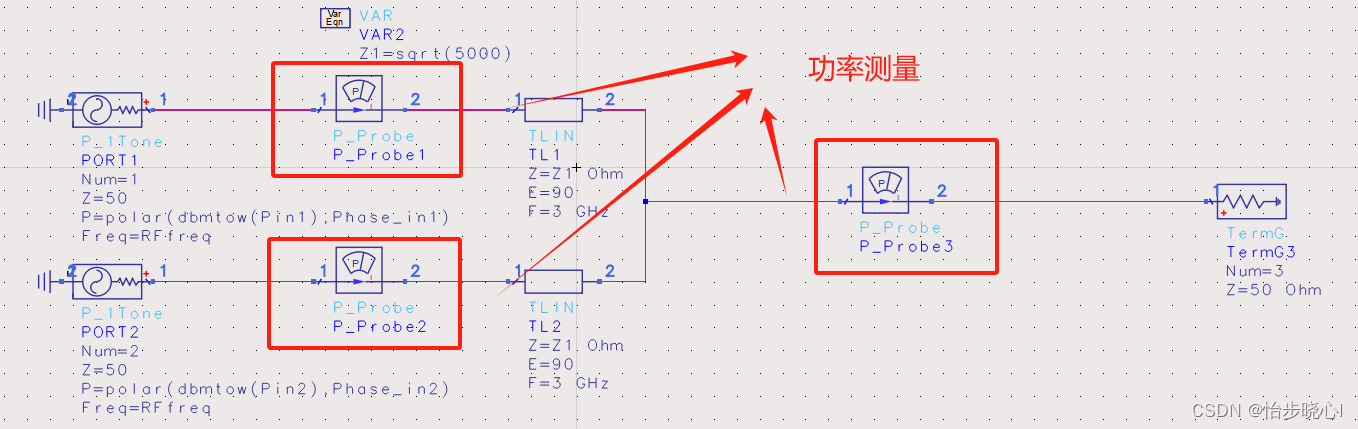

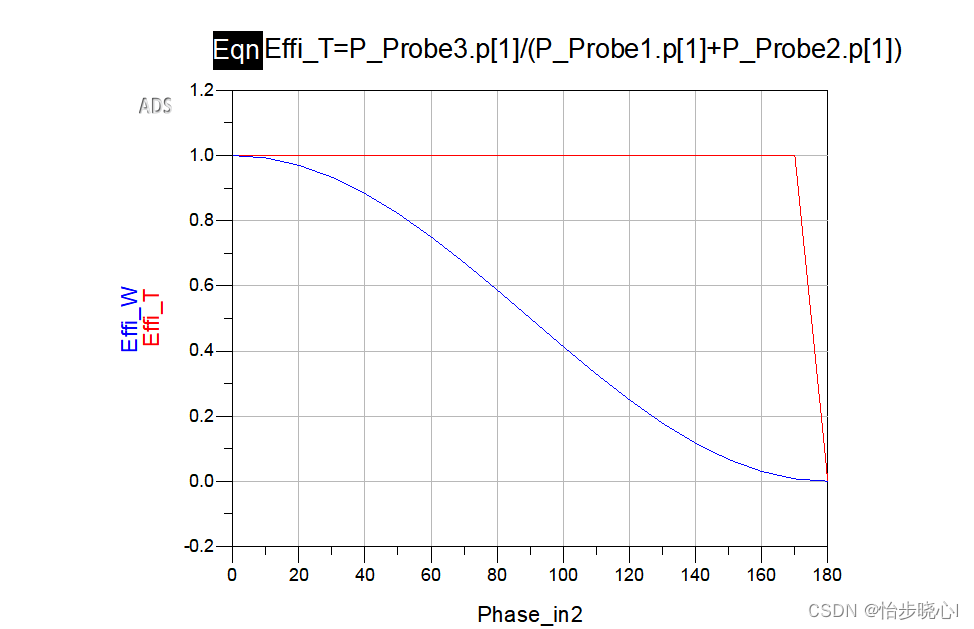
但是,虽然端口的输入功率设置为1W,其净输入功率并非1W,这可能是由于端口的匹配和隔离性能不佳:
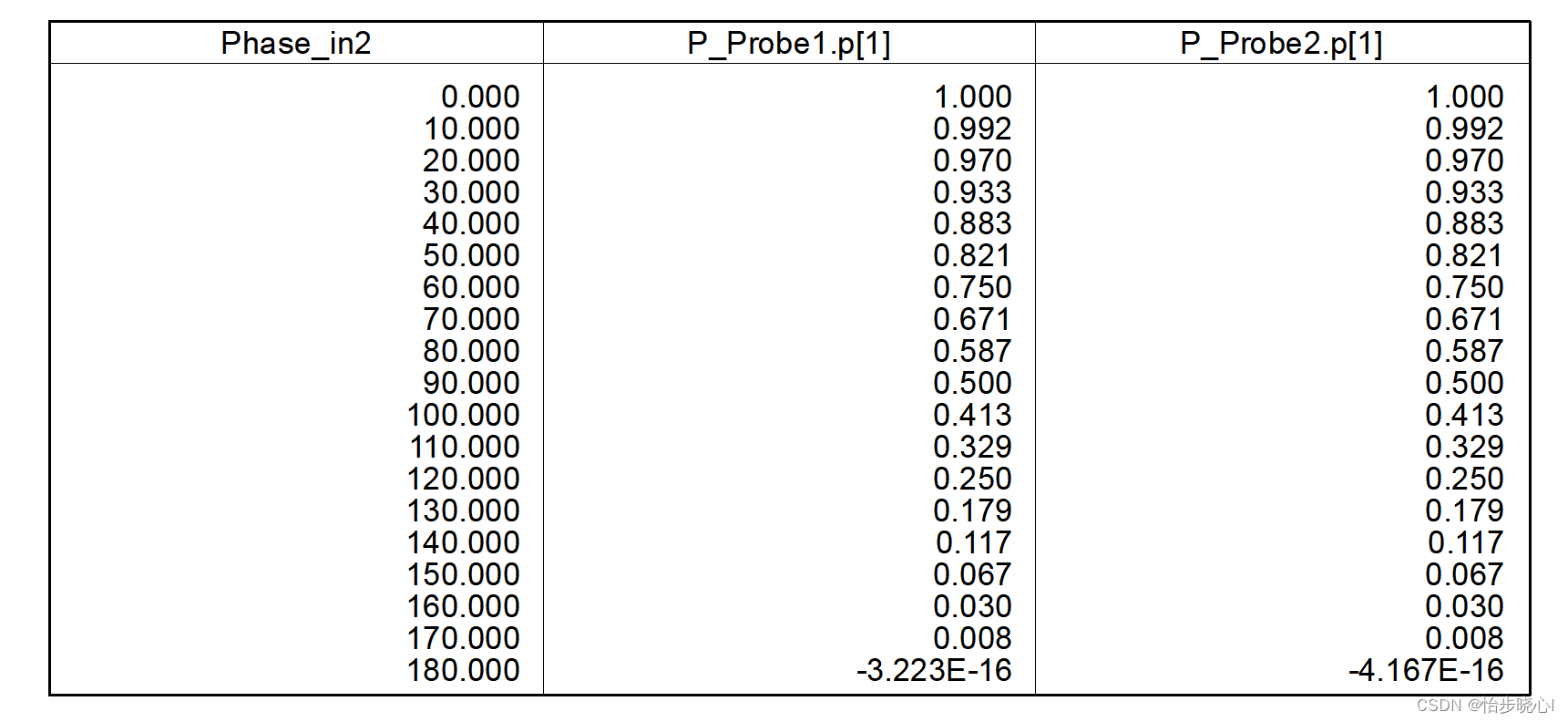
因此,如果按照输入功率来计算效率,而不是按照净输入功率来计算效率,其实际的效率和威尔金森功分器是一致的: