超简单白话文机器学习 - 回归树树剪枝（含算法介绍，公式，源代码实现以及调包实现）

1. 回归树

1.1 算法介绍

大家看到这篇文章时想必已经对树这个概念已经有基础了，如果不是很了解的朋友可以看看笔者的这篇文章：

超简单白话文机器学习-决策树算法全解（含算法介绍，公式，源代码实现以及调包实现）_白话决策树-CSDN博客

对于回归树的建立，我们一般使用CART回归树，CART(Classification and Regression Trees)回归树是一种用于连续值预测的树模型。它通过递归地分裂数据集，以最小化预测误差为目标，最终生成一棵树结构的模型。

CART回归树的构建核心是选择最佳分裂点通过计算MSE进行衡量。

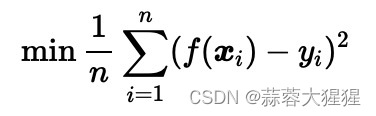
1. 选择最佳分裂点，对每个特征尝试所有的分裂点，计算分裂后各个数据集的均方误差。

2. 计算分裂前后的总MSE：

其中，n为总样本数，各分子分别是左子节点和右子节点的样本数。

3. 递归分裂，对每个子节点重复上述步骤直到满足停止条件（例如达到最大深度或叶节点中的样本数少于阈值）

获得最佳划分特征之后，需要确定分裂节点的阈值，需要最小化目标函数

1. 首先对于最佳划分特征中的数值进行迭代。

2. 对于该特征特定数值进行分裂的样本进行错误率的计算。

3. 汇总后选择错误率最小的数值作为阈值选择。

2. 树剪枝概述

2.1 预剪枝

2.1.1 算法

预剪枝的核心是在生成决策树的过程中提前停止树的增长。计算当前的划分是否能带来模型泛化能力的提升，如果不能，则不再继续生长子树。

有如下几种方法：

( 1 ）当树到达一定深度的时候，停止树的生长。
( 2 ）当到达当前结点的样本数量小于某个阈值的时候，停止树的生长。
( 3 ）计算每次分裂对测试集的准确度提升，当小于某个阈值的时候，不再继续扩展。

2.2 后剪枝

2.2.1 算法

首先我们先讲后剪枝的伪代码用口水话进行呈现：

基于已有的树切分测试数据：

1. 如果存在任一子集是一棵树，则在该子集递归剪枝过程

2. 计算将当前两个叶节点合并后的误差

3. 计算不合并的误差

4. 如果合并可以降低误差，就合并

剪枝策略：

如果剪枝后的叶节点误差小于或等于未剪枝子树的误差，则进行剪枝，即将该内部节点变为叶节点。继续评估和剪枝树中的其他节点，直到不再有可以进一步剪枝的节点。

误差的衡量方式有多种，回归树的误差衡量我们一般选择MSE。

2.2.2 代价复杂度剪枝

前文我们已经讲了，防止过拟合的方法之一时，对决策树进行剪枝，即减少树的分支。 剪枝防止过拟合使得在测试集上的表现更好。

将公式呈现在这里：

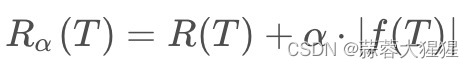
让我们用白话文转化一下这个公式：

评价一棵树的得分由两部分组成，第一部分为SSR，一种预测错误率的衡量方式。第二部分代表决策树T的叶子结点个数，阿尔法是自定义指数，需要通过交叉验证的方式得到最佳参数，不同的参数影响最终所生成的树。

举个例子：

对于这四个树我们取得了他们总体的SSR值，假设我们的参数值为1000，计算树的得分。

选取得分最小的树作为我们的预测模型，即第一棵树拥有四个叶子节点。改变参数值会选择不同的预测模型，让我们计算在什么参数值下会分别指向哪一棵树。

在不同参数值的条件下，我们使用测试集迭代进行交叉验证，根据测试集最后的得分我们选择最佳参数作为判断标准，最终构造我们的预测树模型。

3. 手写代码实现

3.1 回归树

def regLeaf(dataset):
    return np.mean(dataset[:,-1]) #得到叶结点，目标变量的均值
    
def regErr(dataset):
    return np.var(dataset[:,-1]) * np.shape(dataset)[0] #返回的是总方差

def chooseBestSplit(dataset,leafType=regLeaf,errType=regErr,ops=(1,4)):
    tols = ops[0];tolN = ops[1] #tols是容许的误差下降值, yolN是切分的最少样本数
    if len(set(dataset[:,-1].T.tolist()[0])) == 1: #如果剩余特征为1
        return None,leafType(dataset) #直接返回叶子结点
    m,n = np.shape(dataset)
    S = errType(dataset) #数据集的总误差
    bestS = 100000; bestIndex=0;bestvalue = 0
    for featIndex in range(n-1):
        for splitVal in set(dataset[:,featIndex]): #对于某特征不同值的集合进行迭代
            mat0,mat1 = binSplitDataset(dataset,feat,splitVal)
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue #如果不满足最少切分样本树
            newS = errType(mat0) + errorType(mat1) #返回数据集的总方差
            if newS < bestS: #选择总方差最少的数据分类方式
                bestIndex = feat
                bestvalue = splitVal
                bestS = newS
    if (S - bestS) < tols: #如果小于要求的误差下降值，则直接返回叶子结点
        return None,leafType(dataset)
    mat0,mat1 = binSplitDataset(dataset,bestIndex,bestvalue)
    if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
        return None, leafType(dataset)
    return bestIndex,bestValue

4. 调包实现

4.1 预剪枝

import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据集
data = load_iris()
X = data.data
y = data.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 设置预剪枝条件
max_depth = 3  # 限制树的最大深度
min_samples_split = 4  # 分裂一个内部节点所需的最小样本数
min_samples_leaf = 2  # 叶节点所需的最小样本数

# 初始化并训练决策树分类器
clf = DecisionTreeClassifier(random_state=42, 
                             max_depth=max_depth, 
                             min_samples_split=min_samples_split, 
                             min_samples_leaf=min_samples_leaf)

clf.fit(X_train, y_train)

# 预测并评估模型性能
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)

print(f'预剪枝条件下的决策树分类器准确率: {accuracy:.4f}')

# 可视化决策树（需要graphviz支持）
from sklearn.tree import export_graphviz
import graphviz

dot_data = export_graphviz(clf, out_file=None, 
                           feature_names=data.feature_names,  
                           class_names=data.target_names,  
                           filled=True, rounded=True,  
                           special_characters=True)  
graph = graphviz.Source(dot_data)  
graph.render("iris_prepruned_tree")  # 将树保存为PDF文件
graph  # 在Jupyter Notebook中显示决策树

4.2 后剪枝

import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split, cross_val_score
import matplotlib.pyplot as plt

# 示例数据集
X = np.array([[2.7, 2.5], [1.3, 1.5], [3.2, 2.8], [3.8, 2.5], [2.9, 2.4],
              [6.5, 3.1], [7.1, 3.4], [6.0, 2.9], [7.6, 3.2], [6.3, 3.0]])
y = np.array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 生成完整的决策树
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)

# 获取剪枝路径
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

# 遍历不同的剪枝参数，选择最佳剪枝
clfs = []
for ccp_alpha in ccp_alphas:
    clf = DecisionTreeClassifier(random_state=42, ccp_alpha=ccp_alpha)
    clf.fit(X_train, y_train)
    clfs.append(clf)

# 交叉验证选择最佳剪枝参数
alpha_scores = [cross_val_score(clf, X_train, y_train, cv=2).mean() for clf in clfs]
best_clf = clfs[np.argmax(alpha_scores)]

# 在测试集上评估最佳模型
test_score = best_clf.score(X_test, y_test)
print(f'Best alpha: {ccp_alphas[np.argmax(alpha_scores)]}')
print(f'Test set score: {test_score}')

# 可视化剪枝路径
plt.figure(figsize=(10, 6))
plt.plot(ccp_alphas, alpha_scores, marker='o', drawstyle='steps-post')
plt.xlabel('Alpha')
plt.ylabel('Cross-validated accuracy')
plt.title('Alpha vs Cross-validated accuracy')
plt.show()