Redis 源码学习记录：集合 (set)

无序集合

Redis 源码版本：Redis-6.0.9，本篇文章无序集合的代码均在 intset.h / intset.c 文件中。

Redis 通常使用字典结构保存用户集合数据，字典键存储集合元素，字典值为空。如果一个集合全是整数，则使用字典国语浪费内存。为此，Redis 设计了 intset 数据结构，专门用来保存整数集合数据。

定义

typedef struct intset {
    uint32_t encoding; // 编码格式，intset 中所有元素必须是同一种编码格式
    uint32_t length;   // 集合中元素的数量
    int8_t contents[]; // 存储元素数据，元素必须排序，并且无重复
} intset;

encoding 格式如下表所示：

定义	存储类型
`INTSET_ENC_INT16`	`int16_t`
`INTSET_ENC_INT32`	`int32_t`
`INTSET_ENC_INT64`	`int64_t`

intset 编码格式存在不同的级别。上表中编码格式的级别由低到高排序：

$\rm INTSET\_ENC\_INT16 \lt INTSET\_ENC\_INT32 \lt INTSET\_ENC\_INT64$

`intsetAdd`

函数功能：向 intset 中插入一个元素。
参数：
- intset *is：插入到指定的 intset 中。
- int64_t value：插入指定的元素。
- uint8_t *success：是否插入成功。
返回值：返回该 intset，因为在该函数中可能会修改原 intset 的地址。

intset *intsetAdd(intset *is, int64_t value, uint8_t *success) {
    uint8_t valenc = _intsetValueEncoding(value); // 判断 val 值对应的 intset 编码
    uint32_t pos;
    if (success) *success = 1; // 如果 success != NULL 默认 Add 成功

    /* Upgrade encoding if necessary. If we need to upgrade, we know that
     * this value should be either appended (if > 0) or prepended (if < 0),
     * because it lies outside the range of existing values. */
    
    // 如果参数 value 对应的编码大于 intset 中元素的编码。 intrev32ifbe 函数用于转换字节序
    if (valenc > intrev32ifbe(is->encoding)) { 
        /* This always succeeds, so we don't need to curry *success. */
        return intsetUpgradeAndAdd(is,value); // 升级 intset 的编码，然后插入数据
    } else {
        /* Abort if the value is already present in the set.
         * This call will populate "pos" with the right position to insert
         * the value when it cannot be found. */
        if (intsetSearch(is,value,&pos)) { // 如果 intset 中已经存在与 value 相同的值
            if (success) *success = 0; // 那么插入失败
            return is;
        }
		// 走到这里说明 intset 中不存在与 value 相同的值，并且不用调整原 intset 的编码
        is = intsetResize(is,intrev32ifbe(is->length)+1); // 只需要调整 intset 的大小就行啦
        // 这个 if 判断几乎不可能判断失败的，但是为什么这么做，懂得都懂
        if (pos < intrev32ifbe(is->length)) intsetMoveTail(is,pos,pos+1); // 将原 intset pos 位置及其之后的元素全部后移一个下标
    }

    _intsetSet(is,pos,value); // 将 value 插入到 pos 位置处
    is->length = intrev32ifbe(intrev32ifbe(is->length)+1); // 更新 intset 的 length 属性
    return is;
}

`_intsetValueEncoding`

函数功能：根据整数的大小判断其在 intset 中的编码。
参数：
- int64_t v)：待判断编码的整数。
返回值：该整数的编码。

#define INTSET_ENC_INT16 (sizeof(int16_t))
#define INTSET_ENC_INT32 (sizeof(int32_t))
#define INTSET_ENC_INT64 (sizeof(int64_t))

static uint8_t _intsetValueEncoding(int64_t v) {
    if (v < INT32_MIN || v > INT32_MAX)
        return INTSET_ENC_INT64;
    else if (v < INT16_MIN || v > INT16_MAX)
        return INTSET_ENC_INT32;
    else
        return INTSET_ENC_INT16;
}

`intsetUpgradeAndAdd`

函数功能：升级 intset 的编码格式，并将指定的 value 值插入到 intset。
参数：
- intset *is：需要升级编码和插入元素的 intset。
- int64_t value：待插入的 value。
返回值：升级之后的 intset。

/* Upgrades the intset to a larger encoding and inserts the given integer. */
static intset *intsetUpgradeAndAdd(intset *is, int64_t value) {
    uint8_t curenc = intrev32ifbe(is->encoding); // 当前 intset 的编码格式
    uint8_t newenc = _intsetValueEncoding(value); // 升级之后 intset 的编码格式
    int length = intrev32ifbe(is->length); // 当前 intset 中元素的个数
    int prepend = value < 0 ? 1 : 0; // 判断下标的偏移

    /* First set new encoding and resize */
    is->encoding = intrev32ifbe(newenc); // 修改 intset 的编码
    is = intsetResize(is,intrev32ifbe(is->length)+1); // 调整 intset 的大小，+1 是因为等会儿要插入一个新元素嘛

    
    // _intsetGetEncoded(is,length,curenc) 将原来的 intset 的数据获取出来，从后向前获取的哇
    // _intsetSet 将 _intsetGetEncoded 直接插入到新的 intset 中，从后向前插入
    // length+prepend 如果 value 小于 0  prepend 就是 1，因为负数是插入到柔性数组下标为 0 的位置，下标在数值上就会向后偏移一个。
    // 如果 value >= 0 prepend 就是 0 直接插入到柔性数组末尾就行了，下标在数值上就不会偏移了
    while(length--)
        _intsetSet(is,length+prepend,_intsetGetEncoded(is,length,curenc));

    /* Set the value at the beginning or the end. */
    // [1](见注解1)
    if (prepend)
        _intsetSet(is,0,value); // 如果 value < 0 将新插入的值设置到柔性数组下标为 0 的位置
    else
        _intsetSet(is,intrev32ifbe(is->length),value); // 如果 value >= 0 将新插入的值设置到柔性数组末尾哈
    is->length = intrev32ifbe(intrev32ifbe(is->length)+1); // 更新 intset 的 length 属性 (集合中元素的个数)
    return is;
}

intset 虽说是用来实现无序集合的，但是其内部数据在柔性数组中的排列其实是有序的！下面我们来看看 intset 内部数据有序的必要性：
- 提升查找效率：有序数组允许使用二分查找算法，而二分查找的时间复杂度是 $\rm O(log⁡n)$ 。相比于无序数组的线性查找 $\rm O(n)$ ，二分查找能够显著提升查找操作的性能。当集合中的元素数量增加时，这种性能差异尤其明显。
- 简化重复元素检测：在插入新元素时，有序数组可以通过二分查找快速确定元素是否已经存在于集合中。如果元素已经存在，则直接返回，避免重复插入。这样的实现方式比起无序数组需要遍历整个数组来检查重复元素更加高效。
- 优化内存管理：有序数组在进行插入和删除操作时，可以通过简单的内存移动来保持数组的有序性，而不需要像哈希表那样复杂的重哈希和冲突解决机制。对于小型整数集合，intset 的内存占用也更为紧凑和高效。
- 简化编码和实现：有序数组的实现相对简单，操作逻辑容易理解和维护。保持有序性可以使许多操作在实现上更加直观，比如插入和查找操作。
无序集合的另一种实现方式就是使用 dict 这种实现方式下自然就不能保证数据的有序性啦！

回到插入数据的这条语句：使用该函数插入数据，已经明确了插入的数据超出了原 intset 编码的数值范围，其在原 intset 中要么是最大值，要么是最小值。因此，只需要判断这个数的正负选择是尾插还是头插就行了！这样就保证了 intset 内部数据的有序性啦！

`intsetResize`

函数功能：调整 intset 的大小。
参数：
- intset *is：需要调整大小的 intset。
- uint32_t len：intset 中元素的个数。
返回值：调整大小之后的 intset。

/* Resize the intset */
static intset *intsetResize(intset *is, uint32_t len) {
    uint32_t size = len*intrev32ifbe(is->encoding); //　新的柔性数组的大小
    is = zrealloc(is,sizeof(intset)+size);　// intset 扩容
    return is;
}

`_intsetSet`

函数功能：将一个 value 值设置到 intset 的指定位置。
参数：
- intset *is：设置 value 的 intset。
- int pos：设置 value 的位置。柔性数组的下标。
- int64_t value：待设置的值。
返回值：无。

/* Set the value at pos, using the configured encoding. */
static void _intsetSet(intset *is, int pos, int64_t value) {
    uint32_t encoding = intrev32ifbe(is->encoding);

    if (encoding == INTSET_ENC_INT64) {
        ((int64_t*)is->contents)[pos] = value; // 将值设置到指定的位置
        memrev64ifbe(((int64_t*)is->contents)+pos); // 转化字节序
    } else if (encoding == INTSET_ENC_INT32) {
        ((int32_t*)is->contents)[pos] = value;
        memrev32ifbe(((int32_t*)is->contents)+pos);
    } else {
        ((int16_t*)is->contents)[pos] = value;
        memrev16ifbe(((int16_t*)is->contents)+pos);
    }
}

`_intsetGetEncoded`

函数功能：根据指定的 encoding 编码获取指定位置下该编码的 value。
参数：
- intset *is：获取 value 的 intset 。
- int pos：指定 value 的起始位置。
- uint8_t enc：指定获取数据的编码。
返回值：获取到的 value 值。

/* Return the value at pos, given an encoding. */
static int64_t _intsetGetEncoded(intset *is, int pos, uint8_t enc) {
    int64_t v64;
    int32_t v32;
    int16_t v16;

    if (enc == INTSET_ENC_INT64) {
        memcpy(&v64,((int64_t*)is->contents)+pos,sizeof(v64)); // 获取值
        memrev64ifbe(&v64); // 转化字节序
        return v64; // 返回结果
    } else if (enc == INTSET_ENC_INT32) {
        memcpy(&v32,((int32_t*)is->contents)+pos,sizeof(v32));
        memrev32ifbe(&v32);
        return v32;
    } else {
        memcpy(&v16,((int16_t*)is->contents)+pos,sizeof(v16));
        memrev16ifbe(&v16);
        return v16;
    }
}

`intsetSearch`

函数功能：在 intset 中查找一个整数。
参数：
- intset *is：一个 intset。
- int64_t value：待查找的值。
- uint32_t *pos：当 pos != NULL 时：
  - 如果返回值为 1：表示 intset 中已经存在这个 value，*pos 为该值在 intset 中的下标。
  - 如果返回值为 0：表示 intset 中不存在这个 value，*pos 为其应该插入到 intset 中的下标。
返回值：intset 中是否已经存在相同的 value。
- 1：已经存在。
- 0：不存在。

/* Search for the position of "value". Return 1 when the value was found and
 * sets "pos" to the position of the value within the intset. Return 0 when
 * the value is not present in the intset and sets "pos" to the position
 * where "value" can be inserted. */
static uint8_t intsetSearch(intset *is, int64_t value, uint32_t *pos) {
    int min = 0, max = intrev32ifbe(is->length)-1, mid = -1;
    int64_t cur = -1;

    /* The value can never be found when the set is empty */
    if (intrev32ifbe(is->length) == 0) { // 如果当前的 intset 中没有元素
        if (pos) *pos = 0; // 如果 pos 不为 NULL 那么将 value 的下标保存到 *pos
        return 0;
    } else {
        /* Check for the case where we know we cannot find the value,
         * but do know the insert position. */
        // 比较 value 与柔性数组的两端元素的大小关系，尝试确定 value 的位置
        if (value > _intsetGet(is,max)) { // 如果比柔性数组中最大的元素还大，那么插入位置确定
            if (pos) *pos = intrev32ifbe(is->length); // 如果 pos 不为 NULL 那么将 value 的下标保存到 *pos
            return 0;
        } else if (value < _intsetGet(is,0)) { // 如果比柔性数组中最小的元素还小，那么插入位置确定
            if (pos) *pos = 0; // 如果 pos 不为 NULL 那么将 value 的下标保存到 *pos
            return 0;
        }
    }

    // 下面进行二分查找
    while(max >= min) {
        mid = ((unsigned int)min + (unsigned int)max) >> 1;
        cur = _intsetGet(is,mid); // 获取 mid 下标对应的值
        if (value > cur) { // 缩小查找的区间
            min = mid+1;
        } else if (value < cur) {
            max = mid-1;
        } else { // 找到了，直接退出循环
            break;
        }
    }

    if (value == cur) { // 如果找到了 value
        if (pos) *pos = mid; // 如果 pos 不为 NULL 那么将与 value 值相同元素的下标保存到 *pos
        return 1;
    } else { // 没有找到
        if (pos) *pos = min; // 如果 pos 不为 NULL 那么将 value 应在的下标保存到 *pos
        return 0;
    }
}

`_intsetGet`

函数功能：获取 intset 中指定下标的元素。
参数：
- intset *is：指定的 intset。
- int pos：指定的下标。
返回值：获取到的 value。

/* Return the value at pos, using the configured encoding. */
static int64_t _intsetGet(intset *is, int pos) {
    return _intsetGetEncoded(is,pos,intrev32ifbe(is->encoding));
}

`intsetMoveTail`

函数功能：将 intset 中指定下标及其之后的所有元素移动到指定位置处。
参数：
- intset *is：数据所在的 intset。
- uint32_t from：从 from 下标开始及其之后的所有元素均需要移动。
- uint32_t to：移动到 to 下标处。
返回值：

static void intsetMoveTail(intset *is, uint32_t from, uint32_t to) {
    void *src, *dst;
    uint32_t bytes = intrev32ifbe(is->length)-from; // 需要移动的元素个数
    uint32_t encoding = intrev32ifbe(is->encoding); // intset 的编码

    // 根据编码确定 memmove 函数的起始地址和目标地址，计算需要移动多少字节
    if (encoding == INTSET_ENC_INT64) {
        src = (int64_t*)is->contents+from;
        dst = (int64_t*)is->contents+to;
        bytes *= sizeof(int64_t);
    } else if (encoding == INTSET_ENC_INT32) {
        src = (int32_t*)is->contents+from;
        dst = (int32_t*)is->contents+to;
        bytes *= sizeof(int32_t);
    } else {
        src = (int16_t*)is->contents+from;
        dst = (int16_t*)is->contents+to;
        bytes *= sizeof(int16_t);
    }
    memmove(dst,src,bytes); // 移动元素
}

仅以 intsetAdd 函数分析 intset 的结构，其余函数都比较简单。

编码

无序集合类型有 OBJ _ENCODING_HT 和 OBJ _ENCODING_INTSET 两种编码，使用 dict 或 intset 存储数据。使用

OBJ _ENCODING_HT 时，键存储集合元素，值为空。使用 OBJ_ENCODINGINTSET 编码需满足以下条件：

集合中只存在整数型元素。
集合元素数量小于或等于 server.set_max_intset_entries，该值可通过 set-max-intset-entries 配置项调整。

有序集合

有序集合即数据都是有序的。存储一组有序的数据，最简单的是一下两种结构：

数组，可以通过二分查找法查找数据，但插入数据的复杂度为 $\rm O(N)$ 。
链表，可以快速插入数据，但是无法使用二分查找，查找数据的复杂度为 $\rm O(N)$ 。

定义

William Pugh 发布的跳表论文

skiplist 是一个多层级的链表结构，具有如下特点：

上层链表是相邻下层链表的子集。
头结点层数不小于其他节点的层数。
每个节点 (除了头结点) 都有一个随机的层数。

如下图就是一个跳表结构：

假设 skiplist 中 k 层节点的数量是 k+1 层节点的 p 倍，那么 skiplist 可以看成一棵平衡的 p 叉树，从顶层开始查找某个节点需要的时间是 $\rm O(logpN)$ 。注意，skiplist 中的每个节点都有一个随机的层数，它使用的是一种概率平衡而不是精准平衡。

在 skiplist 中查找数据，需要从最高层开始查找。如果某一层后驱节点元素已经大于目标元素（或者不存在后驱节点），则下降一层，从下一层当前位置继续查找。

在下图中，假设我们要找值为 19 的节点，他的搜索路径如下图所示：

查找步骤如下：

从链表头结点的最高层 level3 开始查找，找到节点 6。
本层节点没有后驱节点 (后驱节点为 NULL)，下降一层，即 levle2
节点 6 level2 的下一个节点值为 25，大于节点 19，下降一层，即 level1。
节点 6 level1 的下一个节点值为 9，小于节点 19，向右找到本层的下一个节点，即节点 9。
节点 9 level1 的下一个节点值为 25，大于节点 19，下降一层，即 level0。
节点 9 level0 的下一个节点值为 12，小于节点 19，向右找到本层的下一个节点，即节点 12。
节点 12 level0 的下一个节点值为 19，等于节点 19，找到 19 这个节点，可以返回啦。

在上面的例子中，假设查找的是值为 18 的节点会在找到 19 这个节点之后下降一层，但是 level0 已经是最底层了。就会导致查找失败。

在高层查找时，每向后移动一个节点，实际上会跨越低层多个节点，这样便大大提升了查找效率，最终达到二分查找的效率。

在 Redis 中，skiplist 节点 (server.h/zskiplistNode) 的定义如下：

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele; // 节点值
    double score; // 分数，用于排序节点
    struct zskiplistNode *backward; // 指向前驱节点，一个节点只有第一层有前驱节点指针。因此，skiplist 的第一层链表是一个双向链表
    struct zskiplistLevel {
        struct zskiplistNode *forward; // 指向本层的后驱节点指针
        unsigned long span; // 本层后驱节点跨越了多少个第一层节点，用于计算节点的索引值
    } level[];
} zskiplistNode;

skiplist 的定义如下：

typedef struct zskiplist {
    struct zskiplistNode *header, *tail; // 指向头，尾节点的指针
    unsigned long length; // 节点数量
    int level; // skiplist 最大的层数，最多为 ZSKIPLIST_MAXLEVEL(32) 层
} zskiplist;

根据 Redis 中 skiplist 节点的定义，我们不难画出其逻辑图：

Redis 源码版本：Redis-6.0.9，下面的内容涉及到的代码均在 t_zset.c 文件中。

`zslGetElementByRank`

函数功能：查找指定 rank 的节点。
参数：
- zskiplist *zsl：查找的 skiplist。
- unsigned long rank：查找的 rank 值。其中 rank 的范围是 $\rm 1\sim skilplist \space 中节点的数量$ (1 表示 skiplist 的第一个节点)。
返回值：查找成功返回该节点，查找失败返回 NULL。

/* Finds an element by its rank. The rank argument needs to be 1-based. */
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
    zskiplistNode *x; // 当前已经遍历到的节点
    unsigned long traversed = 0; // 遍历了多少个有效节点了
    int i;

    x = zsl->header; // 初始指向 skiplist 的头结点，skiplist 的 head 节点不存储有效数据的
    for (i = zsl->level-1; i >= 0; i--) { // zsl->level 是所有节点中的最大层数，从最高层到最底层的遍历顺序嘛
        // 当遍历过的有效节点数 <= 指定的 rank，循环执行
        while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
        {
            // span 记录遍历到 x 指向的节点跨越了多少个有效节点，即 x 及其之前有效节点的数量
            traversed += x->level[i].span; 
            // 更新 x
            x = x->level[i].forward;
        }
        
        // 当遍历过的节点数恰好是查找的 rank，说明就找到该索引的节点啦！例如：假设我们要获取 rank 为 3 的节点，遍历过了 3 个节点说明 x 指向的就是第三个有效节点
        if (traversed == rank) {
            return x; // 返回查找 
        }
    }
    
    // 走到这里说明没有找到哈
    return NULL;
}

`zslInsert`

函数功能：向 skiplist 中插入一个新节点。
参数：
- zskiplist *zsl：指定插入的 skiplist。
- double score：插入节点的 score 部分决定了插入到 skiplist 的位置。
- sds ele：插入的数据。
返回值：

#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^64 elements */

/* Insert a new node in the skiplist. Assumes the element does not already
 * exist (up to the caller to enforce that). The skiplist takes ownership
 * of the passed SDS string 'ele'. */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; // update 记录插入节点的前驱节点
    unsigned int rank[ZSKIPLIST_MAXLEVEL]; // 前驱节点的索引
    int i, level;

    serverAssert(!isnan(score)); // 这条语句不重要
    
    x = zsl->header; // 指向头结点
    
    // zsl->level 是所有节点中的最大层数，从最高层到最底层的遍历顺序嘛
    for (i = zsl->level-1; i >= 0; i--) { 
        /* store rank that is crossed to reach the insert position */
        // 如果 i == (zsl->level - 1) 即最高层，  rank[i] 初始化为 0
        // 如果 i != (zsl->level - 1) 即非最高层，rank[i] 初始化为上一层跨越的节点数
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        
        // x 节点的当前层有后驱节点 && (x 节点的 score 小于插入 score || 他俩 score 相等但是 x 的 sds 小于插入的 sds)
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            rank[i] += x->level[i].span; // 加上从 x 节点当前层的下一个节点跳跃的节点数，更新索引
            x = x->level[i].forward; // 更新 x
        }
        update[i] = x; // 记录插入节点第 i 层的前驱节点
    }
    /* we assume the element is not already inside, since we allow duplicated
     * scores, reinserting the same element should never happen since the
     * caller of zslInsert() should test in the hash table if the element is
     * already inside or not. */
    level = zslRandomLevel(); // 生成一个随机的层数
    
    // 如果新节点生成的随机层数大于原 skiplist 的最大层数，添加更高层的前驱节点和前驱节点的索引
    // 创建 skiplist 时已经为头结点预先分配了 ZSKIPLIST_MAXLEVEL 层的内存大小，这里就不需要再重新分配内存了
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0; // 高出 zsl->level 的前驱节点索引一定是 0
            update[i] = zsl->header; // 高出 zsl->level 的前驱节点一定是 zsl->header
            update[i]->level[i].span = zsl->length; // 初始化高出 zsl->level 层的 span
        }
        zsl->level = level; // 更新 zsl->level
    }
    x = zslCreateNode(level,score,ele); // 创建一个新的 skiplistNode 准备插入
    for (i = 0; i < level; i++) {
        x->level[i].forward = update[i]->level[i].forward; // 让新节点指向插入位置的当前层的后驱节点
        update[i]->level[i].forward = x; // 插入位置的当前层的前驱指针指向新插入的节点

        /* update span covered by update[i] as x is inserted here */
        // [1](见注解1)
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    // 这里更新的是哪些节点的 span 字段呢？其实就是那些节点的层数比新插入节点层数高的并且在新插入节点前面的那些节点
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++; // 插入了一个新的节点，当前层到后驱节点跨越的节点熟练自然要加 1 
    }

    // 设置新插入节点的 backward 字段，如果插入节点的索引值为 1 backward 字段设置为 NULL，否则指向第一层的前驱节点就行了
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    
    // 如果新插入的节点不是 skiplist 的最后一个节点，自然也要更新后驱节点的 backward 字段啦
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else // 否则呢，就需要更新 skiplist 的 tail 字段啦！
        zsl->tail = x;
    zsl->length++; // skiplist 中节点的数量加 1 
    return x; // 返回新插入的节点
}

我们来看看这两条语句是怎么更新新节点每一层的 span 和前驱节点每一层的 span 的哈！如下图，我们在一个 skiplist 中插入一个新的节点，其中节点 1 并不表示 skiplist 的头节点哈！ (下面的这个图用来举例似乎有点特殊，更加一般的情况需要单独想想啦！)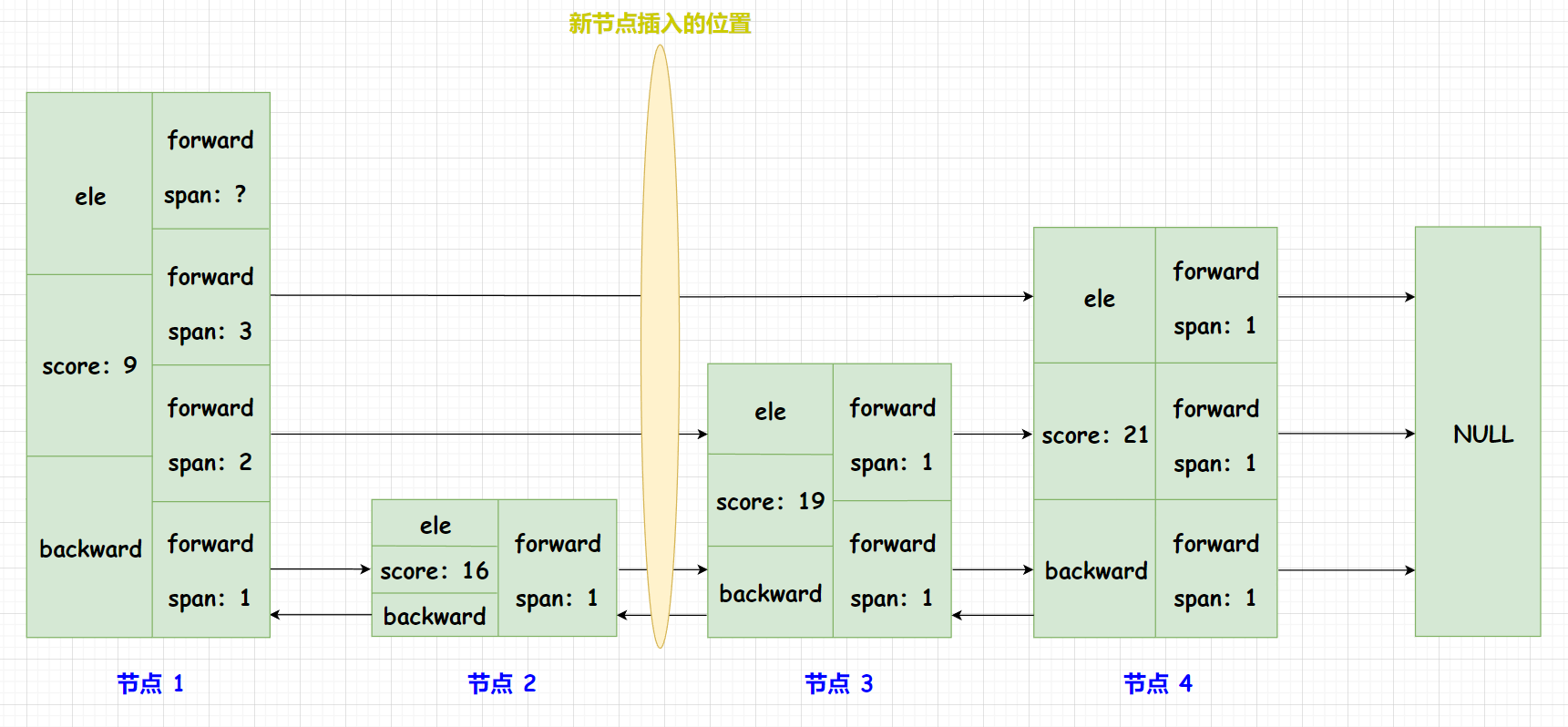

x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i])：
- rank[0]：表示第 0 层前驱节点的索引，也就是节点 2 及其之前所有有效节点的个数 (头结点不存数据，不是有效节点)。
- rank[i]：表示第 i 层前驱节点的索引。例如：当我们更新第一层的 span 时，其为 rank[1] ，如图表示节点 1 及其之前所有有效节点的个数。
- (rank[0] - rank[i]) 表示的是新插入节点当前层的前驱节点到新插入节点之间的节点数量 (不包括前驱节点)。
- update[i]->level[i].span：表示的是新插入节点当前层的前驱节点到当前层后驱节点跨越的节点数量。
- x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i])：就能计算出新插入节点到当前层的后驱节点跨越的节点数量啦！
update[i]->level[i].span = (rank[0] - rank[i]) + 1;：(rank[0] - rank[i]) 表示的是新插入节点当前层的前驱节点到新插入节点之间的节点数量 (不包括前驱节点)。加上新插入的节点，自然就是前驱节点的 span 啦！

`zslRandomLevel`

函数功能：生成一个随机的节点层数
参数：无。
返回值：生成的随机层数。

#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^64 elements */

int zslRandomLevel(void) {
    int level = 1;
    
    // [1](见注解1)
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL; // 如果生成的节点层数小于 32 直接返回即可，否则直接返回 32
}

这个代码块就是生成随机层数的核心代码啦！
- (random()&0xFFFF)：相当于 random() % 0x010000 只是位运算的速度比取模运算更快！经过取模运算该表达式计算出的值就会在区间 $\rm [0, 0xFFFF]$ 随机分布。
- (ZSKIPLIST_P * 0xFFFF)：ZSKIPLIST_P 是一个固定的概率，Redis 中取的是 0.25。
- (random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)：根据计算结果可得，该表达式为 true 的概率只有 0.25。
根据这个代码块的逻辑，我们可以轻易计算生成 x 层节点的概率。设 ZSKIPLIST_P 为 p，而非一个具体的数字。
- x == 1 时：概率为 $(1 - p)$ 。
- x == 2 时：概率为 $\times (1-p)$ 。
- x == 3 时：概率为 $p^2 \times (1-p)$ 。
- ···
- 生成 x 层节点的概率为 $p^{x-1} \times (1-p)$ 。
从概率上来讲，Redis 的 skiplist 可以看成是一颗四叉树。
$\space 层与\space x - 1\space层出现概率的比值为：\frac{p^{x-1} \times (1-p)}{p^{x-2} \times (1-p)} = p = 0.25$

其他的函数这里就不做分析了，跳表的函数实现起来还是比较简单的！

红黑树也常用于维护有序数据，为什么 Redis 使用 skiplist 而不使用红黑树呢？

实现和维护的简单性：跳表的实现和维护相对较为简单。跳表通过多层级链表实现，代码逻辑较为直观，插入、删除和查找操作相对容易理解和实现。而红黑树是一种自平衡二叉搜索树，涉及复杂的旋转操作和颜色属性的维护，代码实现和调试相对更为复杂。
平均性能：虽然红黑树在最坏情况下可以保证 O(log N) 的时间复杂度，但在平均情况下，跳表的性能也能达到 O(log N)。对于 Redis 的典型工作负载和数据访问模式，跳表的平均性能表现足够好，并且实现更为简单，因此成为一个合理的选择。
顺序操作的性能：跳表在处理范围查询和顺序遍历时，性能优于红黑树。跳表的结构使得它在多层级上进行线性扫描更加高效，对于需要大量范围查询的应用场景（如有序集合的范围操作），跳表提供了较好的性能支持。
内存使用：跳表在内存使用上较为灵活，可以通过调整跳表的层数来控制内存的使用量。虽然红黑树的内存使用较为紧凑，但对于 Redis 来说，跳表的灵活性在某些场景下更具优势。
代码复杂性和调试：跳表的代码实现相对简洁，对于开源项目和社区开发来说，更易于理解、维护和调试。简洁的代码逻辑也减少了潜在的bug和维护成本。
历史因素：跳表的引入与 Redis 的历史开发背景有关。最初，Redis 的开发者选择了跳表，之后随着 Redis 的演进和成熟，跳表的表现一直足够令人满意，因此没有必要更换为红黑树。

编码

有序集合类型有 OBJ_ENCODING_ZIPLIST 和 OBJ_ENCODING_SKIPLIST 两种编码，使用 ziplist、skiplist 存储数据。

使用 OBJ_ENCODING_ZIPLIST 编码需满足以下条件：

有序集合元素数量小于或等于 serverzset_max_ziplist_entries，该值可通过 zset-max-ziplist-entries 配置项调整。
有序集合所有元素长度都小于或于 server.zset_max_ziplist_value，该值可通过 zset-max-ziplist-value 配置项调整。