这是一个关于偏序集的定理,事实上它也可以扩展到图论,dp等中,是一个很有意思的东西
偏序集
偏序集是由集合 S S S以及其上的一个偏序关系 R R R定义的,记为 ( S , R ) (S,R) (S,R)
偏序关系:
对于一个二元关系 R ⊂ S × S R\subset S\times S R⊂S×S,如果其满足:
- ∀ x ∈ S , x R x \forall x\in S,xRx ∀x∈S,xRx 自反性
- ∀ x , y ∈ S \forall x,y\in S ∀x,y∈S,若 x R y xRy xRy且 y R x yRx yRx,则 x = y x=y x=y 反对称性
-
x
R
y
,
y
R
z
→
x
R
z
xRy,yRz\rightarrow xRz
xRy,yRz→xRz 传递性
显然自然数集 N N N以及最常见的小于等于关系 ≤ \leq ≤, ( N , ≤ ) (N,\leq) (N,≤)就构成了一个偏序集
事实上 ( N ∗ , ∣ ) (N^*,|) (N∗,∣)也是一个偏序集,其中 ∣ | ∣表示正整数的整除关系
以下为了讨论方便,我们将 R R R简记为 ≤ \leq ≤,当然它可以指代小于等于关系之外的其它关系
此外, ∀ x , y ∈ S \forall x,y\in S ∀x,y∈S,如果 x ≤ y x\leq y x≤y或 y ≤ x y\leq x y≤x,那么我们就说它们是可比的,否则说它们是不可比的
定义完了偏序集,我们可以从图上来看看它具体的样子
哈斯图(Hasse 图)
考虑一个偏序集 ( S , ≤ ) (S,\leq) (S,≤), ∀ x , y ∈ S \forall x,y\in S ∀x,y∈S,如果 x ≤ y x\leq y x≤y且不存在 z S . T . x ≤ z ≤ y z\ S.T. \ x\leq z\leq y z S.T. x≤z≤y,我们称为 y y y覆盖 x x x,那么此时我们就连一条从 x x x指向 y y y的有向边,最后得到的图就称为这个偏序集 ( S , ≤ ) (S,\leq) (S,≤)的Hasse图
比如下图是
x
,
y
,
z
{x,y,z}
x,y,z的幂集关于包含关系得到的Hasse图
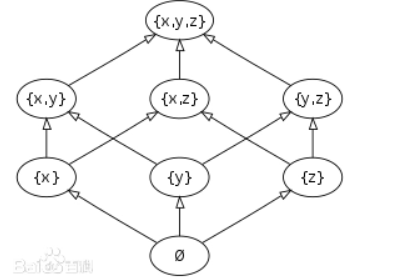
由于偏序关系满足了反对称性,所以Hasse图里面一定没有自环(否则就会合并成一个点),所以我们可以说Hasse图一定是一张DAG
其它偏序集的前置芝士
还是记我们要讨论的偏序集为 ( S , ≤ ) (S,\leq) (S,≤)
链:
偏序集中的一个全序子集。形式化地说,若集合
C
⊂
S
C\subset S
C⊂S,且
∀
a
,
b
∈
C
\forall a,b\in C
∀a,b∈C,
a
,
b
a,b
a,b是可比的,那么
C
C
C就是
S
S
S的一个链
链这个名字起的就很有水平,因为我们不难发现,偏序集中的一个全序子集,其在Hasse图中似乎就一定表现为一条链。比如上图中的
{
{
x
,
y
,
z
}
,
{
x
,
z
}
,
{
x
}
,
{
ϕ
}
}
\{\{x,y,z\},\{x,z\},\{x\},\{\phi\}\}
{{x,y,z},{x,z},{x},{ϕ}}就是一个全序子集,在图中刚好也表现成一条链。但我没有严格证明,这边搁置。
类似地,我们定义一个反链
反链:
若集合
C
⊂
S
C\subset S
C⊂S,且
∀
a
,
b
∈
C
\forall a,b\in C
∀a,b∈C,
a
,
b
a,b
a,b是不可比的,那么
C
C
C就是
S
S
S的一个反链
在图上看的话,
{
{
x
}
,
{
y
}
,
{
z
}
}
\{\{x\},\{y\},\{z\}\}
{{x},{y},{z}}就是一个反链
深度:
最长链大小
宽度:
最长反链大小
以上两个定义也是相当的形象。因为我们不难发现,如果把Hasse图按照偏序关系从低到高排列的话,链在图中往往就是一条竖着的,而反链是横着的,由此给出如上定义
最小链划分:
将集合
S
S
S划分为最少的若干个不相交的链
最小反链划分:
将集合
S
S
S划分为最少的若干个不相交的反链
Dilworth 定理
现在可以给出Dilworth 定理的具体内容了
Lemma1 对于任意有限偏序集,其最长反链大小必等于最小链划分中链的数目
其对偶形式也成立:
Lemma2 对于任意有限偏序集,其最长链大小必等于其最小反链划分中反链的数目
以下讨论均假定偏序集有限
总结以下:
最小链划分 = 最长反链大小 = 偏序集宽度
最小反链划分 = 最长链大小 = 偏序集深度
先来证Lemma2:
记定理中的最长链大小为n,我们对n做数学归纳法
显然n=1时定理成立
若n=k时定理成立,我们来证 n=k+1时定理成立
此时偏序集中的最长链长度为k+1,我们取出集合
S
S
S的所有极大元,组成集合
M
M
M,显然
M
M
M是一个反链,并且考虑
S
−
M
S-M
S−M,其最大链长一定为k(因为取出了所有的极大元),根据之前的归纳假设,
S
−
M
S-M
S−M的最小反链划分数目为 k,再加上M自己是一个反链,从而此时S的最小反链划分数为 k+1 = 最长链长度
□
\square
□
再来看Lemma1:
考虑偏序集
(
S
,
≤
)
(S,\leq)
(S,≤),记
∣
S
∣
=
m
|S|=m
∣S∣=m,我们对m进行归纳
m
=
1
m=1
m=1时Lemma1显然成立
若
m
=
k
m=k
m=k时定理成立,我们来证
m
=
k
+
1
m=k+1
m=k+1时定理成立:
设
A
A
A是集合
S
S
S的一条最长反链,记为
A
=
{
a
1
,
a
2
,
.
.
.
a
w
}
A = \{a_1,a_2,...a_w\}
A={a1,a2,...aw}
其中
∣
A
∣
=
w
|A|=w
∣A∣=w
我们取
D
(
A
)
=
{
x
∉
A
∣
∃
α
∈
S
,
x
≤
a
}
D(A) = \{x\notin A|\exists \alpha \in S,x\leq a\}
D(A)={x∈/A∣∃α∈S,x≤a}
U
(
A
)
=
{
x
∉
A
∣
∃
α
∈
S
,
a
≤
x
}
U(A) = \{x\notin A|\exists \alpha \in S,a\leq x\}
U(A)={x∈/A∣∃α∈S,a≤x}
显然
D
(
A
)
⋃
U
(
A
)
⋃
A
=
S
D(A)\bigcup U(A)\bigcup A = S
D(A)⋃U(A)⋃A=S
若存在最长反链
A
A
A使得
D
(
A
)
,
U
(
A
)
D(A),U(A)
D(A),U(A)均非空:
A
A
A是
S
S
S的最长反链,故
A
A
A也是
A
⋃
D
(
A
)
A\bigcup D(A)
A⋃D(A)的一个最长反链。注意到
∣
U
(
A
)
∣
≥
1
|U(A)|\geq 1
∣U(A)∣≥1,故
∣
A
⋃
D
(
A
)
∣
≤
k
|A\bigcup D(A)|\leq k
∣A⋃D(A)∣≤k,从而由归纳假设,
A
⋃
U
(
A
)
A\bigcup U(A)
A⋃U(A)可以划分为
w
w
w条链
c
1
,
c
2
,
.
.
.
c
w
c_1,c_2,...c_w
c1,c2,...cw,其中
c
i
c_i
ci的极大元是
a
i
a_i
ai.(这一点显然)
同理,
A
⋃
D
(
A
)
A\bigcup D(A)
A⋃D(A)也可以划分为
w
w
w条链
d
1
,
d
2
,
.
.
.
d
w
d_1,d_2,...d_w
d1,d2,...dw,其中
d
i
d_i
di的极小元是
a
i
a_i
ai
从而,我们就可以将
S
S
S划分为
w
w
w条链:
c
1
∪
d
1
,
.
.
.
.
c
w
∪
d
w
c_1\cup d_1,....c_w\cup d_w
c1∪d1,....cw∪dw
若对于任意最长反链
A
A
A,都有
D
(
A
)
=
ϕ
D(A)=\phi
D(A)=ϕ或
U
(
A
)
=
ϕ
U(A)=\phi
U(A)=ϕ
由假设,任一条反链
A
A
A必定构成全上界或者全下界。在
S
S
S中选一个极大元
y
y
y,再选一个极小元
x
x
x满足
x
≤
y
x\leq y
x≤y,
{
x
,
y
}
\{x,y\}
{x,y}构成一条链
C
C
C,从而在集合
S
−
C
S-C
S−C中,任一条最长反链的大小为
w
−
1
w-1
w−1(必定去除了一个元素),从而根据归纳假设,
S
−
C
S-C
S−C的最小链划分数为
w
−
1
w-1
w−1,再加上
C
C
C自己是一条链,故
S
S
S的最小链划分数为
w
w
w
□ \square □
应用举例
求一个序列的最大非递增序列长度以及其最少可以划分为多少个非递增序列
考虑由(位置,元素大小)这个二元组组成的集合,再定义一个偏序关系
<
<
<:
a
<
b
a<b
a<b当且仅当
a
a
a的位置<
b
b
b的位置且
a
a
a的值
<
b
<b
<b的值
从而这就构成了一个偏序集
(
s
,
<
)
(s,<)
(s,<),并且要求的分别就是集合的最长反链以及最小反链划分数
第一个问题可以直接dp即可,第二个问题,根据Dilworth 定理,实际上就是求偏序集的最长链大小,实际上也就是序列的LIS,非常妙的一个转化。
与DAG
之前说过,Hasse图就是一个DAG,而反过来,我们将DAG的点作为集合
S
S
S的元素,将偏序关系
≤
\leq
≤定义为点之间的可达性,就定义了一个偏序集
(
S
,
≤
)
(S,\leq)
(S,≤)
从而DAG上的最小可重路径覆盖(要求覆盖所有点)就等价于偏序集
(
S
,
≤
)
(S,\leq)
(S,≤)上的最小链覆盖
同理,将DAG上的有向边作为集合
T
T
T的元素,将偏序关系
≤
′
\leq'
≤′定义为边之间的可达性,就得到的另一个偏序集
(
T
,
≤
′
)
(T,\leq')
(T,≤′)
从而DAG上的最小可重路径覆盖(要求覆盖所有边)就等价于偏序集
(
T
,
≤
′
)
(T,\leq')
(T,≤′)上的最小链覆盖
Erdős–Szekeres 定理
含至少
r
s
+
1
rs+1
rs+1个元素的实数序列
{
a
}
\{a\}
{a}要么有一个长为
r
+
1
r+1
r+1的不下降子序列,要么有一个长为
s
+
1
s+1
s+1 的不上升子序列
Proof:
设序列长度为
n
≥
r
s
+
1
n\geq rs+1
n≥rs+1,定义偏序集
{
(
i
,
a
i
)
}
i
=
1
n
\{(i,a_i)\}_{i=1}^{n}
{(i,ai)}i=1n,其上的偏序关系
≤
\leq
≤定义为:
(
i
,
a
i
)
≤
(
j
,
a
i
)
⇔
(
i
≤
j
∧
a
i
≤
a
j
)
(i,a_i)\leq (j,a_i)\Leftrightarrow (i\leq j \ \wedge \ a_i\leq a_j)
(i,ai)≤(j,ai)⇔(i≤j ∧ ai≤aj)
假设该偏序集的宽度
≤
s
\leq s
≤s,则由Dilllworth定理可知其最小链覆盖数
≤
s
\leq s
≤s,若这些链的长度都
≤
r
\leq r
≤r,则总元素数
≤
r
s
<
r
s
+
1
≤
n
\leq rs< rs+1\leq n
≤rs<rs+1≤n
矛盾。
□
\square
□