本次实现的二叉搜索树并不是AVL数和红黑树，只是了解流程和细节。

二叉搜索树的概念

二叉搜索树并不是单纯存储数据。所以他有规则：
①.左子树比根小，右子树比根大。

②.搜索二叉树不建议用递归。

二叉搜索树一定要遵循这个规律！否则他都不能算是二叉搜索树！

K模型二叉搜索树的实现

二叉搜索树的架构

我们之前也学过二叉树，二叉树的结构是节点里面放了左右指针和值，所以节点就是一下结构。 而二叉树的本身就是又一个根节点连接起来的。

template<class T>
struct BinarySearchTreeNode
{
	BinarySearchTreeNode(T& key)
		:_key(key)
		, _left(nullptr)
		, _right(nullptr)
	{}
	T _key;
	BinarySearchTreeNode* _left;
	BinarySearchTreeNode* _right;
};
	template<class T>
	class BinarySearchTree
	{
	public:
		typedef BinarySearchTreeNode<T> Node;		
	private:
		Node* _root=nullptr;
	};

insert插入

插入一定要遵循规则：
①.左子树比根小，右子树比根大。 不是这个规则都不是二叉搜索树。

(1). 当你插入第一个值的时候，他就是根，所以我们要特殊处理，当_root==nullptr时，要把第一个插入的值变成根。
(2).除第一个值之后的值就要遵行规则。

bool insert(T& x)
{
	if (_root == nullptr)
	{
		Node* noeNode = new Node(x);
		_root = noeNode;
		return true;
	}
	Node* cur = _root;
	Node* parent = cur;
	while (cur)
	{
		if (cur->_key < x)
		{
			//大于在右边
			parent = cur;
			cur = cur->_right;

		}
		else if (cur->_key > x)
		{
			//小于在左边
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			//等于,二叉搜索树不允许冗余，所以直接返回false。
			return false;
		}

	}
	Node* newNode = new Node(x);
	if (newNode->_key > parent->_key)
		parent->_right = newNode;
	else
		parent->_left = newNode;
	return true;
}

find 查找

查找就很简单，只要把前面的代码复制一半，当查找到了，我们就返回true，到空了都没找到就返回false。

bool find(const T& x)
{
	Node* cur = _root;
	Node* parent = cur;
	while (cur)
	{
		if (cur->_key < x)
		{
			//大于在右边
			parent = cur;
			cur = cur->_right;

		}
		else if (cur->_key > x)
		{
			//小于在左边
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			//等于，找到了
			return true;
		}

	}
	return false;
}

中序遍历Inorder

中序遍历我们都很了解了，但是问题是，我们要把根传入，根一定是私有的，你在类外访问不了。这个时候我们就可以套一层。

public：
void Inorder()
{
	_Inorder(_root);
	cout << endl;
}
private:
	void _Inorder(Node* _root)
	{
		if (_root == nullptr) return;
		_Inorder(_root->_left);
		cout << _root->_key<< " ";
		_Inorder(_root->_right);
	}
	Node* _root=nullptr;

删除earse

删除其实很麻烦，有很多种情况。因为二叉搜索数一定是满足规则的，所以我们删除不能混乱了规则，而是继续保持规则。所以我们要用替换法，保证规则不乱。

替换法的思路

因为我们要保证规则不乱，那么我们可以用替换法，让左树的最大值/右树的最小值与当前值替换，因为当前节点的左边一定比他小，右边一定比他大，那么当我们用左边最大值，替换了当前节点，也不会改变规则；右边同理。

情况一 ：假如要删除节点左边是空的。

在左边时

假如我要删除9这个节点。并且左侧是空，那么我们是不是可以直接让他父亲的左边指向他的右边？思考一下！

为什么？左侧为空，当前删除节点的左侧一定是什么都没有的，右边可有可无，但是右边没有也没关系，一样置空，有的话，我们就需要让他的父亲链接他的孩子。

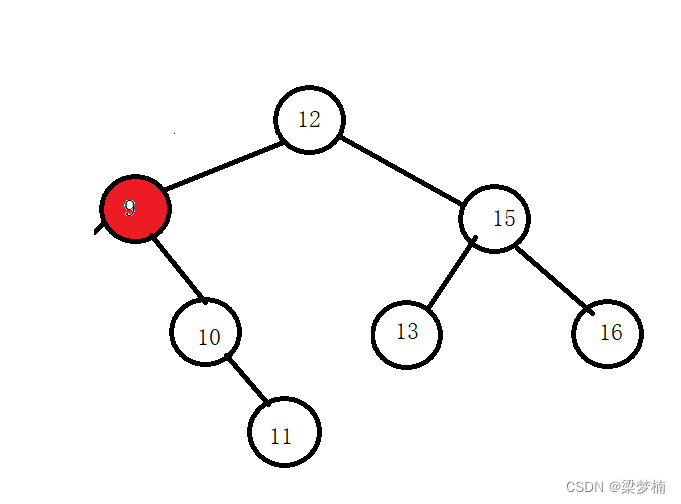
并且我们发现并不用替换法，就可以直接链接后删除。

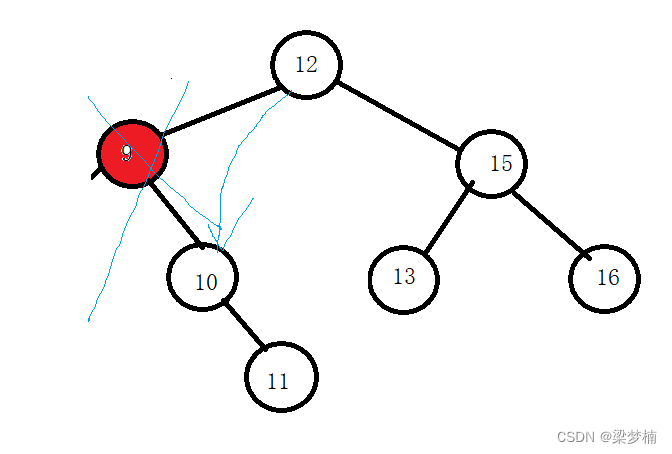
在右边时

其实在右边也是一样的，只不是我们要特殊判断一下，删除节点时父亲的左边还是右边，方便我们链接。

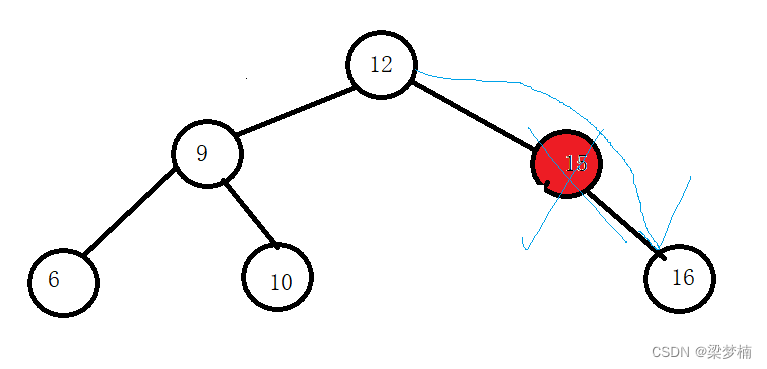
情况二：假如要删除节点右边是空的。

是父亲的右边时

那么他右边一定是没有值的，左边的值可有可无，那么我们就需要让它的父亲指向他的左值就可以了。

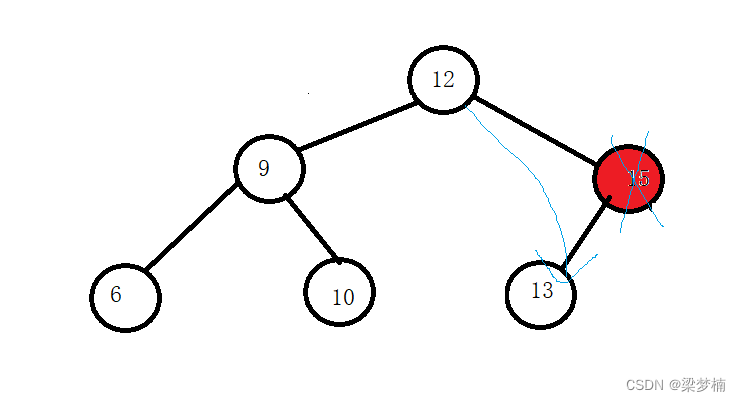
是父亲的左边时

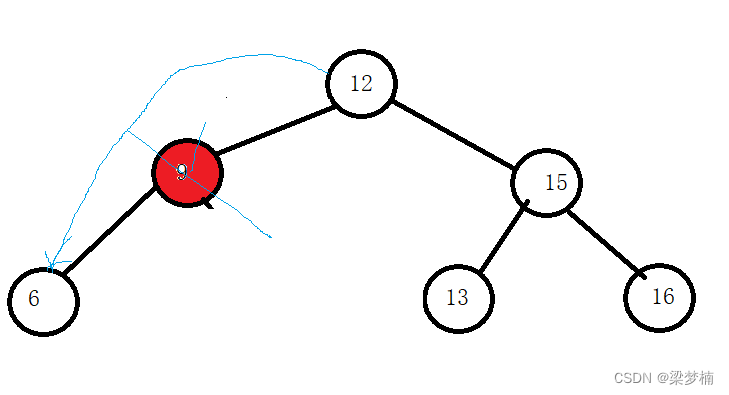
情况三：两边都有值

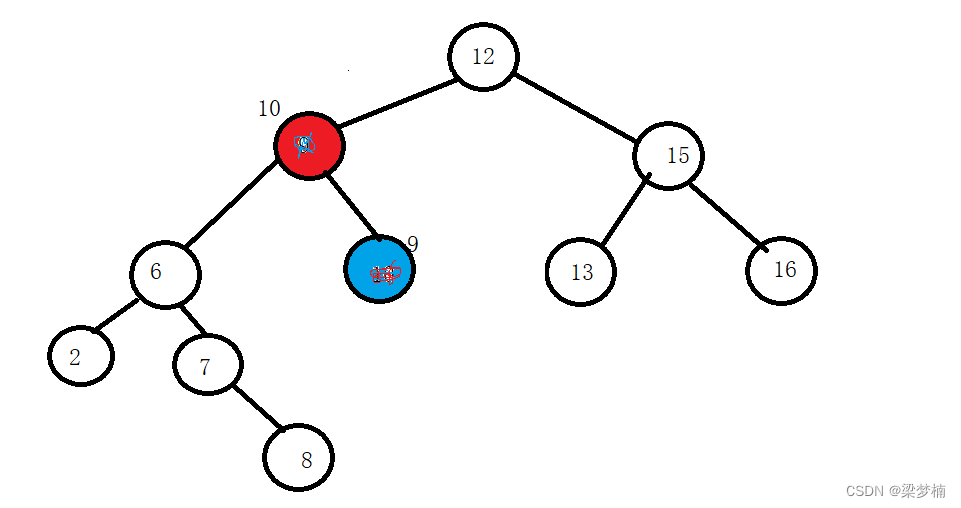
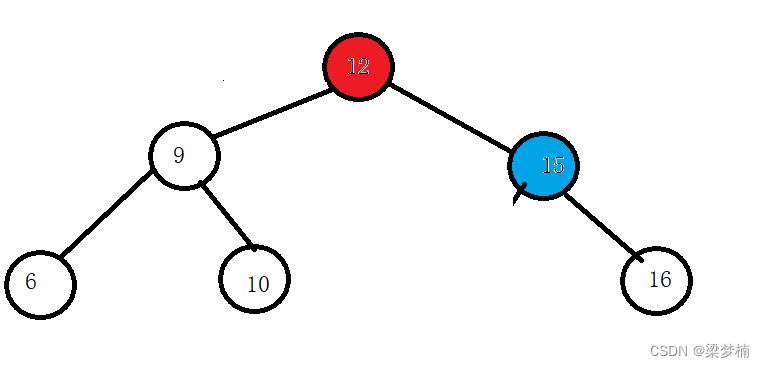
如果这棵树是这样的，那么我要删除9怎么做呢？就需要替换法，我们需要找左边最大值或者右边最小值，我们假设要找是右边最小值。

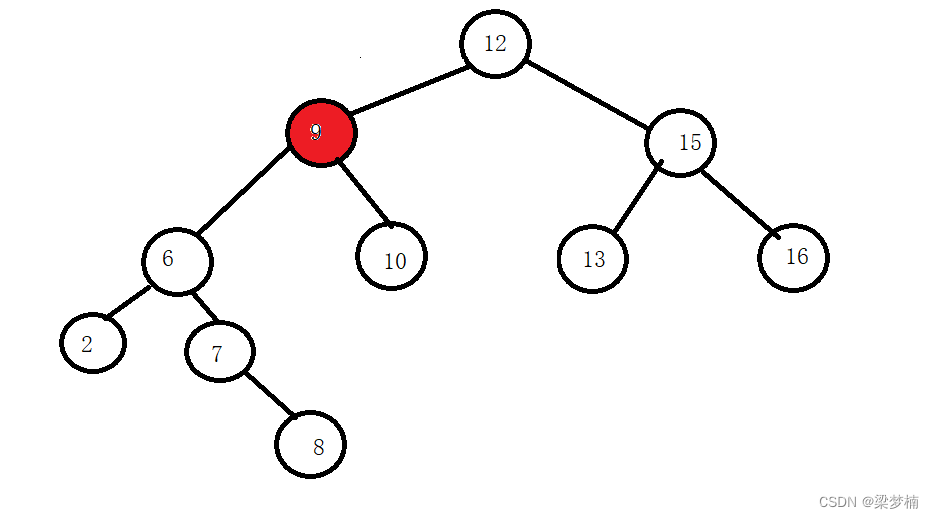
从当前节点开始找，右边最小值是10(蓝色标记)。

问：为什么要从当前节点找，而不是从根开始？
答：如果从根开始找，你会发现，当我们交换后，不满足条件了。图中右边最小值是13，如果换到最左边那就不满足二叉搜索的要求了，所以要从当前节点找，因为当前节点的右边跟当前这个位置换一定是比大，比其他节点小的。

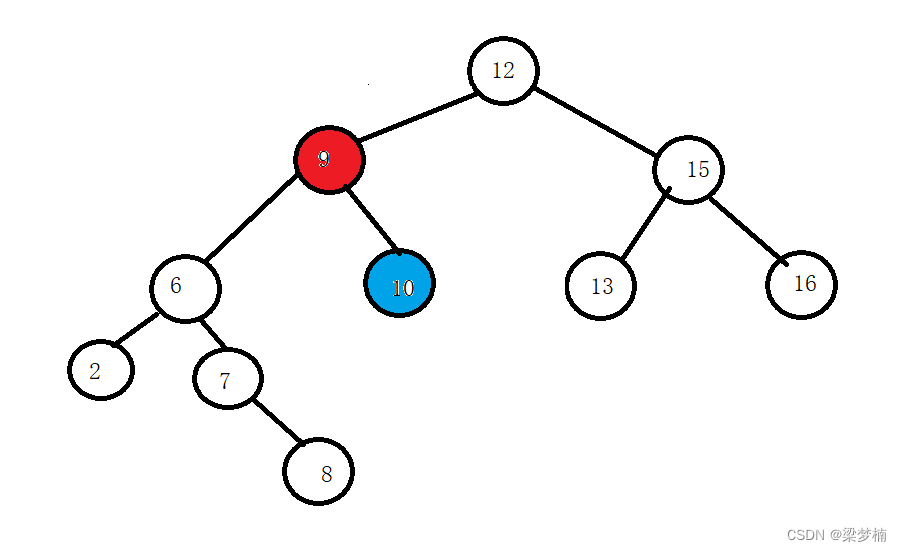
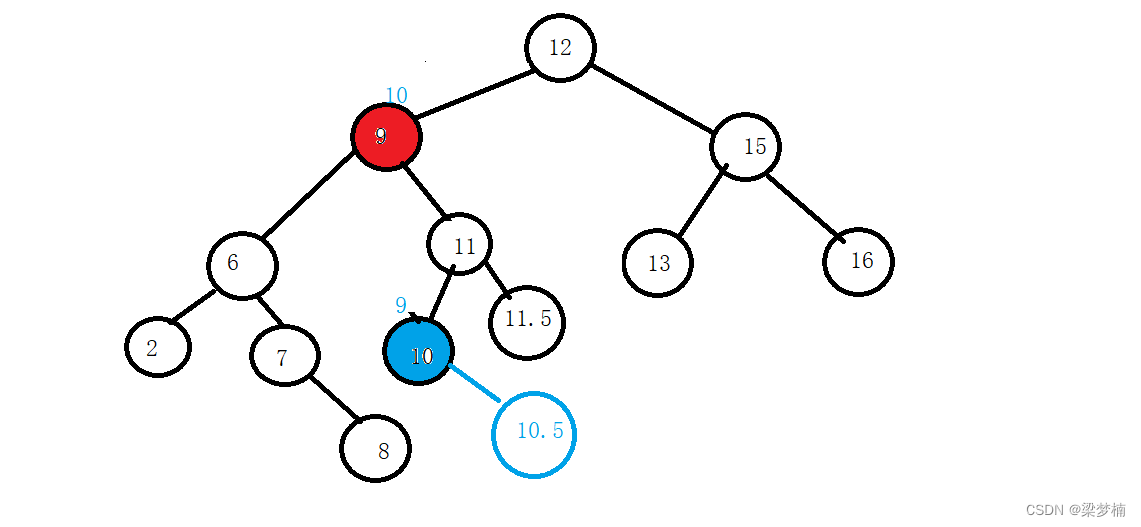
当我们都找到了，我们就要用交换法。将两个值交换后，左边最小的那个节点就是我们要删除的。那么我们就需要把最小节点的右边给它的右边。

左边

这里给大家道个歉，因为数字太过紧凑，所以凑不出数，只能让整型和浮点数混合了，在实际场景中是不可能有的，只是举个例子。

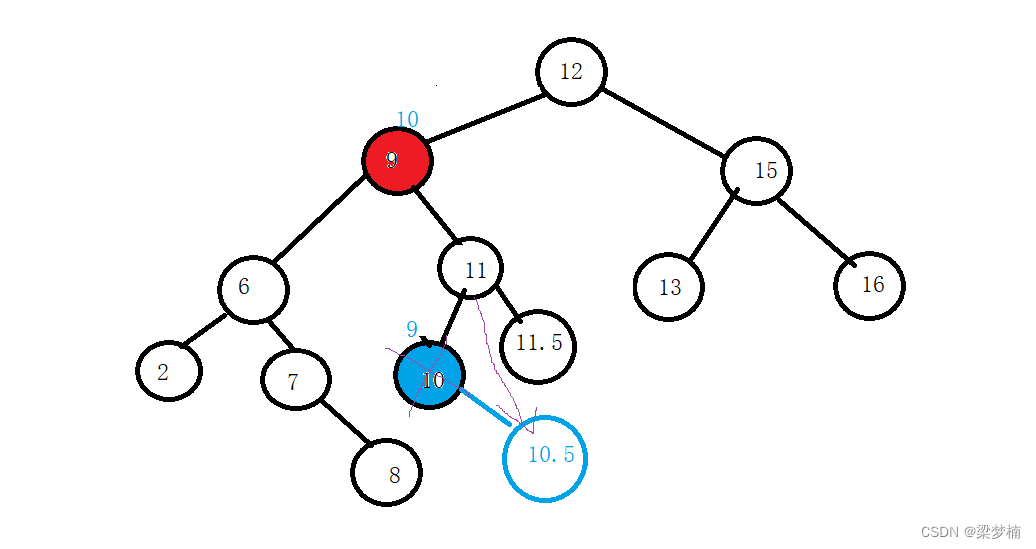
假设我们交换后，发现要删除的节点右边还有值，

问题：我怎么让被删除节点的父亲知道是左边还是右边的节点间接我的右节点呢？
答：需要判断一下，如果被删除的节点是父亲的左边，就需要让左边指向被删的右边，如果是父亲的右边就让父亲的右边指向被删的右边。

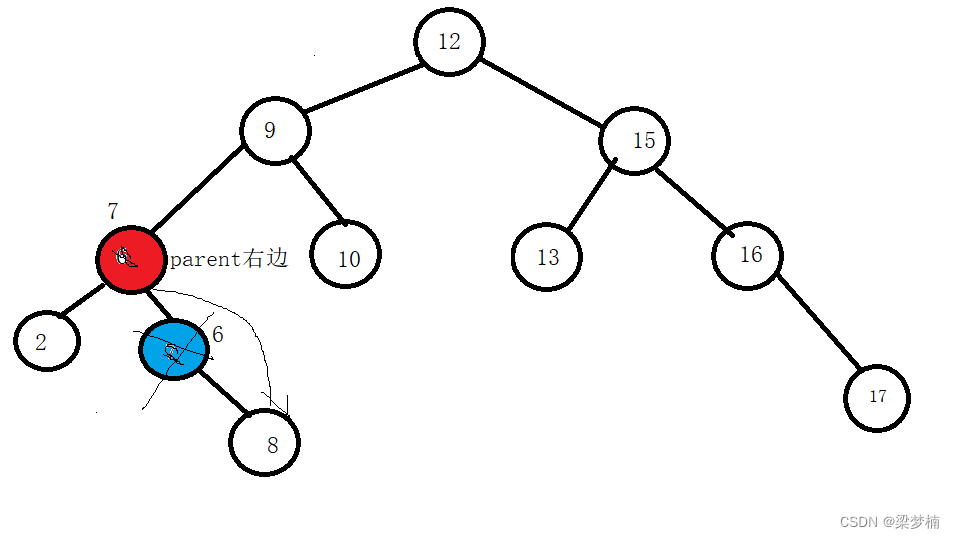
右边

这种情况，就是他在父亲的右边，所以我们需要让父亲的右边链接被删的右边。

代码实现

虽然删除的代码很复杂，但是要注意的细节很多。
(1).在我们找到了当前被删节点，情况三的时候，能不能让Node* rightMinParent = nullptr;? 答：不可以，因为当我们删除这种情况的时候，就会导致空指针访问，因为循环我们没有进去，但是链接值的时候，就会导致空指针访问。

(2).在我们交换后，能不能递归把他删了？不能！我问你交换后还满足二叉搜索数的要求吗？不满足，你永远都不会找到！

		bool erase(const T& x)
		{
			Node* cur = _root;
			Node* parent = cur;
			while (cur)
			{
				if (cur->_key < x)
				{
					//大于在右边
					parent = cur;
					cur = cur->_right;

				}
				else if (cur->_key > x)
				{
					//小于在左边
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					//等于，找到了

					if (cur->_left == nullptr)
					{
						//没有值直接删，把右边给父亲
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
							delete cur;
						}
						else if(cur == parent->_right)
						{
							parent->_right = cur->_right;
							delete cur;
						}
					}
					else if (cur->_right == nullptr)
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
							delete cur;
						}
						else if (cur == parent->_right)
						{
							parent->_right = cur->_left;
							delete cur;
						}
					}
					else
					{
						Node* rightMin = cur->_right;
						Node* rightMinParent = cur;
						//这里要让父亲是cur，删根的时候就会出问题
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						std::swap(cur->_key, rightMin->_key);
						if (rightMinParent->_left == rightMin)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;
						delete rightMin;
					}
					return true;
				}
			}
			return false;
		}