文章目录
- 1. 推导
- 2. 性质
- 3. 参考
1. 推导
r
r
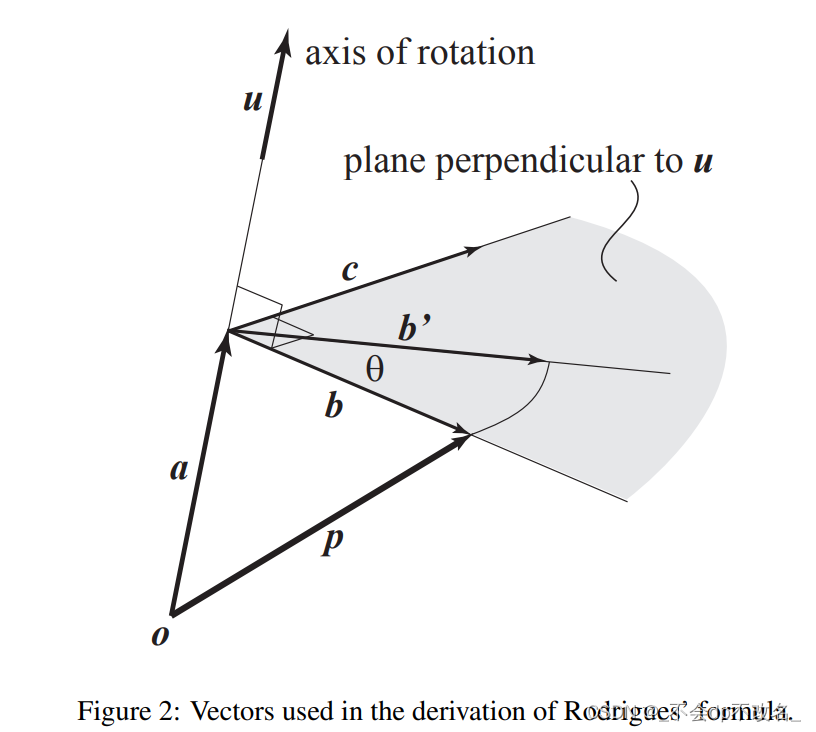
r为旋转轴,
θ
\theta
θ为旋转角度。
先将旋转轴单位化
u
=
r
∣
∣
r
∣
∣
u=\frac{r}{||r||}
u=∣∣r∣∣r
旋转可以被分为垂直和旋转两个方向,
我们求沿轴方向的分量其实就是在求
p
p
p向量在
u
u
u方向上的投影。
引用投影矩阵
P
=
A
(
A
⊤
A
)
−
1
A
⊤
P
u
=
u
(
u
⊤
u
)
−
1
u
⊤
u
⊤
u
=
I
P
u
=
u
u
⊤
P=A(A^{\top}A)^{-1}A^{\top}\\ P_u=u(u^{\top}u)^{-1}u^{\top}\\ u^{\top}u=I\\ P_u=uu^{\top}
P=A(A⊤A)−1A⊤Pu=u(u⊤u)−1u⊤u⊤u=IPu=uu⊤
其实也可以直接以向量的方式思考
u
⊤
p
=
u
∗
p
=
∣
∣
u
∣
∣
∣
∣
p
∣
∣
cos
α
u^{\top}p =u *p=||u|| \ ||p|| \cos \alpha
u⊤p=u∗p=∣∣u∣∣ ∣∣p∣∣cosα
还需要除
∣
∣
u
∣
∣
||u||
∣∣u∣∣
∣
∣
u
∣
∣
=
u
⊤
u
u
⊤
p
u
⊤
u
||u||=u^{\top}u \\ \frac{u^{\top}p}{u^{\top}u}
∣∣u∣∣=u⊤uu⊤uu⊤p
最后将值转换为向量
u
u
⊤
p
u
⊤
u
=
u
u
⊤
p
u\frac{u^{\top}p}{u^{\top}u}=uu^{\top}p
uu⊤uu⊤p=uu⊤p
令
a
a
a为
p
p
p在旋转轴
r
r
r上的分量
a
=
p
∥
=
u
u
⊤
p
a=p_{\parallel}=uu^{\top}p
a=p∥=uu⊤p
令
b
b
b为
p
p
p垂直旋转轴
r
r
r的分量
b
=
p
⊥
=
p
−
a
=
p
−
u
u
⊤
p
b=p_{\perp}=p-a=p-uu^{\top}p
b=p⊥=p−a=p−uu⊤p
令
c
=
u
×
p
c=u \times p
c=u×p,则
∣
∣
c
∣
∣
=
∣
∣
p
∣
∣
||c|| = ||p||
∣∣c∣∣=∣∣p∣∣
b b b旋转 θ \theta θ后得到 b ′ b' b′
b ′ = b cos θ + c sin θ b ′ = ( p − u u ⊤ p ) cos θ + u × p sin θ b'=b\cos \theta+c \sin \theta\\ b'=(p-uu^{\top}p) \cos \theta + u\times p \sin \theta b′=bcosθ+csinθb′=(p−uu⊤p)cosθ+u×psinθ
旋转后的
p
′
p'
p′
p
′
=
a
+
b
′
=
u
u
⊤
p
+
(
p
−
u
u
⊤
p
)
cos
θ
+
u
×
p
sin
θ
p'=a+b'=uu^{\top}p+(p-uu^{\top}p) \cos \theta + u\times p \sin \theta
p′=a+b′=uu⊤p+(p−uu⊤p)cosθ+u×psinθ
合并后得到
p
′
=
(
I
cos
θ
+
(
1
−
cos
θ
)
u
u
⊤
+
u
×
sin
θ
)
p
p'=(I \cos \theta+(1-\cos \theta)uu^{\top}+u_{\times}\sin \theta)p
p′=(Icosθ+(1−cosθ)uu⊤+u×sinθ)p
其中
u
×
u_{\times}
u×为叉乘矩阵
形式为
[
0
z
−
y
−
z
0
x
y
−
x
0
]
\begin{bmatrix} 0 & z & -y \\ -z & 0 & x \\ y & -x & 0 \end{bmatrix}
0−zyz0−x−yx0
所以旋转矩阵为
R
=
I
cos
θ
+
(
1
−
cos
θ
)
u
u
⊤
+
u
×
sin
θ
R=I\cos \theta+(1-\cos \theta)uu^{\top}+u_{\times} \sin \theta
R=Icosθ+(1−cosθ)uu⊤+u×sinθ
2. 性质
t
r
a
c
e
(
R
)
=
2
cos
θ
+
1
R
−
R
⊤
=
2
u
×
sin
θ
\begin{align} trace(R)=2 \cos \theta+1\\ R-R^{\top}=2u_{\times} \sin \theta \end{align}
trace(R)=2cosθ+1R−R⊤=2u×sinθ
性质一的证明,所有旋转矩阵都相似,构成一个正交群。
相似矩阵有性质
A
=
C
−
1
B
C
A=C^{-1}BC
A=C−1BC
所以所有旋转矩阵有相同的迹。
取其中一个旋转矩阵
[
cos
θ
−
sin
θ
0
sin
θ
cos
θ
0
0
0
1
]
\begin{bmatrix} \cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta &0\\ 0 & 0 & 1 \end{bmatrix}
cosθsinθ0−sinθcosθ0001
所以
t
r
(
R
)
=
2
cos
θ
+
1
tr(R)=2 \cos \theta+1
tr(R)=2cosθ+1
3. 参考
michigan_state_university
duke
math_stackchange