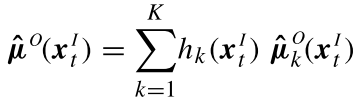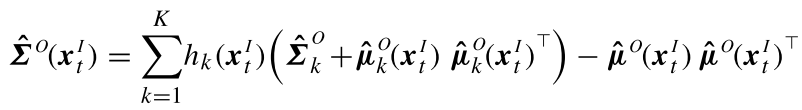机器人运动轨迹学习——GMM/GMR算法
-
前置知识
GMM的英文全称为:
Gaussian mixture model,即高斯混合模型,也就是说,它是由多个高斯模型进行混合的结果:当然,这里的混合是带有权重概念的。-
一维高斯分布
GMM中的个体就是高斯模型,说认真点就是高斯基函数,它还有另一个名字,径向基函数。
对于一维变量,其高斯分布为:
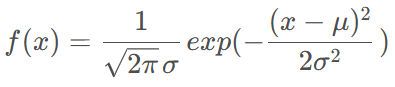
对应高斯概率密度的图形:
也就是说,对于一维变量x,它落在均值区间 [ u − σ , u + σ ] [u-\sigma, u+\sigma] [u−σ,u+σ]的概率为68.26%
-
多维高斯分布
多维 Gaussian 分布的概率密度函数为:
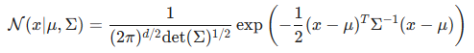
其中 μ \mu μ为均值向量, Σ \Sigma Σ为协方差矩阵
-
-
GMM对复杂轨迹的拟合
一个复杂运动的表达式可由一系列简单信号的加权组合表述,我们称这些简单信号为基函数;
一些流行的基函数有:
Radial Basis Functions (RBFs),Bernstein Basis Functions,Fourier Basis Functions其中,
Radial Basis Functions (RBFs),即径向基函数,一种应用如下图所示:通过为各基函数赋予不同的权重,生成了一条相对复杂的轨迹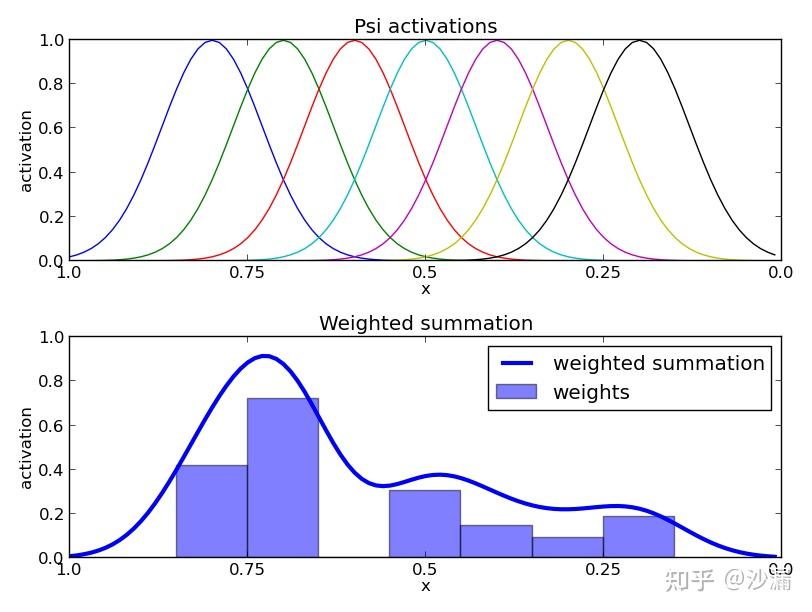
图片源自:Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 - 知乎 (zhihu.com)
-
GMR的回归思想
GMR(
Gaussian mixture regression)的思想:对于一个输入,借用GMM进行回归,回归的结果是一个高斯分布,
也就是说,我们回归得到的结果不是一个固定的值,而是一个概率值
以一维高斯分布为例:

我们回归得到的结果其均值为 μ \mu μ,在 [ u − σ , u + σ ] [u-\sigma, u+\sigma] [u−σ,u+σ]区间内的概率为68.26%
而且回归得到的这个高斯分布一般不是高斯混合分布中的某一个分布,而是一个新的分布
-
GMM的学习思想
根据我们的假设,GMM由多个高斯分布加权得到,那么GMM的概率密度函数为:
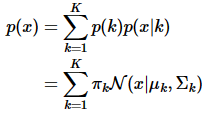
其中 p ( k ) = π k p(k)=\pi_k p(k)=πk是取第 k k k个高斯核的概率, p ( x ∣ k ) = N ( x ∣ u k , Σ k ) p(x|k)=N(x|u_k,\Sigma_k) p(x∣k)=N(x∣uk,Σk)是在第 k k k个高斯核下,取值x的概率
x可以是一个向量
因此,如果我们要从 GMM 的分布中随机地取一个点的话,实际上可以分为两步:
- 首先随机地在这 𝐾 个 高斯 之中选一个,每个 高斯 被选中的概率实际上就是它的系数 π k \pi_k πk ,
- 选中了 高斯 之后,再单独地考虑从这个 高斯 的分布中选取一个点就可以了
观察概率密度函数的形式,我们需要确定的参数为 π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk,μk,Σk
已知(假定)了概率密度函数的形式,而要估计其中的参数的过程被称作“参数估计”
-
GMM参数估计
-
思想
假设我们有一组数据点,假设他们服从分布p(x)(GMM中的一个高斯分布),我们要求其中的参数,
方法是直接假设一组参数,在这组参数( π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk,μk,Σk)下所确定的概率分布生成这组数据点的概率 π k \pi_k πk最大
即EM算法的思想
-
步骤一(E步,后验概率)
计算数据由每个高斯生成的概率:
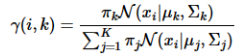
其中, π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk,μk,Σk取上一次迭代的值(或初始值)
-
步骤二(M步,估计相关的参数)
调整参数
对上面的公式进行对数似然,有:
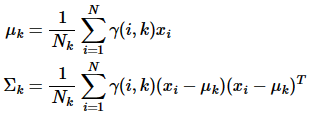
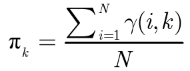
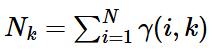 N是数据点的个数
N是数据点的个数
-
步骤三
重复上述步骤,直到满足我们的收敛条件(概率密度函数几乎不变)或超过设定的最大迭代次数
-
补充
我们注意到,在第一次执行上述步骤一时,参数 π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk,μk,Σk未知,这时我们需要给定一组初值,初值的好坏对收敛有影响,详情可参考漫谈 Clustering (3): Gaussian Mixture Model (pluskid.org)。
-
-
GMR参数回归
完成GMM模型的建立后,得到高斯混合模型:
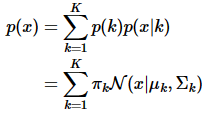
为了对给定参数进行回归,我们对其中的参数x,将其分为输入参数及输出参数,即有:
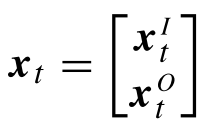
其中下标
t表示输入变量是t,输出变量可以是
t对应的二维坐标(x1,x2)根据GMR回归思想,对于均值和协方差,自然就分为:
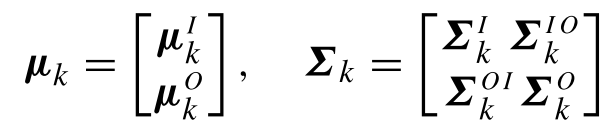
于是,直接根据公式,输入对单个高斯的回归,有:
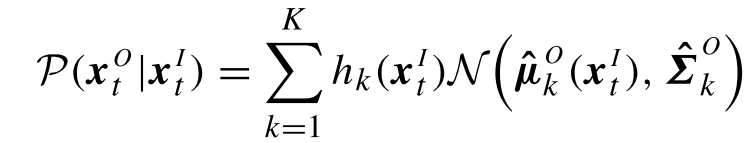
其中:
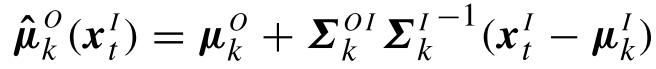
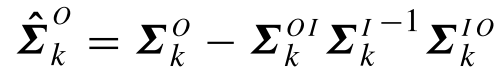
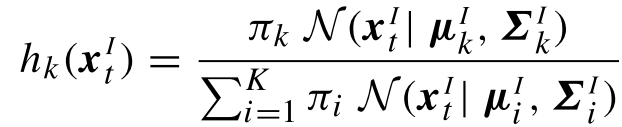
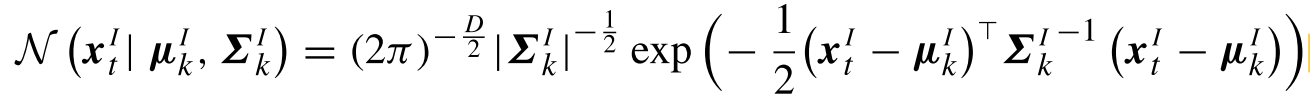
对于最终的结果,有: