总体标准差和样本标准差

一些表示上的差别。

总体标准差

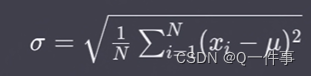
样本标准差

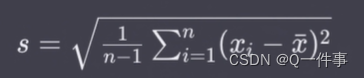
两者的区别

样本方差为什么除以n-1?

这主要是由于样本的方差会低估总体的方差（抽样的过程中，按照概率来说，会多选中间的数值从而低估方差），为了使样本标准方差与总体标准方差相接近，这就需要乘以一个大于1的数。）至于为什么是n-1？这据说是又叫贝塞尔修正（这个人算了很多种情况，发现n-1的效果最好）。

参考资料

样本方差为什么除以n-1?

这里面说到了无偏估计。

无偏估计

可以用下面的来解释。

在基础统计文章中，但凡用到总体标准差的时候，都用样本标准差直接替代总体标准差，这是有误差的，只不过样本容量大时，这个误差可以忽略不计。下面的参考文献中讲到了不同的估算方法。

从上表可以得出以下结果：

• 当样本容量n小时，各种方法的估计精度都不高，所以，要提高估计精度，样本容量应该足够大。
• 四种方法估计精度由高到低顺序为：常用估计、无偏估计、平均误差估计、无偏极值估计。尽管无偏估计的相对标准差稍大于常用估计，但它还是优于常用估计，因为它不存在系统误差。
• 当样本容量n小于10时，应用无偏估计，当n大于10时可采用常用估计，为计算简便且要求不高时可用无偏极差估计和平均误差估计。

虽然上面说了无偏估计，但是实际的无偏估计我依旧了解得不深。因而，我对相关概念进入深入探究。

无偏性与无偏估计量

笔者总结：看到这里，对于无偏估计我也大概了解了。

参考资料

如何理解和掌握总体标准差的估计方法及精度？

《概率论与数理统计》 浙大第四版