【学习笔记】Windows GDI绘图(四)矩阵Matrix详解

news2024/10/5 15:51:02

矩阵Matrix

基于矩阵在GDI绘图的重要性，所以想深入了学习矩阵的相关属性与方法。
先上个本文中所有的函数图例演示吧。
在这里插入图片描述
原型：

namespace System.Drawing.Drawing2D;

public sealed unsafe class Matrix : MarshalByRefObject, IDisposable

Matrix类封装了一个表示几何变换的 3x3 仿射矩阵。
在这里插入图片描述

在GDI+中，可以将仿射变换存储在一个Matrix对象中。由于第三列是固定的(0,0,1)，所以初始化一个Matrix时，只需要前两列的6个数字，如上图

Matrix myMatrix = new Matrix( 0, 1,
                             -1, 0,
                              3, 4);

注意，System.Drawing.Common 在.Net 6及之后的版本不支持在非Windows平台使用。

构造函数

Matrix()

原型：

public Matrix ();

初始一个单位矩阵（Identity Matrix）。

单位矩阵（Identity Matrix）
对角线上全是1：单位矩阵的主对角线上（从左上角到右下角）元素全是1。
非对角线上的元素全是0：除了主对角线上的元素，其他位置的元素全是0。

Matrix matrix=new Matrix();

Matrix:
	1	0
	0	1
	0	0

Matrix(Single, Single, Single, Single, Single, Single)

原型：

public Matrix (float m11, float m12, float m21, float m22, float dx, float dy);
参数说明
m11第1行、第1列
m12第1行、第2列
m21第2行、第1列
m22第2行、第2列
dx第3行、第1列
dy第3行、第2列
Matrix matrix = new Matrix(0, 1, -1, 0, 3, 4)

Matrix:
	0	1
	-1	0
	3	4

Matrix(Rectangle,Point[])和Matrix(RectangleF,PointF[])

原型：

public Matrix (System.Drawing.Rectangle rect, System.Drawing.Point[] plgpts);
public Matrix (System.Drawing.RectangleF rect, System.Drawing.PointF[] plgpts);

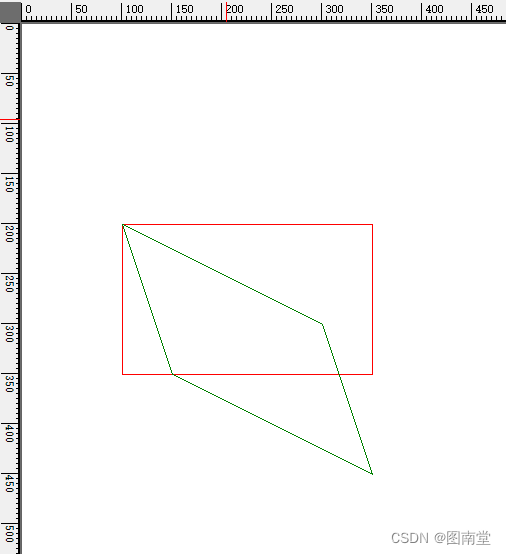
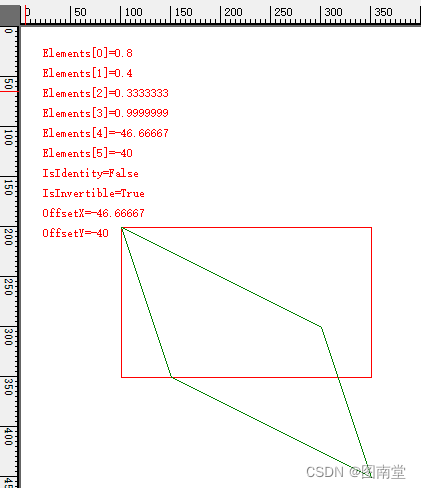
初始化由指定矩形和点集(3个点)的仿射变换矩阵。

参数说明
rect待变换的矩形
plgpts三个Point构成的数组，
分别表示变换后平行四边形的左上角、右上角和左下角三个点
右下角的点由上角三个点自动计算生成
//原矩形
e.Graphics.DrawRectangle(Pens.Red, rect);
using(GraphicsPath path=new GraphicsPath())
{
    path.AddRectangle(rect);
    using(Matrix matrix=new Matrix(rect,plgpts))
    {
        Console.WriteLine($"Matrix:\r\n{ToString(matrix, 6)}");
        /*Matrix:
         	0.800000	0.400000	
         	0.333333	1.000000	
         	-46.666670	-40.000000	
         */
        path.Transform(matrix);
        //变换的平行四边形
        e.Graphics.DrawPath(Pens.Green, path);
    }
}
/// <summary>
/// 格式化输出矩阵
/// </summary>
/// <param name="m"></param>
/// <param name="decimalPlaces"></param>
/// <returns></returns>
private string ToString(Matrix m, int decimalPlaces = 0)
{
    var elements = m.Elements;
    return $"\t{ToString(elements[0], decimalPlaces)}\t{ToString(elements[1], decimalPlaces)}\r\n" +
           $"\t{ToString(elements[2], decimalPlaces)}\t{ToString(elements[3], decimalPlaces)}\r\n" +
           $"\t{ToString(elements[4], decimalPlaces)}\t{ToString(elements[5], decimalPlaces)}\r\n";
}

/// <summary>
/// 格式化浮点型
/// </summary>
/// <param name="value">值</param>
/// <param name="decimalPlaces">小数点位数</param>
/// <returns></returns>
private string ToString(float value,int decimalPlaces=0)
{
    string format = $"F{decimalPlaces}";
    return value.ToString(format);
}

在这里插入图片描述

Matrix(Matrix3x2)

原型：

public Matrix (System.Numerics.Matrix3x2 matrix);

需要.NET高版本才支持，Matrix3x2的参数与Matrix(Single, Single, Single, Single, Single, Single)类似。

属性

Elements：矩阵元素值

原型：

public float[] Elements { get; }

获取表示该矩阵的浮点型数组，分别对应为m11, m12, m21, m22, dx, 和 dy 。

IsIdentity：是否为单位矩阵

原型：

public bool IsIdentity { get; }

获取当前矩阵是否为单位矩阵(主对角线为1，其他为0)

IsInvertible：是否可逆

原型：

public bool IsInvertible { get; }

获取当前矩阵是否可逆。

可逆矩阵：
1、方阵：矩阵的行数和列数相等的矩阵，例如 2×2，3×3 等。
2、行列式：方阵可以计算行列式，这是一个标量值，可以提供关于矩阵性质的信息。
3、可逆性：如果一个方阵的行列式不为零，那么这个矩阵是可逆的，也就是说存在一个逆矩阵，使得原矩阵与其逆矩阵相乘的结果为单位矩阵。

MatrixElements

原型：

public System.Numerics.Matrix3x2 MatrixElements { get; set; }

高版本才支持，与Elements类似。

OffsetX水平偏移

原型：

public float OffsetX { get; }

获取矩阵的 x 平移值（dx或第3行，第1列元素值)。

OffsetY垂直偏移

原型：

public float OffsetY { get; }

获取矩阵的 y 平移值（dx或第3行，第2列元素值)。
在这里插入图片描述

方法

Clone()

原型：

public System.Drawing.Drawing2D.Matrix Clone ();

var matrixClone= matrix.Clone();

Equals(Object) 值是否相等

原型：

public override bool Equals (object? obj);

判断两个Matrix的Elements值是否相等，是的话，返回True,否则返回的False。

using (Matrix matrix = new Matrix(0, 1, -1, 0, 3, 4))
using (Matrix otherMatrix = new Matrix(0, 1, -1, 0, 3, 4))
{
    var matrixClone= matrix.Clone();
    int offset = 20;
    DrawString(e,$"IsEquals:{matrix.Equals(matrixClone)}",ref offset);//true
    DrawString(e, $"IsEquals:{matrix.Equals(otherMatrix)}", ref offset);//true

    matrixClone.Translate(5, 6, MatrixOrder.Append);
    DrawMatrixElements(e, matrix, ref offset);
    DrawMatrixElements(e, matrixClone, ref offset);
    offset += 20;

    matrixClone.Dispose();
}

Invert() 反转

原型：

public void Invert ();

if(matrix.IsInvertible)//是否可逆
{
    DrawMatrixElements(e, matrix, ref offset);
    matrix.Invert();//反转
    DrawMatrixElements(e, matrix, ref offset);
}

Multiply相乘

原型：

public void Multiply (System.Drawing.Drawing2D.Matrix matrix);//默认Prepend
public void Multiply (System.Drawing.Drawing2D.Matrix matrix, System.Drawing.Drawing2D.MatrixOrder order);

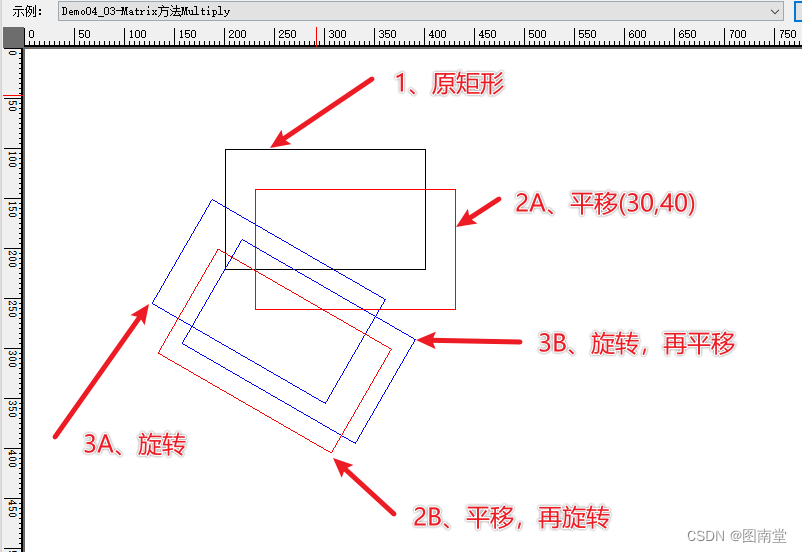
注意相乘的顺序

参数说明
orderAppend：原矩阵x新矩阵
Prepend：新矩阵x原矩阵(默认)
using (Matrix matrixA = new Matrix(1, 0, 0, 1, 30, 40))
using (Matrix matrixB = new Matrix(1, 0, 0, 1, 30, 40))
using (Matrix matrixRotate = new Matrix())
{
    //修改页面坐标
    e.Graphics.Transform = new Matrix(1, 0, 0, 1, 100, 100); 
    var rect = new Rectangle(100, 0, 200, 120);
    //1、原矩形
    e.Graphics.DrawRectangle(Pens.Black, rect);

    //顺时针旋转30度
    matrixRotate.Rotate(30, MatrixOrder.Append);

    using (GraphicsPath  path = new GraphicsPath())
    {
        path.AddRectangle(rect);

        var pathClone = (GraphicsPath)path.Clone();
        pathClone.Transform(matrixA);
        //2A、平移(30,40)后的矩形
        e.Graphics.DrawPath(Pens.Red, pathClone);

        pathClone = (GraphicsPath)path.Clone();
        pathClone.Transform(matrixRotate);
        //3A、旋转30度
        e.Graphics.DrawPath(Pens.Blue, pathClone);


        //相乘顺序： matrixRotate * matrixA,先旋转，再平移
        matrixA.Multiply(matrixRotate);

        pathClone = (GraphicsPath)path.Clone();
        pathClone.Transform(matrixA);
        //3B、先旋转，再平移
        e.Graphics.DrawPath(Pens.Blue, pathClone);


        //相乘顺序：matrixB * matrixRotate，先平移，再旋转
        matrixB.Multiply(matrixRotate, MatrixOrder.Append);

        pathClone = (GraphicsPath)path.Clone();
        pathClone.Transform(matrixB);
        //2B、先平移，再旋转
        e.Graphics.DrawPath(Pens.Red, pathClone);
    }
}

Multiply

Reset()重置

原型：

public void Reset ();

将矩阵重置为一个单位矩阵。

Rotate绕原点旋转

原型：

public void Rotate (float angle);//默认Prepend
public void Rotate (float angle, System.Drawing.Drawing2D.MatrixOrder order);

绕原点(0,0)旋转(正数：顺时针，负数：逆时针)

using (Matrix matrixRotate = new Matrix())
{
    var rect = new Rectangle(100, 100, 200, 120);
    //1、原矩形
    e.Graphics.DrawRectangle(Pens.Black, rect);

    //顺时针旋转30度
    matrixRotate.Rotate(30, MatrixOrder.Append);

    e.Graphics.Transform = matrixRotate;
    e.Graphics.DrawRectangle(Pens.Red, rect);

    matrixRotate.Reset();
    //逆时针旋转30度
    matrixRotate.Rotate(-30, MatrixOrder.Append);
    e.Graphics.Transform = matrixRotate;
    e.Graphics.DrawRectangle(Pens.Blue, rect);
}

Rotate

RotateAt绕某点旋转

原型：

public void RotateAt (float angle, System.Drawing.PointF point);
public void RotateAt (float angle, System.Drawing.PointF point, System.Drawing.Drawing2D.MatrixOrder order);

绕指定的点旋转

using (Matrix matrixRotate = new Matrix())
{
    var rect = new Rectangle(100, 100, 200, 120);
    var center = new PointF((rect.Left + rect.Right) / 2f, (rect.Top + rect.Bottom) / 2f);
    //1、原矩形
    e.Graphics.DrawRectangle(Pens.Black, rect);

    //顺时针旋转45度
    matrixRotate.RotateAt(30, center, MatrixOrder.Append);

    e.Graphics.Transform = matrixRotate;
    e.Graphics.DrawRectangle(Pens.Red, rect);

    matrixRotate.Reset();
    //逆时针旋转45度
    matrixRotate.RotateAt(-30, center,MatrixOrder.Append);
    e.Graphics.Transform = matrixRotate;
    e.Graphics.DrawRectangle(Pens.Blue, rect);
}

在这里插入图片描述

Scale缩放

原型：

public void Scale (float scaleX, float scaleY);
public void Scale (float scaleX, float scaleY, System.Drawing.Drawing2D.MatrixOrder order);

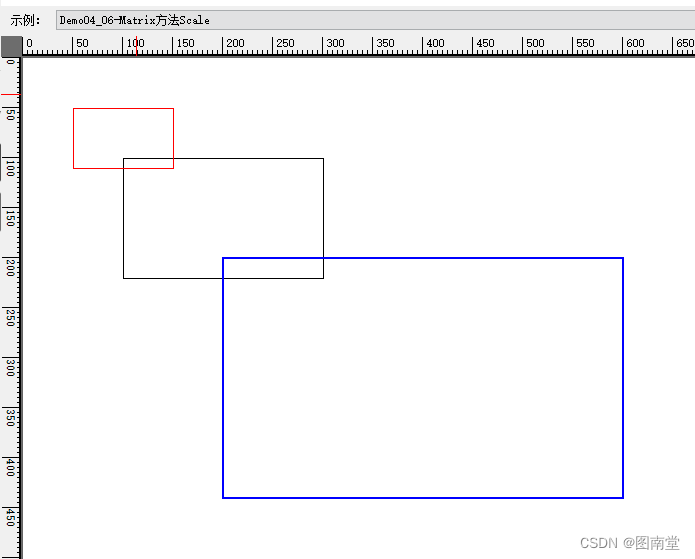
对矩阵设置水平、垂直缩放。

using (Matrix matrixScale = new Matrix())
{
    var rect = new Rectangle(100, 100, 200, 120);
    //1、原矩形
    e.Graphics.DrawRectangle(Pens.Black, rect);

    //水平、垂直各缩小1倍
    matrixScale.Scale(0.5f, 0.5f, MatrixOrder.Append);

    e.Graphics.Transform = matrixScale;
    e.Graphics.DrawRectangle(Pens.Red, rect);

    matrixScale.Reset();
    //水平、垂直各放大1倍
    matrixScale.Scale(2, 2, MatrixOrder.Append);
    e.Graphics.Transform = matrixScale;
    e.Graphics.DrawRectangle(Pens.Blue, rect);
}

在这里插入图片描述

Shear剪切

原型：

public void Shear (float shearX, float shearY);
public void Shear (float shearX, float shearY, System.Drawing.Drawing2D.MatrixOrder order);

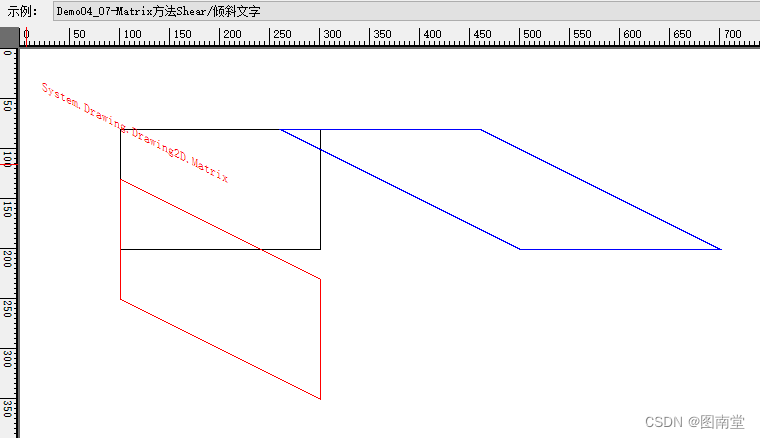
Shear变换（剪切变换）是一种几何变换，通常用于计算机图形学和图像处理领域。它通过在一个方向上平行移动各点的位置来改变图形的形状，而不改变其面积。这种变换在视觉上会使图形看起来像是被拉伸或压缩了。
在这里插入图片描述
仅当其中一个参数为0时，此方法中应用的变换才是纯剪切。
可用于绘制倾斜的文字。

 using (Matrix matrix = new Matrix())
{
    var rect = new Rectangle(100, 80, 200, 120);
    //1、原矩形
    e.Graphics.DrawRectangle(Pens.Black, rect);

    //垂直剪切(x'=x,y'=y+k*x)
    //原左上角(100,80)=>平行四边形左上角，x不变100，y=80+100*0.5=130,即：(100,130)
    //原右上角(300,80)，x不变，y=80+300*0.5=230,即(300,230)
    matrix.Shear(0, 0.5f, MatrixOrder.Append);

    e.Graphics.Transform = matrix;
    e.Graphics.DrawRectangle(Pens.Red, rect);
    //绘制倾斜的文字 
    int offset = 20;
    DrawString(e, matrix.ToString(), ref offset);

    matrix.Reset();
    //水平剪切(x'=x+ky,y'=y)
    matrix.Shear(2, 0, MatrixOrder.Append);
    e.Graphics.Transform = matrix;
    e.Graphics.DrawRectangle(Pens.Blue, rect);
}

在这里插入图片描述

TransformPoints应用变换到点集中

原型：

public void TransformPoints (System.Drawing.Point[] pts);
public void TransformPoints (System.Drawing.PointF[] pts);
public void VectorTransformPoints (System.Drawing.Point[] pts);

将仿射变换应用到给点的Point数组中

//定义多个点构成一个矩形,(100,80,200,120);
    var points = new Point[]
    {
        new Point(100,80),
        new Point(300,80),
        new Point(300,200),
        new Point(100,200),
        new Point(100,80)
    };
    //1、原矩形
    e.Graphics.DrawLines(Pens.Black, points);

    using (var matrix = new Matrix())
    {
        matrix.Scale(0.5f, 2, MatrixOrder.Append);
        //变换矩形应用到点集上
        matrix.TransformPoints(points);
        e.Graphics.DrawLines(Pens.Red, points);
    }

在这里插入图片描述

TransformVectors应用变换到点集中(忽略平移)

原型：

public void TransformVectors (System.Drawing.Point[] pts);
public void TransformVectors (System.Drawing.PointF[] pts);

就矩阵(忽略平移，第三行)应用到点集上

using (Matrix matrixScale = new Matrix())
{
    //定义多个点构成一个矩形,(100,80,200,120);
    var points = new Point[]
    {
        new Point(100,80),
        new Point(300,80),
        new Point(300,200),
        new Point(100,200),
        new Point(100,80)
    };
    //1、原矩形
    e.Graphics.DrawLines(Pens.Black, points);

    using (var matrix = new Matrix())
    {

        matrix.Rotate(30, MatrixOrder.Append);
        matrix.Scale(0.5f,0.5f, MatrixOrder.Append);
        matrix.Translate(100, 50);
        //变换矩形应用到点集上
        var ptsClone = points.Clone() as Point[];
        matrix.TransformPoints(ptsClone);
        e.Graphics.DrawLines(Pens.Red, ptsClone);

        //忽略平移
        matrix.TransformVectors(points);
        e.Graphics.DrawLines(Pens.Blue, points);
    }
}

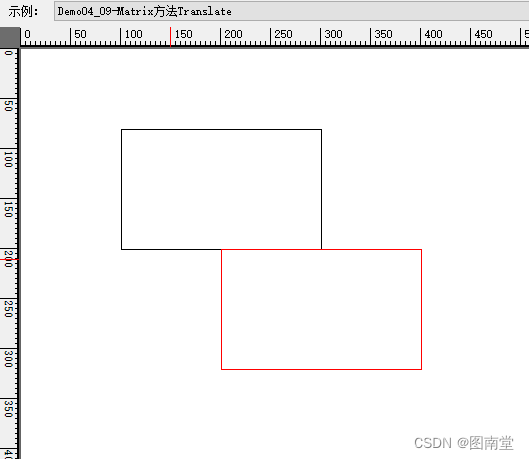
在这里插入图片描述

Translate平移

原型：

public void Translate (float offsetX, float offsetY);
public void Translate (float offsetX, float offsetY, System.Drawing.Drawing2D.MatrixOrder order);

平移矩阵

var rect = new Rectangle(100, 80, 200, 120);
//1、原矩形
e.Graphics.DrawRectangle(Pens.Black, rect);

using(var matrix=new Matrix())
{
    //平称矩阵
    matrix.Translate(100, 120, MatrixOrder.Append);
    e.Graphics.Transform = matrix;
    e.Graphics.DrawRectangle(Pens.Red, rect);
}

在这里插入图片描述

https://learn.microsoft.com/en-us/dotnet/fundamentals/runtime-libraries/system-drawing-drawing2d-matrix
https://learn.microsoft.com/en-us/dotnet/api/system.drawing.drawing2d.matrix?view=net-8.0

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1690756.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

玩机社区 - 2024年最美社区源码开源

玩机社区 - 2024年最美社区源码开源

玩机社区 - 2024年最美社区源码开源 教程源码文档都内置到压缩包了 https://pan.baidu.com/s/1xwcscTne-JMbmKEntiuAuA?pwd78oi
阅读更多...
22个C语言小白常见问题总结

22个C语言小白常见问题总结

一.语言使用错误 在打代码的过程中&#xff0c;经常需要在中文与英文中进行转换&#xff0c;因此常出现一些符号一不小心就用错&#xff0c;用成中文。例如&#xff1a;“&#xff1b;”中文中的分号占用了两个字节&#xff0c;而英文中“;”分号只占用一个字节。编译器只能识…
阅读更多...
遥感和ENVI技术检测食物污染

遥感和ENVI技术检测食物污染

对于生产者和消费者来说食物污染都是个问题。家禽污染会引发严重的健康问题&#xff0c;导致严重的危害。美国农业部需要一种方法&#xff0c;使用遥感影像在离开生产线之前探测出受污染的家禽。 解决方案 提起遥感&#xff0c;人们想到的大多是那些太空船和轨道卫星。然而在美…
阅读更多...
电脑版网易云音乐听歌识曲

电脑版网易云音乐听歌识曲

文章目录 流程 流程 电脑网易云音乐的搜索框旁边就是听歌识曲功能
阅读更多...
基于PHP的物业管理的设计与实现

基于PHP的物业管理的设计与实现

第1章 绪论... 1 1.1 研究背景与意义... 1 1.2 国内外发展现状... 2 第2章 关键技术介绍... 3 2.1 PHP语言... 3 2.2 MySQL数据库... 3 2.3 Zend框架... 4 2.4 B/S架构... 4 第3章 系统需求分析... 5 3.1 可行性分析... 5 3.1.1 技术可行性分析... 5 3.1.2 经济可行…
阅读更多...
Spring6基础笔记

Spring6基础笔记

Spring6 Log4j2 1、概述 1.1、Spring是什么&#xff1f; Spring 是一款主流的 Java EE 轻量级开源框架 &#xff0c;Spring 由“Spring 之父”Rod Johnson 提出并创立&#xff0c;其目的是用于简化 Java 企业级应用的开发难度和开发周期。Spring的用途不仅限于服务器端的开发…
阅读更多...
某大型制造集团企业信息化建设总体规划设计方案(67页PPT)

某大型制造集团企业信息化建设总体规划设计方案(67页PPT)

方案介绍&#xff1a; 随着信息技术的飞速发展&#xff0c;企业信息化建设已成为提高管理效率、增强企业竞争力的重要手段。某大型制造集团为应对市场变化、提升管理水平、优化资源配置&#xff0c;决定进行全面深入的信息化建设。本方案旨在构建一个集生产、管理、销售、物流…
阅读更多...
C语言 浮点数 打印的方法

C语言 浮点数 打印的方法

一、方式1 在C语言中&#xff0c;浮点数&#xff08;通常包括 float 和 double 类型&#xff09;的打印是通过标准库中的 printf 函数完成的。为了正确地打印浮点数&#xff0c;需要使用格式说明符来指定如何格式化输出。 #include <stdio.h> int main(void) { floa…
阅读更多...
常见的字符编码

常见的字符编码

字符&#xff1a;各种文字和符号的总称&#xff0c;包括各个国家的文字&#xff0c;标点符号&#xff0c;图形符号&#xff0c;数字等 字符集&#xff1a;字符集是多个符号的集合&#xff0c;每个字符集包含的字符个数不同 字符编码&#xff1a;字符集只是规定了有哪些字符&a…
阅读更多...
从零开始写 Docker(十五)---实现 mydocker run -e 支持环境变量传递

从零开始写 Docker(十五)---实现 mydocker run -e 支持环境变量传递

本文为从零开始写 Docker 系列第十五篇&#xff0c;实现 mydocker run -e, 支持在启动容器时指定环境变量&#xff0c;让容器内运行的程序可以使用外部传递的环境变量。 完整代码见&#xff1a;https://github.com/lixd/mydocker 欢迎 Star 推荐阅读以下文章对 docker 基本实现…
阅读更多...
《我的阿勒泰》观后感（一、什么叫做有用）

《我的阿勒泰》观后感（一、什么叫做有用）

通过央视热播短剧《我的阿勒泰》&#xff0c;认识了李娟老师。同时也认识了她的作品&#xff0c;值得推荐。 生命并不荒凉&#xff0c;它是一种安静的绝美。 生活&#xff0c;如同一个巨大的迷宫&#xff0c;充满了未知和变数。有时&#xff0c;我们会在其中迷失方向&#xf…
阅读更多...
STM32通用定时器的应用实例（基于STM32F103）

STM32通用定时器的应用实例（基于STM32F103）

目录 概述 1 STM32Cube配置项目 1.1 准备环境 1.2 配置项目参数 1.3 生成Project 2 HAL函数 2.1 初始化函数&#xff1a;HAL_TIM_Base_Init 2.2 中断模式启动定时器函数&#xff1a;HAL_TIM_Base_Start 2.3 定时器回调函数&#xff1a; HAL_TIM_PeriodElapsedCallback…
阅读更多...
信息系统项目管理师0128：输出（8项目整合管理—8.6管理项目知识—8.6.3输出）

信息系统项目管理师0128：输出（8项目整合管理—8.6管理项目知识—8.6.3输出）

点击查看专栏目录 文章目录 8.6.3 输出 8.6.3 输出 经验教训登记册 经验教训登记册可以包含执行情况的类别和详细的描述&#xff0c;还可包括与执行情况相关的影响、建议和行动方案。经验教训登记册可以记录遇到的挑战、问题、意识到的风险和机会以及其他适用的内容。经验教训…
阅读更多...
「云渲染课堂」3dmax地砖材质参数怎么让画面更加真实？

「云渲染课堂」3dmax地砖材质参数怎么让画面更加真实？

在3DMAX中&#xff0c;地砖材质的渲染需要细致的调整&#xff0c;因为不同材质的地砖在反射和折射参数上各不相同。为了使地砖材质更加逼真&#xff0c;以下简要说明了一些设置方法&#xff0c;希望对大家有所帮助&#xff01; 3dmax地砖材质参数如何设置 1、打开材质编辑器&a…
阅读更多...
C语言指针指针和数组笔试题（必看）

C语言指针指针和数组笔试题（必看）

前言&#xff1a; 前面介绍了指针的大体内容&#xff0c;如果接下来能够把这些代码的含义搞得清清楚楚&#xff0c;那么你就是代码king&#xff01; 一维数组&#xff1a; int a[] {1,2,3,4}; printf("%d\n",sizeof(a)); printf("%d\n",sizeof(a0)); pr…
阅读更多...
推荐系统学习笔记（三）

推荐系统学习笔记（三）

swing召回通道 Q&#xff1a;假如重合的用户是一个小圈子&#xff1a;在一个群里&#xff0c;毫无关联的笔记也会被同时交互 solve&#xff1a;降低小圈子权重--------------swing的主要目的------------给用户加权 相似度&#xff1a; a是人工参数&#xff0c;overlap降低小…
阅读更多...
基于Python+KNN神经网络手写数字识别

基于Python+KNN神经网络手写数字识别

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 手写数字识别是机器学习领域的一个基础问题&#xff0c;也是许多实际应用的基石&#xff0c;如邮政编码识别、银行表…
阅读更多...
STM32F1之SPI通信·软件SPI代码编写

STM32F1之SPI通信·软件SPI代码编写

目录 1. 简介 2. 硬件电路 移位示意图 3. SPI时序基本单元 3.1 起始条件 3.2 终止条件 3.3 交换一个字节&#xff08;模式0&#xff09; 3.4 交换一个字节&#xff08;模式1&#xff09; 3.5 交换一个字节&#xff08;模式2&#xff09; 3.6 交换一个字节&a…
阅读更多...
网络信息安全

网络信息安全

目录 引言 网络信息安全的基本概念 定义 主要目标 网络信息安全的范围 主要威胁 恶意软件 黑客攻击 拒绝服务攻击 社交工程 内部威胁 常用技术和防护措施 加密技术 防火墙 入侵检测和防御系统 访问控制 多因素认证 安全审计和监控 安全培训和意识提升 未来发…
阅读更多...
panic对defer语句的执行的影响

panic对defer语句的执行的影响

1.主线程中的panic会直接导致所有正在运行的go协程无法执行,还会导致声明在它之后的defer语句无法执行。 package mainimport ("fmt""time" )func main() {defer fmt.Println("defer1") //声明在panic之前的defer会执行go func() {defer fmt.Pri…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023