贪心算法--区间调度问题

贪心算法

引言

贪心算法是一种简单而有效的算法设计技巧，在解决一些优化问题时具有广泛的应用。其基本思想是通过每一步的局部最优选择，最终达到全局最优解。贪心算法通常不会回溯之前的决策，而是根据当前状态作出最优决策，因此其执行效率较高。

贪心算法的应用十分广泛，涵盖了诸多领域，如图论、计算机网络、调度问题等。在某些情况下，贪心算法能够给出最优解，但也存在一些问题并不适合贪心策略的情况。因此，了解贪心算法的原理、应用场景以及适用性是十分重要的。

原理

贪心算法（Greedy Algorithm）是一种解决问题的算法范式，其基本思想是通过每一步的局部最优选择，最终达到全局最优解。在贪心算法中，每一步都选择当前情况下的最优解，并希望通过这种局部最优的选择，最终得到全局最优解。

贪心算法的核心思想可以概括为以下两点：

贪心选择性质：贪心算法每一步都做出一个局部最优的选择，即当前情况下看起来最好的选择。
最优子结构性质：当一个问题的最优解包含其子问题的最优解时，称该问题具有最优子结构性质。贪心算法通过递归地求解子问题，并利用最优子结构性质，可以保证每一步的选择都是最优的。

贪心算法通常不会回溯之前的决策，而是根据当前状态作出最优决策。这使得贪心算法执行效率较高，但也限制了其能够解决的问题范围。贪心算法通常适用于满足贪心选择性质和最优子结构性质的问题，例如最小生成树、最短路径、任务调度等。

需要注意的是，并非所有问题都适合使用贪心算法求解，因为贪心算法可能会得到局部最优解而不是全局最优解。因此，在应用贪心算法时，需要仔细分析问题的特点，确保问题满足贪心选择性质和最优子结构性质，以及贪心算法能够得到正确的解。

应用场景

贪心算法在许多领域都有广泛的应用，特别是在以下几个方面：

最小生成树： 在图论中，贪心算法经常用于构建最小生成树，例如 Prim 算法和 Kruskal 算法。这些算法通过每次选择权值最小的边来构建最小生成树，从而实现图的最优连通。
最短路径问题： 在图论中，Dijkstra 算法和 A* 算法等都是基于贪心策略的最短路径算法。它们通过每次选择当前距离最短的顶点来逐步确定起点到其他顶点的最短路径。
任务调度问题： 在任务调度问题中，贪心算法可以用于优化任务的执行顺序，以使得总执行时间最小化。例如，按照任务的截止时间或处理时间进行排序，然后依次执行。
背包问题： 在背包问题中，贪心算法可以用于近似求解，例如分数背包问题中的分数贪心算法。这种算法每次选择单位价值最高的物品放入背包中，以尽可能达到背包的容量限制并使总价值最大化。
区间调度问题： 在区间调度问题中，贪心算法可以用于确定最大数量的互不重叠的区间。例如，会议安排问题中，每次选择结束时间最早的会议安排，以尽可能安排更多的会议。
Huffman 编码： Huffman 编码是一种用于数据压缩的贪心算法。它通过构建一棵最优前缀树来实现对字符的编码，使得出现频率较高的字符拥有较短的编码，从而实现数据的高效压缩。

实现贪心算法

本篇我们主要分享的是区间调度问题相关例题。

452. 用最少数量的箭引爆气球

我们以**[[10,16],[2,8],[1,6],[7,12]]**为例：

原气球的排列为：

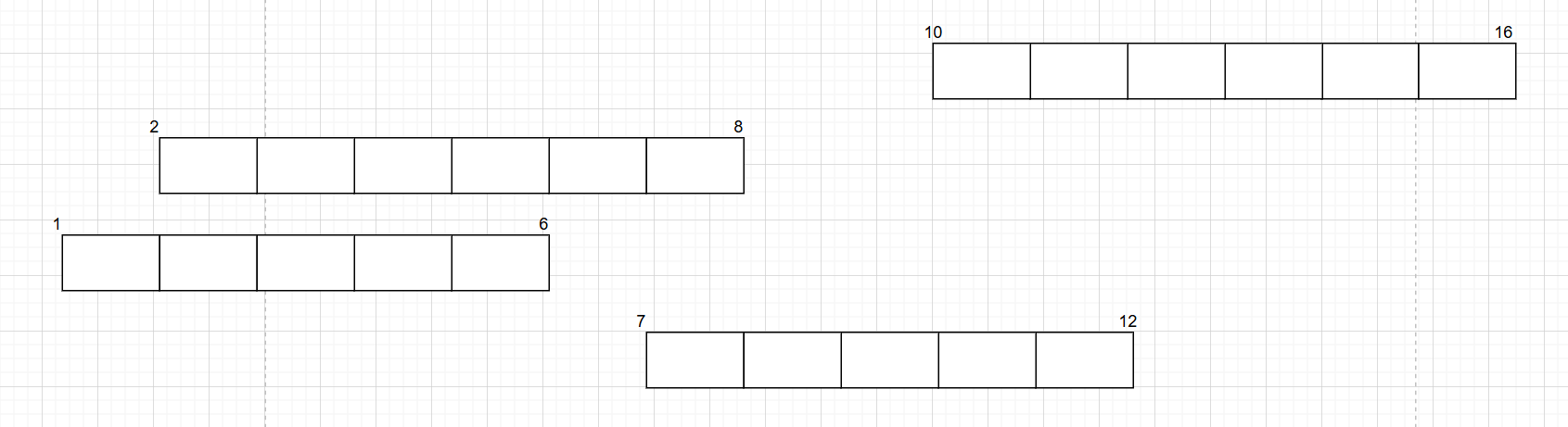
题目要求求出引爆所有气球所必须射出的最小弓箭数

如果按照原来顺序去判断的话，很难找出有重复的气球，所以我们可以对气球先进行排序（按照左边界或者右边界排序都可以，本题我按照左边界排序来进行讲解）

排序后为：

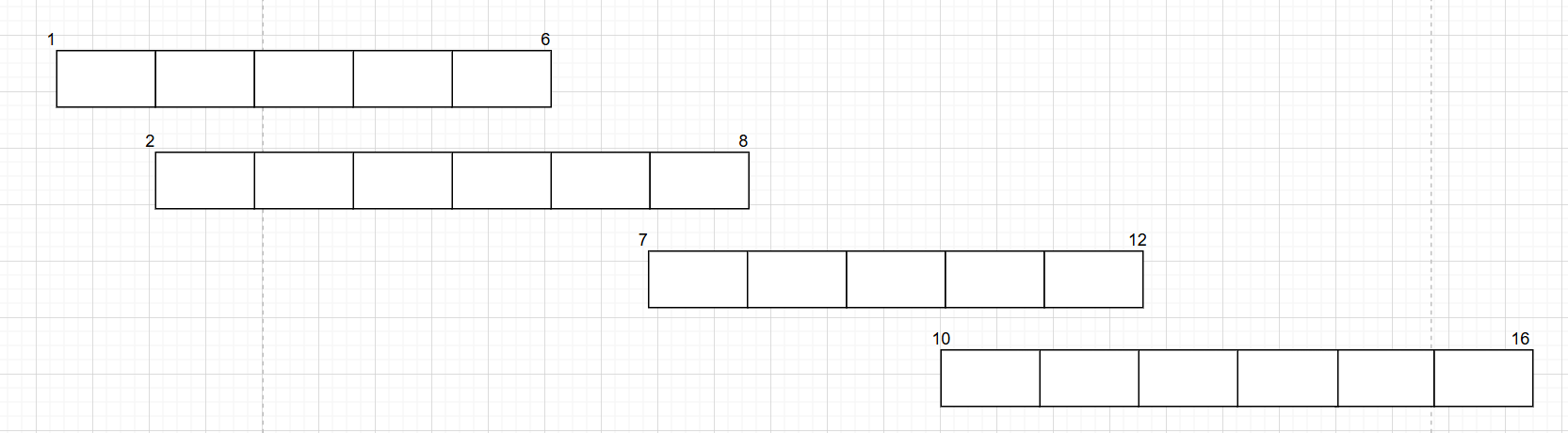
排序了之后我们就可以从上往下遍历去判断是否重合了。

当下面的气球的左边界小于等于上面气球的右边界时，证明两个气球重合，可以用一支箭引爆。

当然下面一个气球有可能和上面两个气球都重合，如果只和上面一个气球重合而不和上上面气球重合的话，那么还需要额外的一支箭去引爆。为了实现判断，当两支气球重合时，我们可以把右边界缩小为两个气球右边界较小的一个值（因为此时新气球的左边界一定大于等于上面两个气球的左边界，所以不用判断），如果新气球左边界小于上面气球的右边界，那么就不需要额外的箭就能引爆。

遍历完所有的气球，我们便可以统计出需要的箭的数量。

下面为代码实现：

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points.length == 0)
            return 0;
        Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));//不使用a[0] - b[0]而使用Integer.compare(a, b)是为了防止整数溢出
        int ans = 1;
        for (int i = 1; i < points.length; i++) {
            if (points[i][0] <= points[i - 1][1]) {
                points[i][1] = Math.min(points[i][1], points[i - 1][1]);//把上一个气球右边界修改为较小值
            } else {
                ans++;
            }
        }
        return ans;
    }
}

435. 无重叠区间

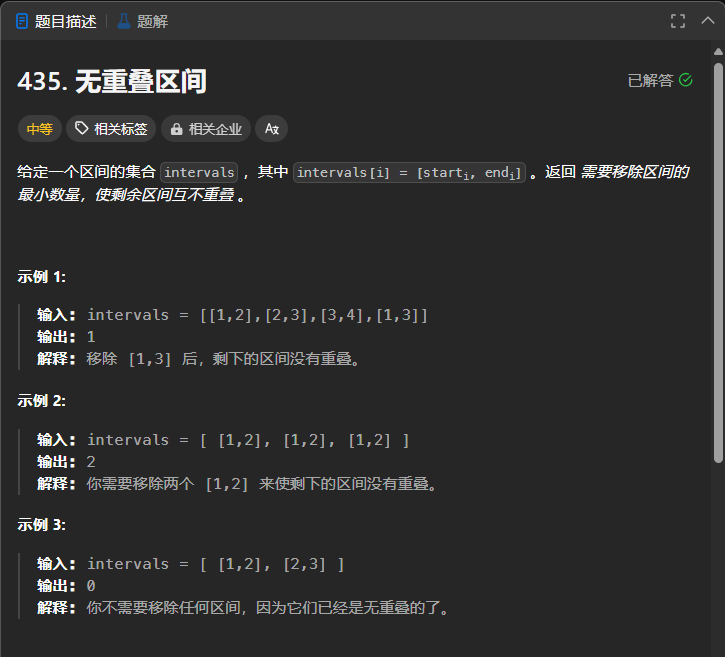
本题相比于上一题增加了一点难度，下面我是按照我的思路来讲解。

首先我们依然是要先进行排序（用**[[1,2],[2,3],[3,4],[1,3]]**举例）：

排序后为：

我们可以直观地看出只要删除1，3便可以实现剩下的区间没有重叠。

那么具体代码上怎么去实现呢？

整体思路和上一道题有些类似，当本区间左边界比上一个区间右边界小的时候我们就需要去删除了。删除在代码上只需要将此区间右边界设置为此区间与上一个区间中的较小值就可以了。如果此区间左边界大于等于上一个区间右边界，那么就证明两个区间没有重合，不需要进行操作。

下面是代码实现：

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        if (intervals.length == 0)
            return 0;
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
        int ans = 0;
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] < intervals[i - 1][1]) {
                intervals[i][1] = Math.min(intervals[i][1], intervals[i - 1][1]);
                ans++;
            } 
        }
        return ans;
    }
}

56. 合并区间

本题和上面两道题也比较类似，大致讲一下思路。

先进行排序，然后用此区间左边界与上一个区间右边界进行比较，如果满足重叠，则进行记录。

下面用代码来具体看一下：

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
        List<int[]> list = new LinkedList<>();
        for (int i = 0; i < intervals.length; i++) {
            if (list.isEmpty() || list.get(list.size() - 1)[1] < intervals[i][0]) {//如果集合为空或者此区间左边界大于最后录入集合的区间右边界，则直接记录答案就可以了，反之就证明有重叠
                list.add(intervals[i]);
            } else {
                list.get(list.size() - 1)[1] = Math.max(list.get(list.size() - 1)[1], intervals[i][1]);//重叠的区间左边界是不用变的，右边界需要修改成两个区间右边界的较大值，就可以了
            }
        }
        return list.toArray(new int[list.size()][]);
    }
}