Pytorch梯度下降算法（Gradient Descent）

news2024/10/5 14:59:22

intro

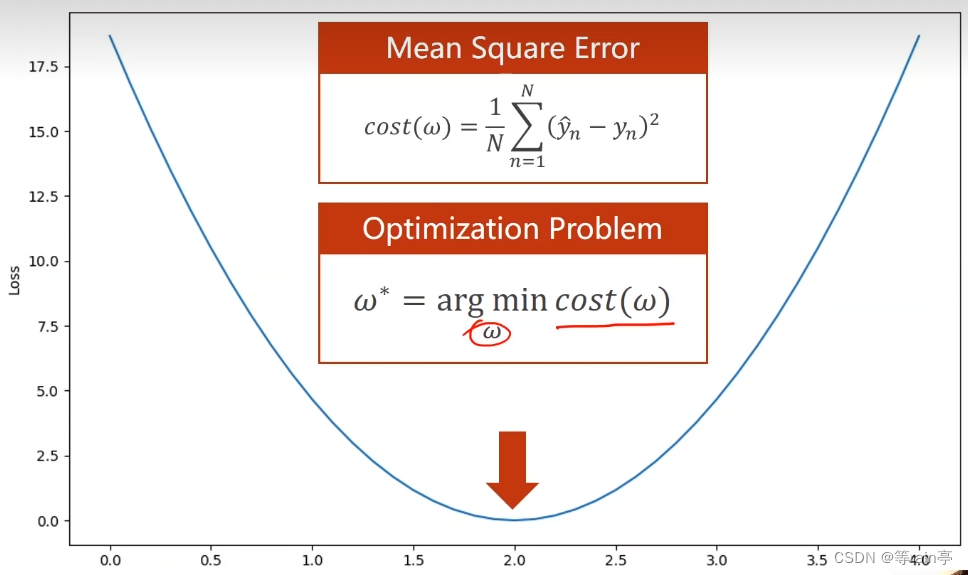其实对于我们将要学的梯度最小函数，目的就是先得到loss损失最小的值，然后根据这个最小的值去得到w。

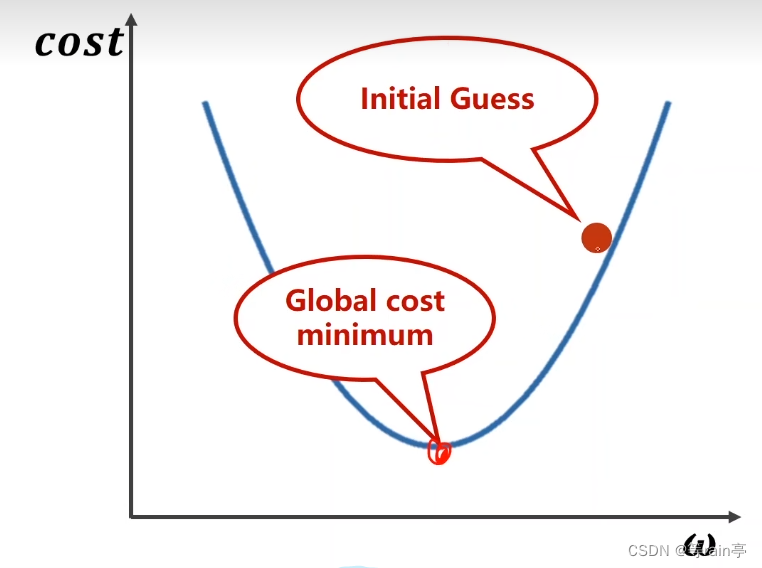初始点在initial guess这个位置，我们希望找到最小的权重点global cost minimum，我们到底是让这个点左移寻找还是右移寻找呢？

此时我们就需要使用到梯度定义。

在加上一个 $\Delta$ x后，如果这个导数值变为负的，说明我接下来函数图像呈现下降的趋势，那根据我们上述所说的寻找一个阶梯最小函数，就是要使函数往小的方向进行。所以我们希望函数图像下降的话，我们就取导数为负的方向。

因此我们可以每下降一部分可以更新一下权重。用来保留。公式中的a为学习率，学习率乘上这个导数表示我们每次大概在函数上走多远，通常来说学习率要小一点，但是也不能太小。

以上我们的梯度下降的算法，其实就是我们的贪心算法，它可能找不到全局最优解，但是可以找到局部最优解，大家可以思考一下为什么会出现这样的情况。大家可以看看下面的这个图，结合上面的介绍。

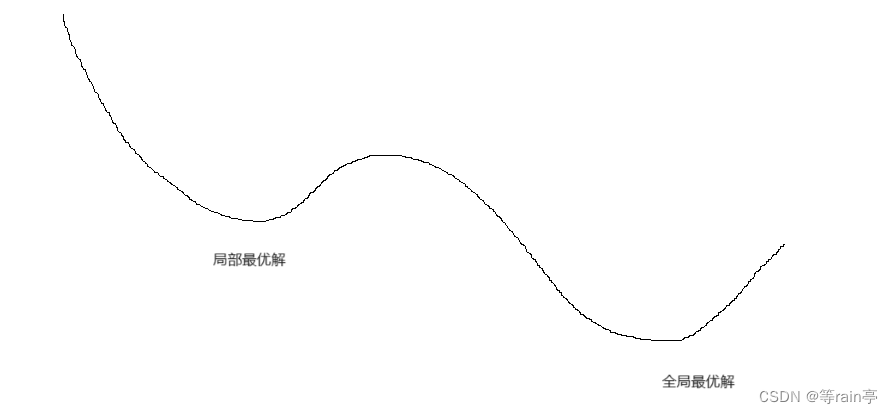
因为到局部最优点后，没有办法找到这个导数为负数的这样的情况了。

还存在一种点，鞍点。这个也可能无法到达全局最优点。鞍点就是出现了一个导数为0的线。

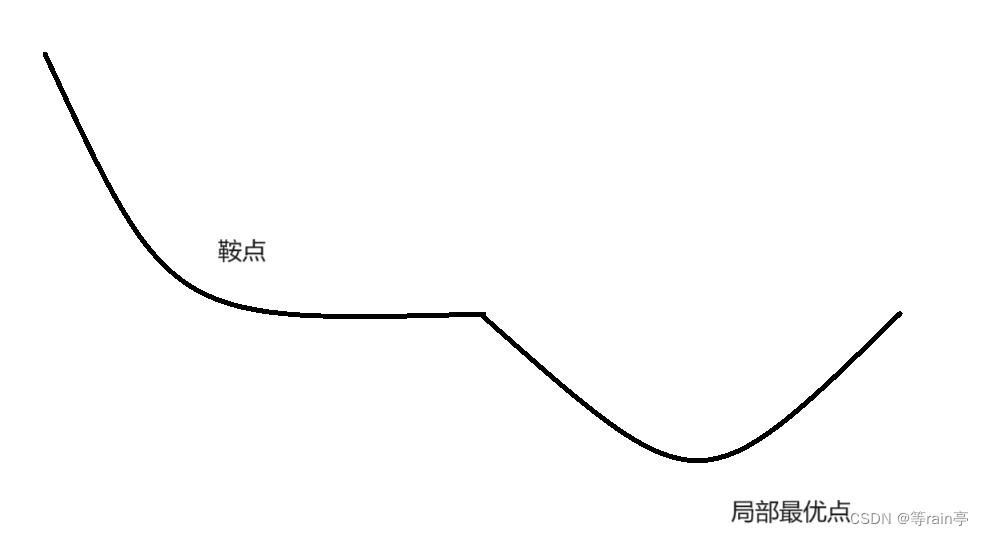
因为公式中 w=w-ag g为导数，此时导数为0了，w一直不变。

左边的式子是上一节中预测值y^减去真实值y（此时我们预测的y使用x*w)。此时求出的就是w权重值，对w进行求导，最终结合我们此次的内容，得到最后跟新出的w局部最优权重。

代码实现

x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
w=1.0

def forward(x):
    return x*w

def cost(xs,ys):
    cost=0
    for x,y in zip(xs,ys):
        y_pred=forward(x)
        cost+=(y_pred-y)**2
    return cost/len(xs)

def gradient(xs,ys):
    grad=0
    for x,y in zip(xs,ys):
        grad+=2*x*(x*w-y)
    return grad/len(xs)

print('Predict (before training)',4,forward(4))
for epoch in range(100):
    cost_val=cost(x_data,y_data)
    grad_val=gradient(x_data,y_data)
    w-=0.1*grad_val
    print('Epoch:',epoch,'w=',w,'loss',cost_val)
print('Predict (after train)',4,forward(4))

随机梯度下降

在深度学习中，使用梯度下降还是比较少的，通常我们使用的是随机梯度下降（Stochsstic gradient descent）。

我们可以看出，我们梯度下降使用的是使用整个损失的平均损失作为梯度下降的依据，但是随机梯度下降变成了单个样本的损失函数来进行更新。使用这个随机梯度时，由于每一个点都会存在噪声，那即使我们陷入了鞍点，噪声也会推动我们向前运动。

在更新的过程中会跨出鞍点，往后面进行运动。

代码修改

#原先的cost 现在变成loss 现在不用求均值了
def loss(x,y):
    y_pred=forward(x)
    return (y_pred-y)*2

#原先的gradient也不需要求均值了
def gradient(x,y):
    return 2*x*(x*w-y)

for epoch in range(100):
    for x,y in zip (x_data,y_data):
        grad=gradient(x,y)
        w=w-0.1*grad_val #此时的w也不用去累积计算了
        print('\tgrad:',x,y,grad)
        l=loss(x,y)
    print('progress:',epoch,'w=',w,'loss:',l)

大家可以看上述代码和梯度下降算法的差距，几乎都是将在梯度下降算法中的每一个求均值的部分都修改成求一次。

但是出现一个问题：

对于一个梯度下降算法，其实我们在使用模型计算时不管是对x1还是（x+1）求解f（x）时，两者是没有依赖关系的，这些运算可以并行。但是使用随机梯度下降时，每次都会更新，两者存在依赖关系。所以说梯度下降算法的时间复杂度是优于随机梯度下降算法的。