参考书籍：《机器人学导论》John.J.Craig

机器人方面的学习和线性代数、矩阵论部分的学习密切相关，建议先学习线性代数会更好理解此部分内容。虽然学了线代但是能忘的都忘得差不多的我要泪目了。本文主要介绍基础的运动学和动力学区别，正向运动学、逆向运动学的简单介绍。

写在前面：推荐书籍和教学视频

机器人学习书籍推荐 - 知乎基础篇机器人与数学（尤其是微积分、线性代数、矩阵论、概率论、数值方法等）之间有着密切的关系。因此，为了能够更好理解诸如刚体的位姿描述与变换，正逆运动学 / 动力学、微分运动学等知识，建议首先打好数学基…https://zhuanlan.zhihu.com/p/144466970

 目录

一、区分运动学和动力学

1.1运动学 (Kinematics)

1.2动力学 (Dynamics)

1.3主要区别

1.4其他力学

材料力学（Mechanics of Materials）

系统动力学（System Dynamics）

二、运动学-正向逆向

正向运动学 (Forward Kinematics)

应用和过程：

应用实例：

逆向运动学 (Inverse Kinematics)

应用和过程：

应用实例：

比较

实例说明

正向运动学实例：

逆向运动学实例：

---

一、区分运动学和动力学

一字之差，研究的东西有比较大的差异。简而言之，运动学是描述“物体如何运动”的科学，而动力学是解释“为什么物体会这样运动”的科学。

运动学（Kinematics）和动力学（Dynamics）是力学的两个重要分支，尽管它们都涉及物体的运动，但研究的侧重点不同。

1.1运动学 (Kinematics)

运动学主要研究物体运动的几何特征，而不考虑引起这种运动的力和质量。运动学主要回答“如何运动”的问题，而不涉及“为什么会运动”。研究内容包括：

1. 位置（Position）：物体在空间中的具体位置。

2. 速度（Velocity）：物体位置随时间变化的快慢和方向。

3. 加速度（Acceleration）：物体速度随时间变化的快慢和方向。

运动学的基本方程主要通过位置、速度和加速度的关系来描述物体的运动轨迹和运动规律。

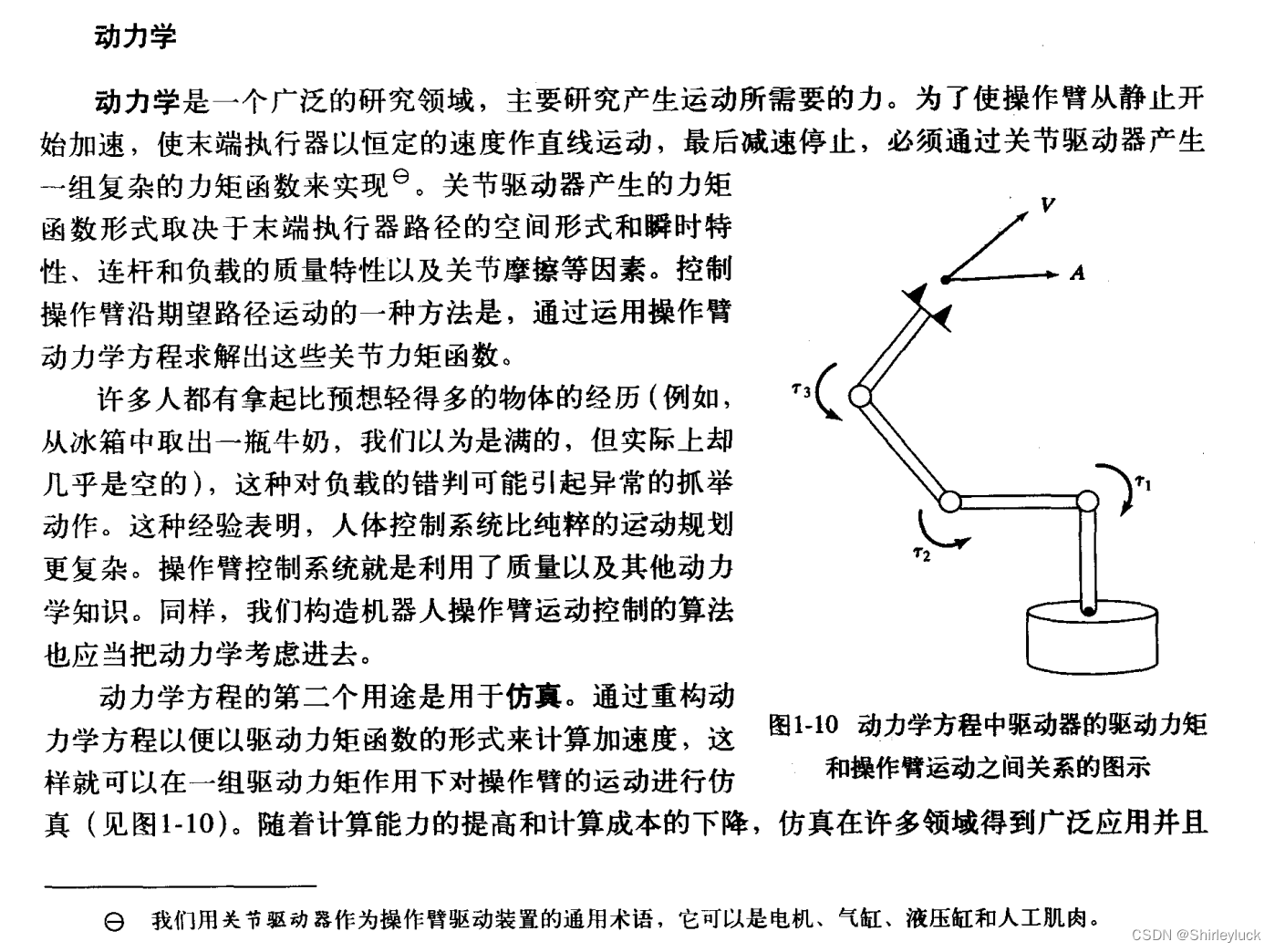
1.2动力学 (Dynamics)

动力学研究引起物体运动的原因，即力和物体的质量。它不仅描述物体如何运动，还解释为什么物体会这样运动。动力学包括以下两个主要分支：

1. 质点动力学（Particle Dynamics）：研究质点或质点系的运动。通过牛顿运动定律，分析质点在各种力作用下的运动。

2. 刚体动力学（Rigid Body Dynamics）：研究刚体的运动，考虑刚体的质量分布和力矩。

动力学的基本方程主要包括牛顿第二定律（\(F = ma\)）和动量守恒定律等，用来描述力如何作用于物体并引起其运动。

1.3主要区别

1. 研究对象

   - 运动学：研究物体的运动规律，主要关注位置、速度和加速度等物理量的变化。

   - 动力学：研究物体的运动原因，主要关注力、质量以及它们如何影响物体的运动。

2. 是否考虑力：

   - 运动学：不考虑作用在物体上的力。

   - 动力学：考虑作用在物体上的力及其对运动的影响。

3. 方程和描述：

   - 运动学：使用运动方程描述位置、速度和加速度之间的关系。

   - 动力学：使用牛顿运动定律和其他力学定律描述力和运动的关系。

1.4其他力学

材料力学（Mechanics of Materials）

材料力学是研究材料在外力作用下的变形和内部应力分布的学科。主要内容包括：

1. 变形（Deformation）：研究材料在外力作用下的形变，通常使用应变（Strain）来描述。这包括拉伸、压缩、剪切和弯曲等不同类型的变形。
2. 应力（Stress）：研究材料内部由于外力作用产生的力。应力通常以力除以面积表示，有正应力（拉伸或压缩）和剪应力。
3. 微元（微分单元）：在材料力学中，通过微分单元（即微元）的概念，分析材料内部应力和应变的分布。微元分析帮助理解材料在不同点上的受力和变形情况。
4. 弹性和塑性：研究材料在不同载荷下的响应，包括弹性变形（可恢复的）和塑性变形（不可恢复的）。
5. 材料的性质：包括杨氏模量（Elastic Modulus）、屈服强度（Yield Strength）、断裂韧性（Fracture Toughness）等参数。

系统动力学（System Dynamics）

系统动力学是一门研究复杂系统的行为及其相互作用的学科。它广泛应用于工程、物理、生物、经济和社会科学等领域。以下是一些核心概念：

1. 阻尼（Damping）：阻尼是指系统中由于摩擦或其他阻力导致能量耗散的现象。在动力学系统中，阻尼影响系统的振动特性和稳定性。常见的阻尼类型包括粘性阻尼（Viscous Damping）和库仑阻尼（Coulomb Damping）。
2. 自由度（Degrees of Freedom）：系统中独立运动的数目。自由度越多，系统的动态行为越复杂。
3. 振动分析：研究系统在外力作用下的振动响应，包括固有频率、模态分析和谐振现象。
4. 微分方程：动力学系统通常通过微分方程描述其时间演变行为，包括牛顿方程、拉格朗日方程和哈密顿方程等。
5. 反馈和控制：研究系统如何通过反馈机制进行控制，以达到稳定或期望的行为。

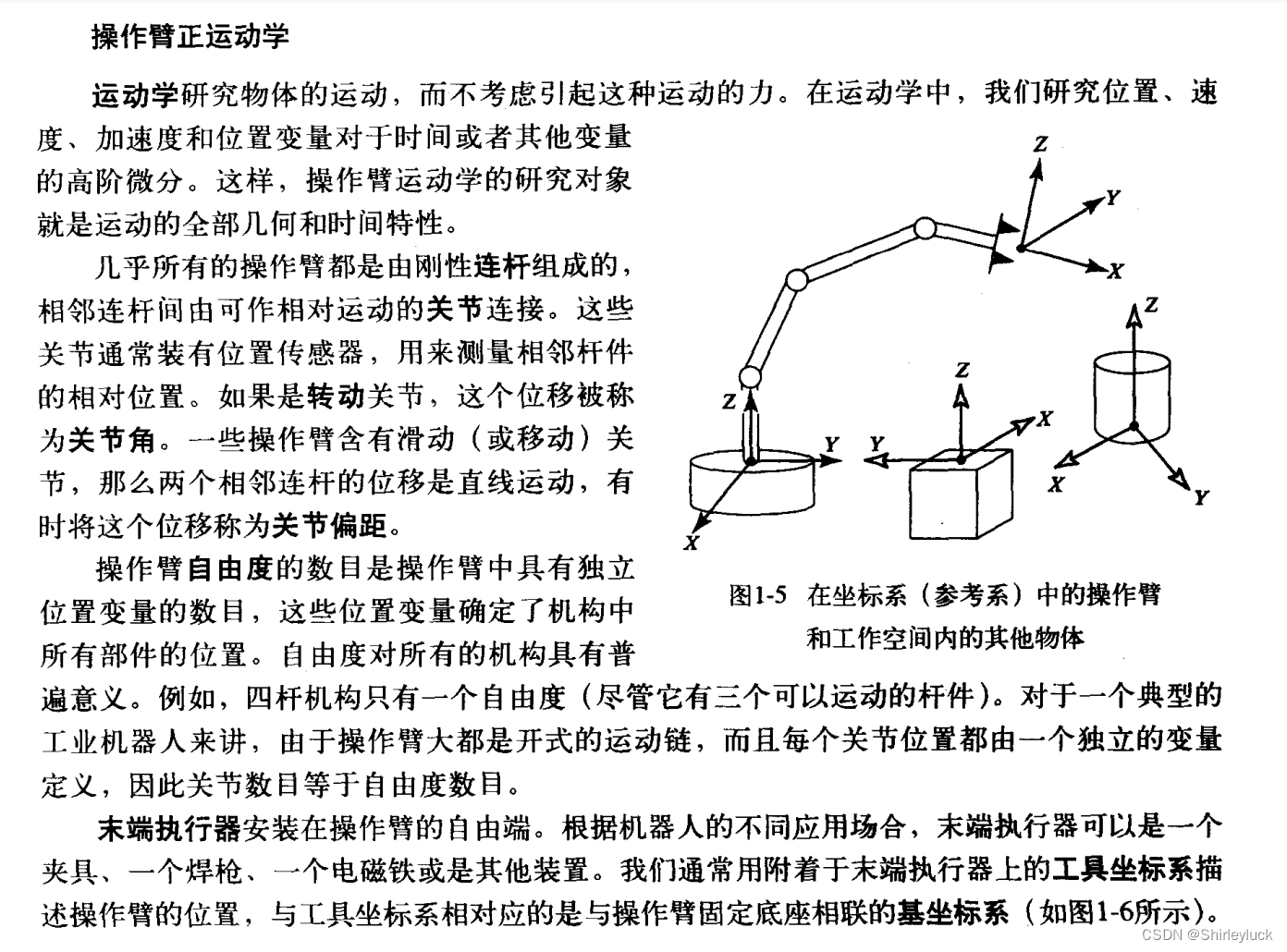
二、运动学-正向逆向

正向运动学（Forward Kinematics）和逆向运动学（Inverse Kinematics）是运动学中两个重要的概念，特别是在机器人学、计算机图形学和动画中应用广泛。它们分别解决不同的问题：

正向运动学 (Forward Kinematics)

正向运动学研究的是从机器人的关节参数（如角度、位置）推导出末端执行器的位置和姿态的问题。也就是说，给定各个关节的运动状态，计算机器人末端的具体位置和方向。

应用和过程：

1. 输入：关节的角度或位置。
2. 输出：末端执行器的位置和姿态（例如在三维空间中的位置和方向）。
3. 过程：使用几何关系和转换矩阵，通过逐层变换计算出最终的位置信息。

正向运动学主要使用的是关节空间到工作空间的转换。具体方法包括使用齐次变换矩阵、旋转矩阵和位移向量等。

应用实例：

• 机器人手臂：确定机器人手臂的每个关节角度，计算手臂末端的位置以执行特定任务。
• 动画制作：计算一个角色骨骼的各部分位置，使角色摆出预定的姿势。

逆向运动学 (Inverse Kinematics)

逆向运动学研究的是从末端执行器的位置和姿态推导出需要的关节参数的问题。即给定末端执行器的目标位置和方向，求解各个关节的角度或位置。

应用和过程：

1. 输入：末端执行器的目标位置和姿态。
2. 输出：各个关节的角度或位置。
3. 过程：通过逆向计算，求解出能够实现末端执行器到达指定位置的关节参数。

逆向运动学是工作空间到关节空间的转换。求解逆向运动学问题通常比正向运动学更复杂，可能需要使用数值方法、优化算法或迭代求解技术。

应用实例：

• 机器人手臂：确定机器人手臂末端需要到达某一位置，通过计算得出各个关节的角度。
• 虚拟角色动画：通过控制角色的手、脚等末端位置，计算角色的关节角度来生成自然的动作。

比较

• 难度：

  • 正向运动学：计算较为直接，通常通过直接的几何关系或矩阵变换即可求得结果。
  • 逆向运动学：计算较为复杂，涉及求解非线性方程组，有时可能有多解或无解的情况。

• 应用领域：

  • 正向运动学：主要用于模拟和分析给定关节参数下的运动情况，常见于运动规划和路径生成。
  • 逆向运动学：主要用于目标驱动的运动控制，例如让机器人手臂抓取特定物体，或让虚拟角色摆出特定姿势。

实例说明

简单例子去理解一下，以后的篇幅会细写怎么进行运动学的正解逆解。

正向运动学实例：

设有一个两连杆机械臂，关节角度分别为 𝜃1 和 𝜃2，连杆长度分别为 𝐿1和 𝐿2。末端执行器的位置 (𝑥,𝑦)可以通过正向运动学计算为：

逆向运动学实例：

对同一个两连杆机械臂，若末端执行器需要到达位置 (𝑥,𝑦)，逆向运动学求解各个关节角度 𝜃1和 𝜃2。方程组可能是：

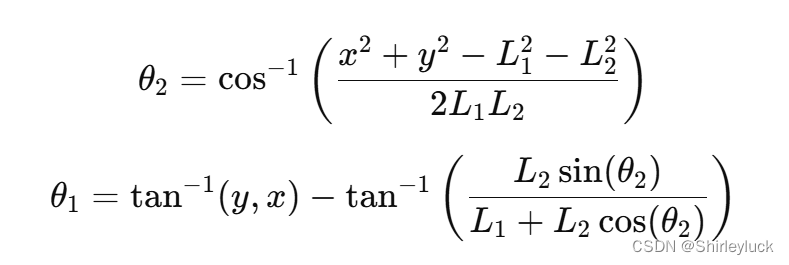
通过这些方程，可以求出机器人关节的角度，以实现末端执行器到达指定位置的目标。