一、学过的排序

1.插入排序 2.希尔排序

3.直接选择排序 4.堆排序

5.冒泡排序 6.快速排序

7.归并排序 8.计数排序

二、各项排序的思想及改进(无特殊说明均以升序为例)

1.插入排序及其改进希尔排序

（1）插入排序的思想及具体操作细节

          将一个数字按顺序插入已排好序的数组，插入会涉及移动已排好序的部分。将数组中的每一个数与其之前的每一个数逐一比较，同时后移不比插入数据小的数，直到遇到比其小的，再插入在那个数后。

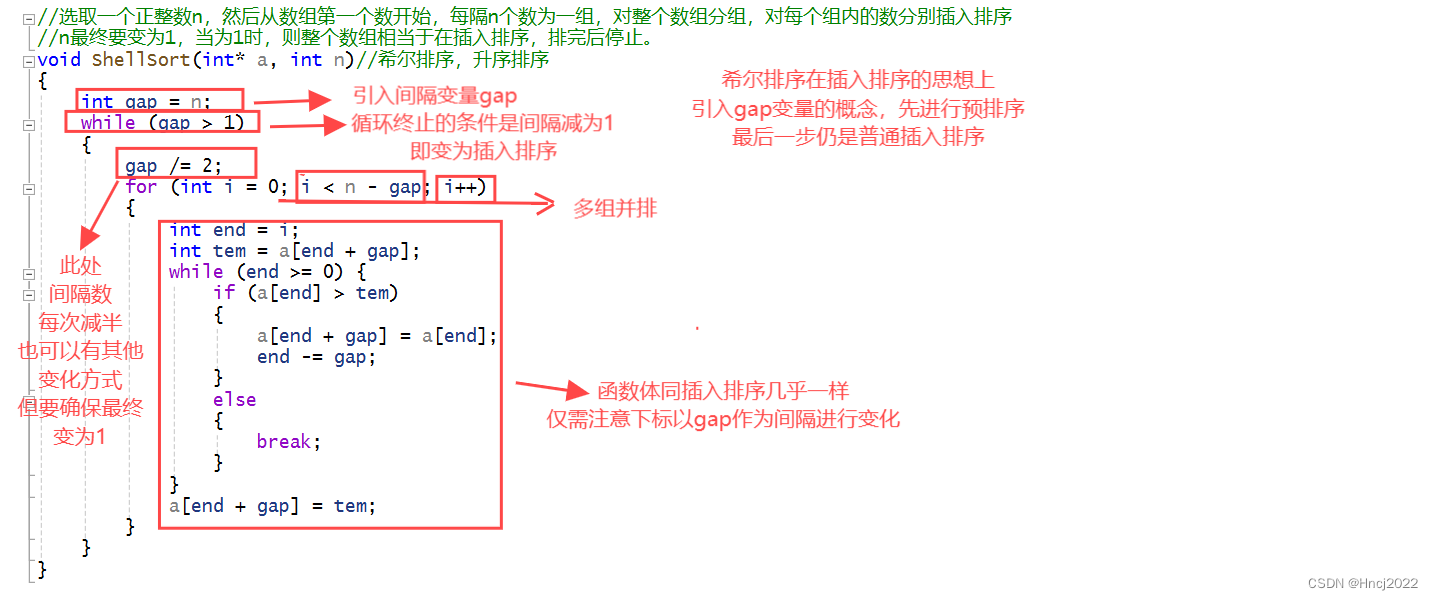
  (2)希尔排序的思想及具体操作细节

         在插入排序排序的基础上先每gap个数分为一组进行插入排序，最后gap变为1对整个进行过分组的数组进行普通插入排序，由于已进行过分组插入排序的预排序处理，最后的插入排序效率会变高。希尔排序函数体几乎与插入排序一致

          

2.直接选择排序与堆排序

  (1)直接选择排序的思想及具体操作细节

   选择排序性能差，不常用。运用双指针思想，不断缩小排序范围，一次排序中去找当前排序范围中的最大与最小值，最大值放右边，最小值放左边，不断循环直至左右指针相遇。注意当左边界指向当前范围最大值后，原来的最小值位置存储了当前的最大值，所以右边界应与最小值位置交换

   

(2) 堆排序的思想与具体操作细节

   建堆，排升序建大堆，降序减小堆。建议使用向下调整建堆，比向上调整建堆效率高。建堆需要依靠父节点算子节点，也需要依靠子节点算父节点。大根堆是子节点比父节点小，小根堆是父节点比子节点小。

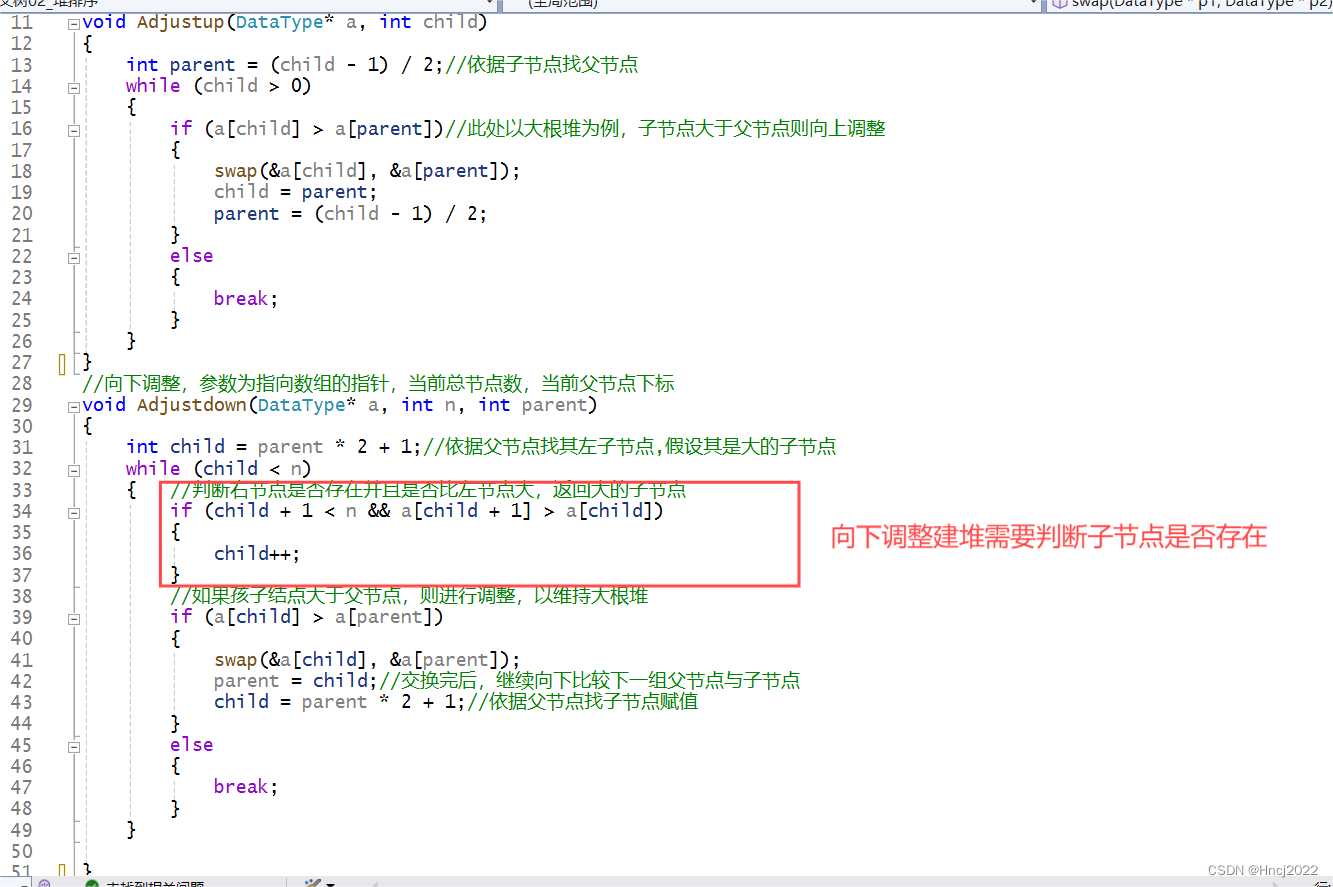
堆排序需要先根据升降序要求建堆，再对堆进行调整

 3.冒泡排序与快速排序及其改进

    (1)冒泡排序的思想及具体操作细节

       双重循环即可实现冒泡排序

(2)快速排序的思想及具体操作细节

 快速排序的每次排序其实只将数组中的一个数放置到了正确位置，该数被称为关键字，且以后的排序都不需要再移动该关键字，而是以关键字为分割线，将数组分为两部分，运用递归的方式对两部分重复上述操作，直至所有数排到正确位置上。所以一次排序后关键字的处理很重要，下述所有快排方法的每一次排序结束均与关键字的返回，此时还引出另一个问题，关键字该如何选取。

最初关键字都是选取当前排序范围最左边的数，然后从排序范围内的左边找比关键字第一个大的数字，从右边找比关键字小的第一个数字（注意此处是以排升序为例，应让用右边先动），让这两个交换位置，若左右指针未相遇，则继续重复该过程，最后所有比关键字小的排在关键字左边，比关键字的大的排在关键字右边。 在这之后再交换此时左指针指向的数和关键字，使得关键字位于中间。

关键字还可以通过随机数选取，但选出来后，仍然要放到排序范围的最左边，后续操作同上。仅需将选关键字并界定边界的部分替换成如下代码

 

关键字还可以三数取中法选取，但选出来后，仍然要放到排序范围的最左边，后续操作同上。

 

 

上述均为关键词选取的改进，从数据交换的角度还可以用挖坑法改进，其本质同上述代码并没有改变，只是在交换数据以进行排序时不再需要调用Swap()交换函数而是直接交换

上述算法本质均是通过左右指针，在一轮循环中让数组中的一个数排到其正确的位置，还可以通过前后指针法的思想，将小的数前移，大的数后推实现升序。注意该方法不是一次性就可以排好整个数组，仍是一次排好一个数，然后通过递归排好整个数组。  改种方法仍沿用递归的方式 ，但减少了每次排序的循环，且相比之前需要操控左右指针更好实现。

其实上述方法的递归流程图类似于二叉树，递归需要不断建立栈帧，深度过深时需要的空间会比较大 ，其实数据个数在小于一定程度后（此处假定数据量小于10），换用插入排序会在不影响效率的情况下节省空间。这被称为小区间优化

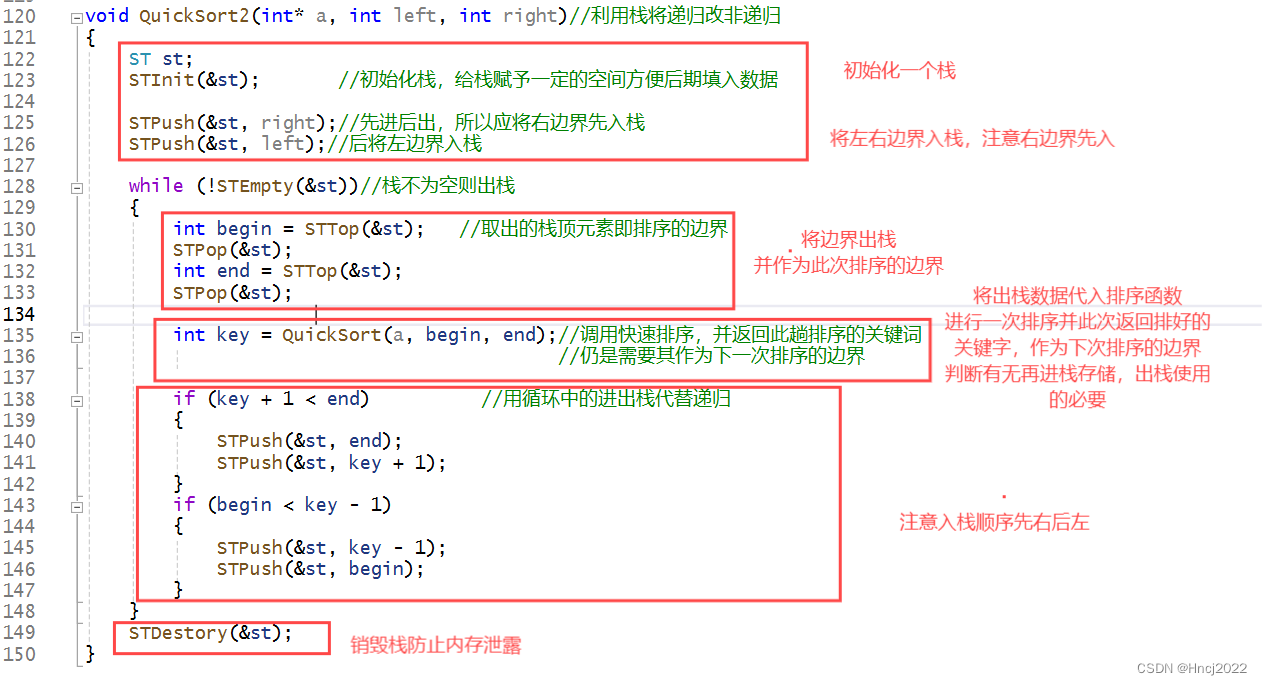
除了递归，应会改非递归   ，通过栈可将快排改为非递归，栈有先进后出的性质，向栈中按正确顺序压入边界值，再通过调用快排函数，完成排序后返回新的边界，再将新的边界压入栈，循环往复这个过程，可以替代递归调用。

4.归并排序的思想及其具体操作细节

  (1)递归的归并思想

       先对待排序的数组不断的以中线划分成两组，递归的进行划分，直至每组中只有一个数为止，该部分操作是分解，在这之后用分治的思想，分别对分解出来的几组数组从第一个元素开始进行比较，按照从小到大的顺序，两组两组的将已有序的数据合并，放入预先申请的动态区间中，最后用内存复制函数，将排好序的数据复制回原数组，覆盖原来无序的数据。 

(2)循环将递归改为非递归

  5.计数排序的思想及具体操作细节

数组的下标从0开始记，一直是从小到大连续变化且有序的，如果可以将需要排序的数字直接或间接当作数组中的下标，那么待排序的数字就有序了。此处需要统计待排序的数据中的每个数字的个数，然后依次朝数组中有几个放几个。

  

      

三、各种排序的性能及稳定性分析

排序算法的性能分析通常基于时间复杂度、空间复杂度、稳定性以及适应性等方面。以下是一些常见排序算法的性能分析：

1. **冒泡排序（Bubble Sort）**

    * 时间复杂度：O(n^2)，其中n是待排序元素的数量。冒泡排序在最好和最坏的情况下都有相同的时间复杂度。
    * 空间复杂度：O(1)，冒泡排序是一个原地排序算法，不需要额外的存储空间。
    * 稳定性：稳定
    * 适应性：对于已经部分排序的数据，冒泡排序的性能不佳。

2. **选择排序（Selection Sort）

    * 时间复杂度：O(n^2)，选择排序在最好和最坏的情况下都有相同的时间复杂度。
    * 空间复杂度：O(1)，选择排序也是一个原地排序算法。
    * 稳定性：不稳定
    * 适应性：与冒泡排序相似，选择排序在处理已部分排序的数据时性能不佳。

3. **插入排序（Insertion Sort）**

    * 时间复杂度：O(n^2) 在最坏的情况下，O(n) 在最好的情况下（当输入数组已经排序时）。
    * 空间复杂度：O(1)，插入排序是原地排序。
    * 稳定性：稳定
    * 适应性：对于小数据集或部分已排序的数据集，插入排序通常比其他O(n^2)算法（如冒泡排序和选择排序）更快。

4.**希尔排序**

1. **时间复杂度**：在最佳情况下，时间复杂度可以达到O(n)，但最坏情况下仍可能为O(n^2)。希尔排序的性能很大程度上取决于增量序列的选取，不同的增量序列会导致不同的排序效果。常用的增量序列有N/2、Hibbard序列（Dk=2^k-1）等。

2. **空间复杂度**：希尔排序的空间复杂度为O(1)，因为它是一个原地排序算法，不需要额外的存储空间。

3. **稳定性**：希尔排序是不稳定的排序算法。由于它采用分组和组内插入排序的方式，当相同关键字的记录被划分到不同的子表时，可能会改变它们之间的相对次序。

4. **适应性**：希尔排序算法仅适用于线性表为顺序存储的情况。它对于中等规模的数据集可能表现出较好的性能，但在处理大型数据集时，可能不如一些更高效的排序算法（如快速排序、归并排序等）表现得好。

4. **归并排序（Merge Sort）**

    * 时间复杂度：O(n log n)，归并排序的时间复杂度始终相同，无论输入数据的初始状态如何。
    * 空间复杂度：O(n)，归并排序需要额外的存储空间来合并子数组。
    * 稳定性：稳定
    * 适应性：归并排序是一种分治算法，适用于大型数据集。

5. **快速排序（Quick Sort）**

    * 时间复杂度：平均情况下为O(n log n)，最坏情况下为O(n^2)。快速排序的性能取决于所选的基准元素。
    * 空间复杂度：O(log n) 在平均和最好情况下，O(n) 在最坏的情况下，这是由于递归调用栈所需的空间。然而，可以使用迭代方法减少空间复杂度到O(1)。
    * 稳定性：不稳定
    * 适应性：快速排序是一种高效的排序算法，特别适用于大型数据集。

6. **堆排序（Heap Sort）**

    * 时间复杂度：O(n log n)，堆排序的时间复杂度始终相同，与输入数据的初始状态无关。
    * 空间复杂度：O(1)，堆排序是原地排序，但需要额外的空间来维护堆结构（通常通过索引或指针实现）。
    * 稳定性：不稳定
    * 适应性：堆排序适用于大型数据集，并且在构建堆的过程中可以方便地找到最大或最小元素。

在选择排序算法时，需要根据具体的应用场景和需求来权衡各种因素。例如，对于小型数据集或需要稳定排序的情况，插入排序或冒泡排序可能是合适的选择；而对于大型数据集，归并排序、快速排序或堆排序可能更为高效。