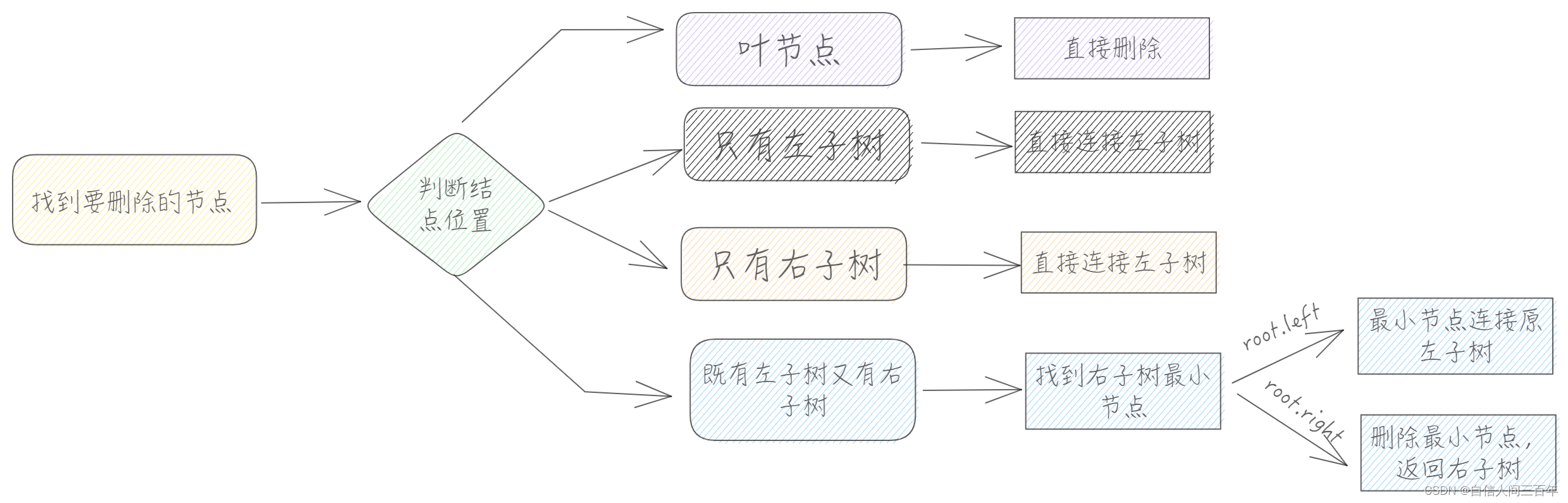
二叉树节点删除的几种情况

今天我们研究一下二叉搜索树(BST)的删除操作。删除操作对树来讲有些复杂，包含以下场景：

1. 删除点是叶节点
2. 删除点非叶节点，只有左子树
3. 删除点非叶节点，只有右子树
4. 删除点非叶节点，既有左子树又有右子树

基本步骤

Java代码的实现过程

第一步:查找要删除的值

如果找到值

 public TreeNode<Integer> delNode(TreeNode<Integer> root, T val){
    if(root.data.compareTo(val) == 0 ){ //查找到要删除的值
        
    }          
 :

当找到要删除的节点时，有四种情况需要考虑

1. 情况一：如果为叶节点，则删除叶节点，即返回null，断开与其父节点的引用

 if (root.left == null && root.right == null) {
                return null;
  }

2. 情况二：如果其左节点为null，右节点不为null

 if (root.left == null) {
                return root.right;
  }

3. 情况三：

 if (root.right == null) {
                return root.right;
  }

4. 情况四（重点）:

使用Hibbard Deletion 的二叉树删除方法
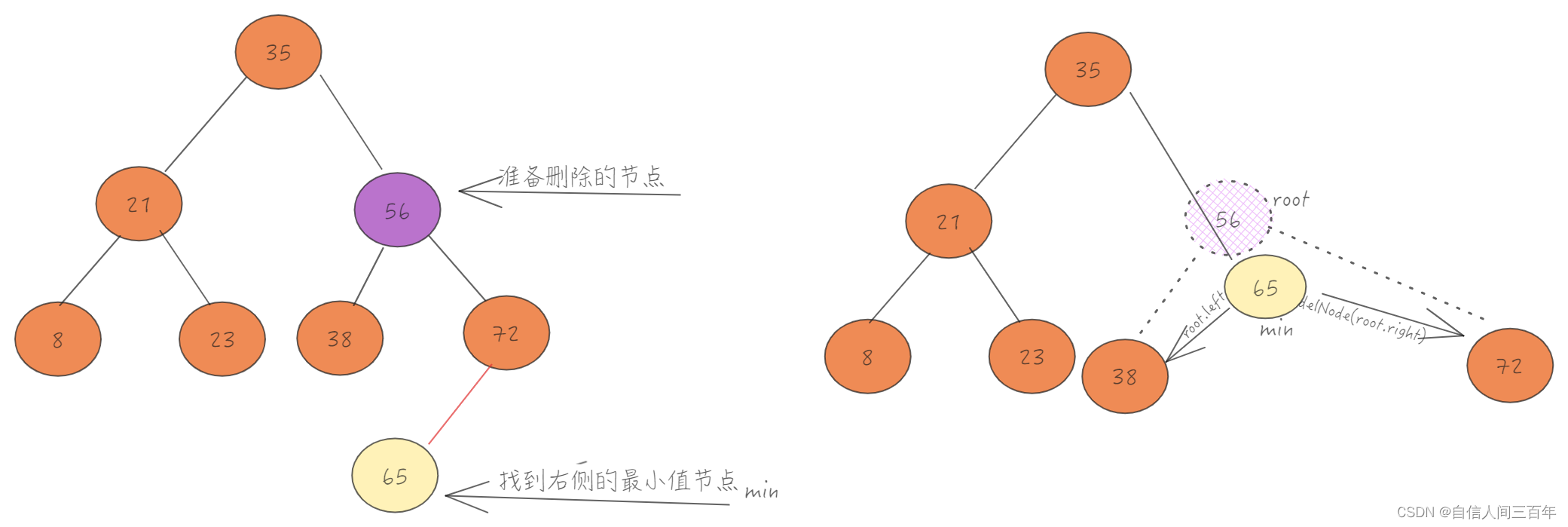
如图所示找到右子树的最小值，将最小值节点替换为删除节点的位置。最小值节点在连接原来节点的左、右子树。连接右子树时删除原来的最小值节点。

第一步

找到要替换的右子树最小值(65),即右子树中的最左节点（左小右大)。

public TreeNode<T> minNode(TreeNode<T> root) {
    while (root.left != null) {
        root = root.left;
    }
    return root;
}
 TreeNode<T> min = minNode(root.right);

第二步

最小节点连接右侧，再连接左侧。

连接右子树

访问要删除节点（56）的右子树，删除最小节点，返回（56）的右子树。

最小节点连接右子树

 min.right = delNode(root.right,min.data);

连接左子树

最小节点连接左子树

 min.left  = root.left;

回收当前节点

即删除当前节点，返回新的节点引用

return min;

完整代码

public TreeNode<T> delNode(TreeNode<T> root, T val) {
    if (val.compareTo(root.data) == 0) { //找到节点值相等
        //1. 要删除的节点是叶节点
        if (root.left == null && root.right == null) {
            return null;
        }
        //2. 要删除的节点的左节点为空,右节点不为空
        if (root.left == null) {
            return root.right;
        }
        //3.要删除节点的右节点为空
        if (root.right == null) {
            return root.left;
        }
        /*
         * 当前节点的左右节点都不为空,
         * 找到最小节点
         */
        TreeNode<T> min = minNode(root.right);
        min.right = delNode(root.right,min.data);
        min.left  = root.left;

        return min;


    } else if (val.compareTo(root.data) < 0) { //比当前节点值小,递归查找左子树
        root.left = delNode(root.left, val);
    } else { //比当前节点值大,递归查找右子树
        root.right = delNode(root.right, val);
    }
    return root;
}

public TreeNode<T> minNode(TreeNode<T> root) {
    while (root.left != null) {
        root = root.left;
    }
    return root;
}

如果当前值小于节点的值

else if(val.compareTo(root.data) < 0){
	root.left = delNode(root.left, val);
}

如果当前值大于节点的值

else{ //比当前节点值大
	root.right = delNode(root.right, val);
}