✨✨✨专栏：排序算法 

          🧑‍🎓个人主页：SWsunlight

目录

​编辑

前言：

一、堆排序：

时间复杂度：

空间复杂度：

算法稳定性：

二、升序的实现：通过建大堆实现

>思路：

1、向上调整算法实现大堆的建立：了解即可

 2、向下调整算法实现大堆的建立：

 3、排序：

 代码实现升序：

三、降序的实现：通过建小堆实现

>思路：

1、向上调整算法实现小堆的建立：了解即可

​编辑

2、向下调整算法实现小堆的建立：

​编辑

3、排序：

代码：

四、建堆的时间复杂度计算：

五、总结：

---

---

前言：

        本文基于对堆已经理解并通过代码实现后进行的，不知道堆的可以看上篇文章：堆

一、堆排序：

概念：   堆排序(Heapsort)是指利用 堆 这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

利用了堆的特点：堆分为大根堆和小根堆，是完全二叉树。为啥升序大堆，降序小堆：大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。相反小堆最小值一定在堆顶；

时间复杂度：

        堆排序包括构建堆和排序两个操作：
        构建堆的时间复杂度：              T(n) = O(n)
        排序过程的时间复杂度：         ​​​​  T(n) = O(nlog2n)
        堆排序整体的时间复杂度：       T(n) = O(nlog2n)

空间复杂度：

         O(1)     实现排序不需要额外的空间，就是以数组自身的空间进行的

算法稳定性：

           堆的调整过程中，值相同的结点在比较过程中不能保证顺序，所以堆排序是一种不稳定的排序方法

二、升序的实现：通过建大堆实现

>思路：

1. 将待排序数组构造成一个大堆
2. 这个序列最大值在堆顶
3. 将其与末尾元素进行交换，末尾变成最大值
4. 将剩下的n-1个结点重新调整为大堆
5. 再次将最大值与新的末尾元素（此时有n-1个结点）交换
6. 重复下去，到最后就是有序的了，整个数组最小的元素此时在栈顶

1、向上调整算法实现大堆的建立：了解即可

我们将上图数组的第一个元素作为堆顶（即下标为0的元素），进行建堆，然后将第二个数据看成是插入堆（会进行比较，谁大谁会放到堆顶），依次类推，直到数组的最后一个元素，就是模拟的大堆进行插入操作，只是这些值已经有了，相当于插好了，只是需要进行调整

如下是我们将数组在逻辑结构上画成堆的样子，但不是堆，不满足堆的性质，所以需要我们进行调整算法

看下面：从第二层开始进行调整，根据下标来进行的，依次类推，会一直调整到最后一个元素

 流程图：手绘的 红色箭头表示所在下标（位置） 黑色就是结束一次向上调整函数

堆也就建立如下图：是大堆，但是不是有序的，让他变成有序，等会将考虑，一口吃不成胖子

 向上调整的算法：

下标为0开始的

 2、向下调整算法实现大堆的建立：

在堆的删除就是使用的向下调整算法，我们会发现删除的前提是它是堆，那么若是将数组的首元素直接向下调整是不行的因为此时这个数组逻辑上看它就不是堆，若是左子树、右子树是大堆，那么我就可以直接向下调整；

我们想办法将左右子树变成大堆；是不是可以逆向思维呢？叶子节点是不可以向下调整的，那我找到叶子结点的父节点，是不是就可以进行调整，一点一点从数组的最后一个元素开始，但是看图我们会发现实际是从第一个非子叶结点开始的 将上图变左、右子树，最后到了根结点，让根结点向下调整，就完成了大堆的建立

如下图流程：

向下调整的算法： 

从叶子结点的父亲开始传，这个不就是通过孩子节点求父亲的公式么；开始传

 3、排序：

简单多了类似堆的删除（假删除并不是真的删除o）；是将根结点先与最后一个结点互换，然后将

元素个数n-1  将新的元素个数传上去进行向下调整

 因为堆顶元素在这个堆中用远是最大的，所以不断的将堆顶元素和堆的最后一个元素进行交换，直到将这个大堆变成只剩下根结点的堆，此时数据变成有序了

这个过程我的堆的元素个数在不断减小

 代码实现升序：

typedef int HpDataType;
//交换数据
void Swp(HpDataType* p1, HpDataType* p2)
{
	assert(p1 && p2);
	HpDataType tmp = *p2;
	*p2 = *p1;
	*p1 = tmp;
}

//大堆：向上调整,child 为孩子
void AdjustUpBig(HpDataType* a, int child)
{
	assert(a);
	//parent 父亲结点
	int  parent = (child - 1) / 2;
	//循环的进行从3个方面考虑：
	// 1、初始条件
	// 2、中间过程
	// 3、结束条件
	//循环有2种写法：
	while (child > 0 && a[child] > a[parent])
	{
		//互换；
		Swp(&a[child], &a[parent]);
		child = parent;
		parent = (child - 1) / 2;
	}
	
}
//大堆:向下调整  //数组  元素个数  parent 父亲节点
void AdjustDownBig(HpDataType* a, int n, int parent)
{
	assert(a);
	//用到假设法：我们要保证我的父亲节点比最大的儿子节点大或者相等；假设左孩子大
	int child = 2 * parent + 1;
	while (child < n)
	{//判断一下,完全二叉树，有可能会有有孩子不存在的情况
		if (a[child] < a[child + 1] && child + 1 < n)
		{
			//拿孩子大的去和父亲比较
			child = child + 1;
		}
		if (a[child] > a[parent])
		{
			Swp(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}

	}

}

//打印
void Prin(int* a, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
}

//大堆：变量含义：数组  元素个数
//大堆：向上调整实现升序
void HpBig(int* a, int n)
{
	int i;
	//从第二层的第一孩子开始向上调整建堆
	for (i = 1; i < n; i++)
	{
		AdjustUpBig(a, i);
	}
	int k = n;
	//排序
	for (i = n - 1; i > 0; i--)
	{
		Swp(&a[0], &a[i]);
		k--;
		AdjustDownBig(a, k, 0);
	}
	//打印
	Prin(a, n);
}
//大堆：向下调整实现升序
void HpBig2(int* a, int n)
{
	int i;	
	//向下调整建堆
	for(i = (n - 1-1); i >=0; i--)
	{
		AdjustDownBig(a, n, i);
	}
	int k = n;
	//排序
	for (i = n - 1; i > 0; i--)
	{
		Swp(&a[0], &a[i]);
		k--;
		AdjustDownBig(a, k, 0);
	}
	//打印
	Prin(a, n); 

}

三、降序的实现：通过建小堆实现

>思路：

1. 将待排序数组构造成一个小堆
2. 这个序列最小值在堆顶
3. 将其与末尾元素进行交换，末尾变成最小值
4. 将剩下的n-1个结点重新调整为小堆
5. 再次将最小值与此时（为n-1个结点的小堆）的末尾元素交换
6. 重复下去，到最后就是有序的了，整个数组最大的元素此时在栈顶

1、向上调整算法实现小堆的建立：了解即可

思路一样的，流程图都是大差不差的，无非就是变成了孩子小于爹就交换

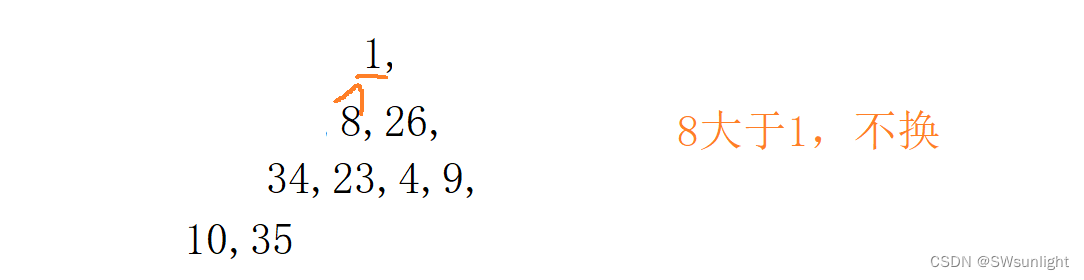
2、向下调整算法实现小堆的建立：

3、排序：

都是大堆实现过的，思路就是一样的，就是要注意性质，决定了符号（大于还是小于）

代码：

//因为是直接复制过来的，所以用来Typedef改名
typedef int HpDataType;
//交换数据
void Swp(HpDataType* p1, HpDataType* p2)
{
	assert(p1 && p2);
	HpDataType tmp = *p2;
	*p2 = *p1;
	*p1 = tmp;
}
//打印
void Prin(int* a, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
}
//小堆：向上调整完成降序
void HpSmall(int* a, int n)
{
	int i;
	//从第二层开始调整
	for (i = 1; i < n; i++)
	{
		AdjustUpSmall(a, i);
	}
	int k = n;
	//排序：
	for (i = (n - 1-1); i > 0; i--)
	{
		Swp(&a[0], &a[i]);
		k--;
		AdjustDownSmall(a, k, 0);
	}
	//打印
	Prin(a, n);


}
//小堆：向下调整实现降序
void HpSmall2(int* a, int n)
{
	int i;
	
	//建堆
	for(i = n - 1; i >=0; i--)
	{
		AdjustDownSmall(a, n, i);
	}
	int k = n;
	//排序：
	for (i = n - 1; i > 0; i--)
	{
		Swp(&a[0], &a[i]);
		k--;
		AdjustDownSmall(a, k, 0);
	}
	//打印
	Prin(a, n);
}

四、建堆的时间复杂度计算：

向下调整算法的时间复杂度

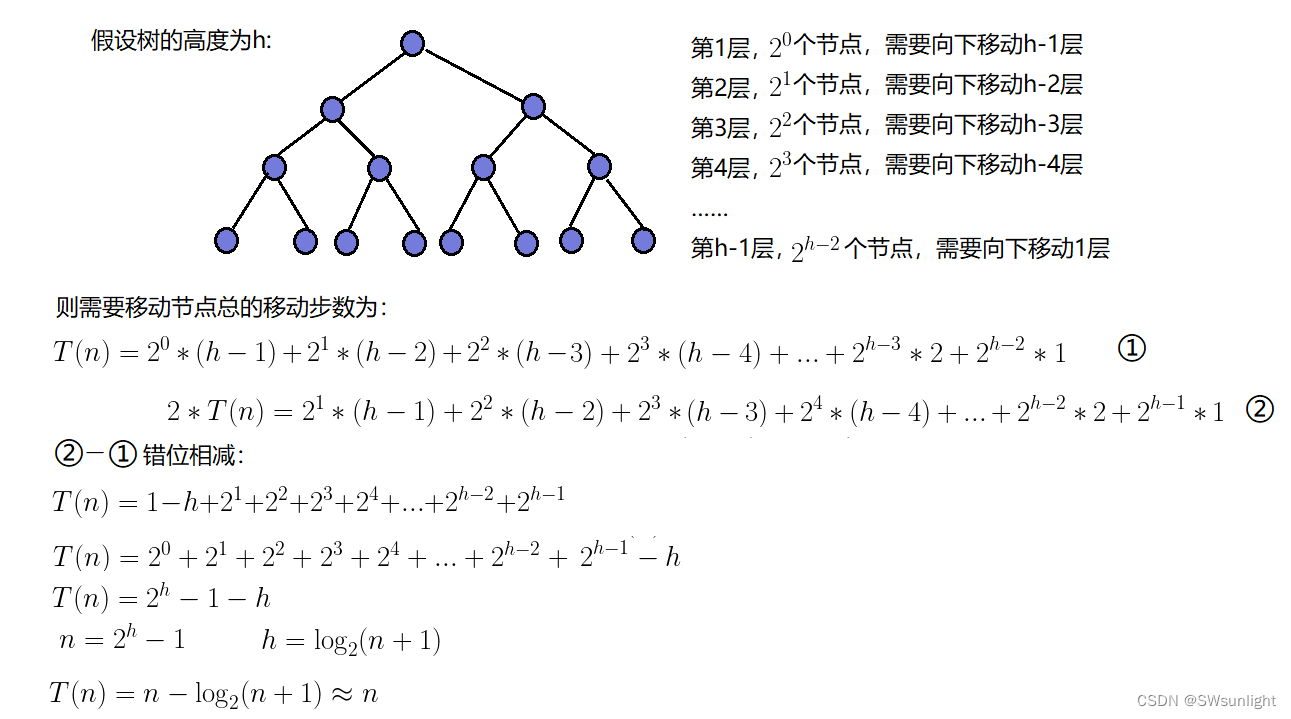
时间复杂度为O(N)

---

向上调整算法的时间复杂度：

计算过程和上面雷同

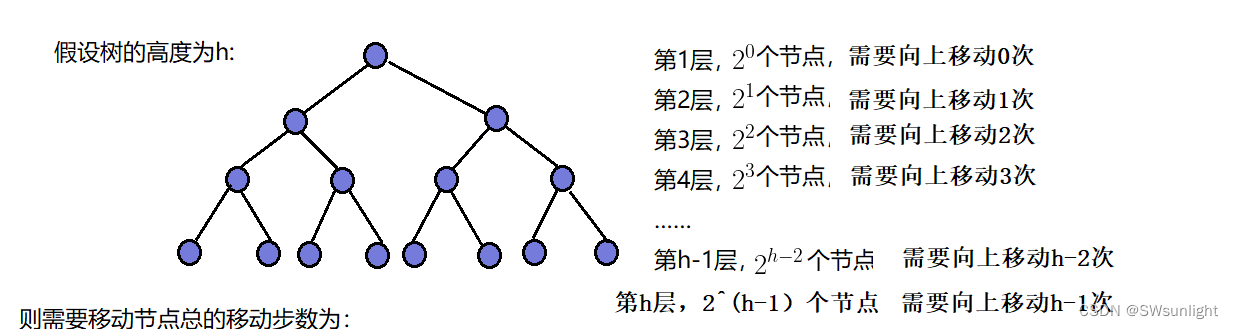
时间复杂度：O（N*logN）

我们发现这2个不同的特点是：

向下调整：结点数量越多，调整次数越少；（反比）

向上调整：结点数量越多，调整次数越多；（正比）

---

五、总结：

        对于堆排序的实现，其实只要彻底掌握了堆的实现即可完成，对于向上向下调整算法有了理解，其实堆排序的实现也就不难了，原理都是一样的，非常类似，有了大堆实现升序的思路，降序也就一起出来了，画图更有助于理解。本文图不是很好看，还在努力提升画图技术！！注意的是向上和向下调整建堆的时间复杂度是不一样的，向下调整对于堆排序是最好的选择

  完                  结                           撒                花