数据结构（3）线段树基础

news2024/12/28 2:23:51

活动 - AcWing

参考《算法竞赛进阶指南》-lyd

一、概述

1.简述、所需空间

线段树是一种基于分治思想的二叉树结构，用于区间上的信息统计。与树状数组相比，线段树是一种更通用的数据结构。

线段树每个节点代表一个区间。线段树具有唯一根节点，代表整个统计区间。

叶节点代表一个长度为1的元区间。

对于每个内部节点，它的左子节点是[l,mid],右子节点是[mid+1,r]，其中mid=（l+r）/2向下取整。

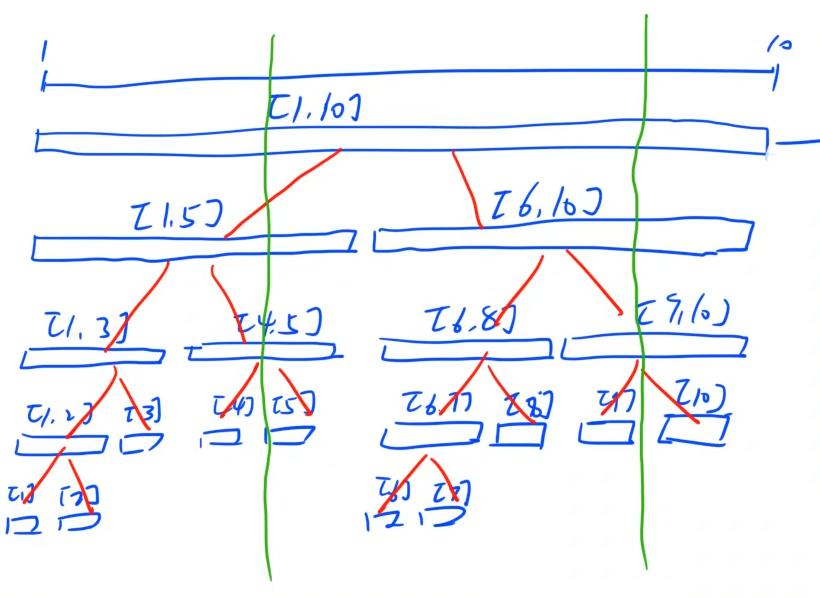
上图展示了一棵线段树，可以发现除去树的最后一层，整棵线段树一定是一棵完全二叉树。

深度为logn。因此我们可以按照静态链表的“父子2倍”的结点编号方法。

这样就可以用一个结构体存储线段树结点。

理想情况下：N个结点的满二叉树有N+N/2+N/4+....+2+1=2N-1。但是要空出最后一层的空余，因此保存线段树的数组长度不能小于4*N。才能保证数组不会越界。

2.相关操作

线段树基本用途是对序列进行维护。线段树的二叉树结构可以很方便的从下到上传递信息。以区间最大值为例

（1）线段树的建树

首先定义节点结构体

struct Node{
    int l,r;
    int d;
}tr[4*N];

建树操作：即根据原始序列建树，使得tr数组内节点l，r能够被初始化，d根据原始序列被初始化。

思想：信息从上到下传递，因此采用递归思想。传入当前节点的编号，设定l，r。然后折半递归左右子树，最后根据左右子树信息修改当前节点信息。递归边界条件是递归到叶子节点。

void pushup(Node &u,Node &l,Node &r)
{
    u.d=max(l.d,r.d);
}

void pushup(int u)
{
    pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}


void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[r]};
    else
    {
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid);
        build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

（2）单点修改

和树状数组类似，单点修改之后一步步递归回去。

首先递归边界是递归到目标叶子节点，修改之后return

如果不是叶子节点，则判断目标节点在左半边还是右半边，递归目标区间。

递归之后根据子节点信息修改当前节点信息。

void modify(int u,int x,int v)
{
    if(tr[u].l==tr[u].r) tr[u].d=v;
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}

 (3)区间查询

过程和复杂度分析：
对于一个Node节点,范围是[p1,p2]，可能有以下情况：

  1. l<=p1<=p2<=r，即查询区间完全覆盖当前节点，则直接返回上该节点信息
  2. 如果只有l在节点之内： 
    1. l>mid，则说明只会继续递归右子树
    2. l<=mid，则只会递归左子树。                
  3. 如果只有r在节点之内，则与2情况类似
  4. 如果l和r都在节点之内，
    1. 如果l，r都在mid左侧或右侧，则只会递归一棵子树
    2. 如果分别在两侧，则递归左右子树。

那么只有4(2)情况会分别递归左右两颗子树，而这种情况最多发生一次，因为这之后在节点上就会变成2或3情况。因此查询复杂度为O（2logn）。

二、例题

1.最大数

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 200010;

int m, p;
struct Node
{
    int l, r;
    int v;  // 区间[l, r]中的最大值
}tr[N * 4];

void pushup(int u)  // 由子节点的信息，来计算父节点的信息
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}



void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}


int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;   // 树中节点，已经被完全包含在[l, r]中了

    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (l <= mid) v = query(u << 1, l, r);
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));

    return v;
}

void modify(int u,int x,int v)
{
    if(tr[u].l==tr[u].r) tr[u].v=v;

    else 
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }

}
int main()
{
    cin>>m>>p;
    int last=0;
    build(1,1,m);
    int n=0;
    while(m--)
    {
        char op[2];
        int x;
        cin>>op>>x;
        if(*op=='Q')
        {
            last=query(1,n-x+1,n);
            cout<<last<<endl;
        }
        else
        {
            modify(1,n+1,((LL)last+x)%p);
            n++;
        }
    }
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5199364/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2.你能回答这些问题吗

 查询最大连续子段和。是区间信息，所以考虑线段树。

那么我们就要考虑如何状态转移，即如何用子节点的值更新父节点。

在线段树的每个节点上，除了区间端点外，我们需要再维护4个信息：区间sum，区间最大连续子段和tmax，紧靠左端的最大连续子段和lmax，紧靠右端的最大连续子段和rmax。

线段树的整体框架不变，只需要完善build和modify函数中从下往上传递的信息。

void pushup(Node &u,Node &l,Node &r)
{
    u.sum=l.sum+r.sum;
    u.lmax=max(l.lmax,l.sum+r.lmax);
    u.rmax=max(r.rmax,r.sum+l.rmax);
    u.tmax=max(max(l.tmax,r.tmax),l.rmax+r.lmax);
}

void pushup(int u)
{
    pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}

完整代码：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N =500010;

struct Node{
    int l,r;
    int sum,lmax,rmax,tmax;
}tr[4*N];

int n,m;
int w[N];

void pushup(Node &u,Node &l,Node &r)
{
    u.sum=l.sum+r.sum;
    u.lmax=max(l.lmax,l.sum+r.lmax);
    u.rmax=max(r.rmax,r.sum+l.rmax);
    u.tmax=max(max(l.tmax,r.tmax),l.rmax+r.lmax);
}

void pushup(int u)
{
    pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}

void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[r],w[r],w[r],w[r]};
    else
    {
        tr[u]={l,r};//注意要更新l，r
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int x,int v)
{
    if(tr[u].l==tr[u].r) tr[u]={x,x,v,v,v,v};
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}
Node query(int u,int l,int r)
{
    //if(tr[u].l==tr[u].r) return tr[u];  第一次写错的地方
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u];
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(l>mid) return query(u<<1|1,l,r);
        else if(r<=mid) return query(u<<1,l,r);
        else
        {
            auto left=query(u<<1,l,r);
            auto right=query(u<<1|1,l,r);
            Node res;
            pushup(res,left,right);
            return res;
        }
    }
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    build(1,1,n);
    int k,x,y;
    while(m--)
    {
        cin>>k>>x>>y;
        if(k==1)
        {
            if(x>y) swap(x,y);
            cout<<query(1,x,y).tmax<<endl;
        }
        else
            modify(1,x,y);
    }
    return 0;

}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5199473/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3.区间最大公约数

 区间修改和区间查询。

首先思考一下能不能把区间修改转变为单点修改。根据“更相减损术”：gcd(x,y)=gcd(x,y-x)

可以证明对多个整数仍然成立：

 

 d能整除a1 a2-a1  则d能整除a1+（a2-a1）

所以

 因此（差分序列的最大公约数和原数组区间左端）最大公约数 等于原数组的区间最大公约数（具体如上图）。

所以我们构建差分序列b。b[1]可为任意值，用线段树维护序列b的区间最大公约数。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N =500010;
typedef long long LL;

int n,m;
struct Node{
    int l,r;
    LL sum,d;
}tr[4*N];
LL w[N];

LL gcd(LL a,LL b)
{
    return b?gcd(b,a%b):a;
}

void pushup(Node &u,Node &l,Node &r)
{
    u.sum=l.sum+r.sum;
    u.d=gcd(l.d,r.d);
}
void pushup(int u)
{
    pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}


void build(int u,int l,int r)
{
    if(l==r)
    {
        LL b=w[l]-w[l-1];
        tr[u]={l,r,b,b};
    }
    else
    {
        tr[u].l=l,tr[u].r=r;
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int x,LL v)
{
    if(tr[u].l==tr[u].r) 
    {
        LL b=tr[u].sum+v;
        tr[u]={x,x,b,b};
    }
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }

}

Node query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u];
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(r<=mid) return query(u<<1,l,r);
        else if(l>mid) return query(u<<1|1,l,r);
        else
        {
            auto left=query(u<<1,l,r);
            auto right=query(u<<1|1,l,r);
            Node res;
            pushup(res,left,right);
            return res;
        }
    }
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);

    int l,r;
    LL d;
    char op[2];

    while(m--)
    {
        cin>>op>>l>>r;
        if(*op=='Q')
        {
            auto left=query(1,1,l);
            Node right={0,0,0,0};
            if(l+1<=r) right=query(1,l+1,r);
            cout<<abs(gcd(left.sum,right.d))<<endl;
        }
        else
        {
            cin>>d;
            modify(1,l,d);
            if(r+1<=n) modify(1,r+1,-d);
        }
    }
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5199926/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/168492.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

关于KDDockWidget源码修改和自定义

关于KDDockWidget源码修改和自定义

前言 前面的文章介绍过KDDockWidget的基本使用及示例&#xff0c;文章在这里&#xff1a; KDDockWidgets源码编译及安装 qml dockwidget窗口停靠 QML KDDockWidget 实现 tabwidget效果&#xff08; 窗口可独立浮动和缩放&#xff09; 今天主要记录一些在KDDockWidget源码中的…
阅读更多...
来自元宇宙的声音：Chord Hero

来自元宇宙的声音：Chord Hero

这一集&#xff0c;我们邀请了 Chord Hero 的联合创始人兼行政总裁 Anthony Chau 来谈谈促使他加入 The Sandbox 元宇宙的原因以及即将在即将到来的游戏赛季推出的第一个项目。 请告诉我们更多关于 Chord Hero 的信息吧。 Chord Hero 通过一系列实体和数字产品让学习音乐变得有…
阅读更多...
视图（view）

视图（view）

1、视图&#xff1a;&#xff08;了解内容&#xff09; 就是站在不同的角度去看待同一份数据。 视图是MySQL服务器中的一个对象&#xff0c;用于存储查询语句&#xff0c;目的的提高查询语句的使用效率&#xff0c;避免在多处地方重复性开发相同的查询语句。 - 将查询语句交给一…
阅读更多...
Transformer学习笔记1

Transformer学习笔记1

模型分类&#xff1a;GPT类型&#xff1a; auto-regressive&#xff08;decoder模型&#xff0c;过去时刻的输出也是现在的输入&#xff0c;例如要得到y8还需要知道y1到y7&#xff0c;但不能使用y9&#xff0c;例如用于文本生成任务&#xff09;GPTGPT2CTRLTransformer XLBERT类…
阅读更多...
Docker 容器监控

Docker 容器监控

目录 cAdvisor 安装cAdvisor 使用Prometheus监控cAdvisor cAdvisor暴露的Prometheus指标 容器指标 1. 文档&#xff1a; 2. 指标 硬件指标 1. 文档&#xff1a; 2. 指标&#xff1a; Node Exporter 安装Node Exporter 1. 启动容器&#xff0c;默认端口为9100 2. …
阅读更多...
2023免费电脑c盘磁盘数据恢复软件EasyRecovery

2023免费电脑c盘磁盘数据恢复软件EasyRecovery

无论是台式机还是笔记本电脑&#xff0c;我们都习惯将其划分成多个大小不一的磁盘&#xff0c;有的是用于安装系统&#xff0c;有的则是用于存储文件。今天小编就和大家解答一下关于电脑磁盘的问题&#xff0c;电脑只剩c盘是硬盘坏了吗&#xff0c;电脑突然就剩c盘怎么恢复。想…
阅读更多...
【BP靶场portswigger-客户端16】测试WebSockets安全漏洞-3个实验（全）

【BP靶场portswigger-客户端16】测试WebSockets安全漏洞-3个实验（全）

前言&#xff1a; 介绍&#xff1a; 博主&#xff1a;网络安全领域狂热爱好者&#xff08;承诺在CSDN永久无偿分享文章&#xff09;。 殊荣&#xff1a;CSDN网络安全领域优质创作者&#xff0c;2022年双十一业务安全保卫战-某厂第一名&#xff0c;某厂特邀数字业务安全研究员&…
阅读更多...
CMMI落地4大工具 助力CMMI3-5级高效落地

CMMI落地4大工具 助力CMMI3-5级高效落地

CMMI落地4大工具近日正式上线&#xff0c;全面支持CMMI3-5级&#xff0c;助力CMMI高效落地。CoCode旗下的Co-ProjectV3.0智能项目管理平台全新发布&#xff1a;CMMI成熟度自测工具、量化管理工具&#xff08;组织级过程改进工具和量化项目管理工具&#xff09;、组织级过程资产…
阅读更多...
分享视频剪辑必备的三个素材软件（配音/文案/图片）

分享视频剪辑必备的三个素材软件（配音/文案/图片）

hello&#xff0c;大家好&#xff0c;相信现在很多小伙伴都需要制作视频&#xff0c;无论是从事短视频行业&#xff0c;还是单纯想分享生活视频的都需要对视频进行简单的处理吧&#xff1f;有时候会需要介绍视频内容或是给视频增加点配音&#xff0c;来让视频不那么单调&#x…
阅读更多...
C++11 解决内存泄露问题的智能指针：shared_ptr、unique_ptr、weak_ptr

C++11 解决内存泄露问题的智能指针：shared_ptr、unique_ptr、weak_ptr

我们经常听到内存泄漏&#xff0c;但是对这个抽象的概念一直没有什么理解&#xff0c;比如产生内存泄漏又将如何&#xff0c;我平时写程序从来不考虑这个等等。这篇的目的&#xff1a;第一&#xff0c;给大家实验实验内存泄露带来的问题&#xff0c;让大家直观感受内存泄露。第…
阅读更多...
[数据结构基础]链式二叉树及其前序、中序和后序遍历

[数据结构基础]链式二叉树及其前序、中序和后序遍历

一. 链式二叉树的结构和实现 1.1 链式二叉树的结构 链式二叉树&#xff0c;即使用链来表示一颗二叉树。链式二叉树的存储又可分为二叉链和三叉链&#xff0c;其中二叉链存储节点数据、指向左子节点的指针和指向右子节点的指针&#xff0c;三叉链相对于二叉链多存储指向父亲节…
阅读更多...
一种基于肌电信号运动起点、波峰、终点实时自动检测的方法

一种基于肌电信号运动起点、波峰、终点实时自动检测的方法

一种基于肌电信号运动起点、波峰、终点实时自动检测的方法 (⊙o⊙)…，这篇是我写收费文章的第一篇。咱也尝试下知识付费，哈哈。 先看下效果，在给定理想正弦波的情况下，可以准确识别到正弦波的起点、波峰和终点。机器实拍图如下。 因为我的实际环境没有专利里面那么复杂，所…
阅读更多...
Android 蓝牙开发——基础开发（三）

Android 蓝牙开发——基础开发（三）

蓝牙开发这部分主要以 APP 端调用功能接口为开始&#xff0c;到 Framework 端的调用流程&#xff0c;最后到调用状态机结束&#xff0c;不涉及蓝牙协议栈的开发分析。 一、BluetoothAdapter 1、APP获取适配器 蓝牙权限 <mainifest><uses-permission android:name&…
阅读更多...
3.ESP32-S2/S3 USB 挂载SPI-SD，当作U盘使用，无线U盘

3.ESP32-S2/S3 USB 挂载SPI-SD，当作U盘使用，无线U盘

使用的 IDF_4.4 C语言开发 1.ESP32-S2/S3 USB烧录 输出日志 2.ESP32-S2/S3 USB 挂载内部Flash&#xff0c;当作U盘使用&#xff0c;无线U盘 3.ESP32-S2/S3 USB 挂载SPI-SD&#xff0c;当作U盘使用&#xff0c;无线U盘 目录1.打开 usb_msc_wireless_disk 工程 Confinguration2.…
阅读更多...
数学建模-数学规划（Matlab）

数学建模-数学规划（Matlab）

目录 一、线性规划求解 二、非线性规划问题 三、整数规划&#xff08;包括0-1规划&#xff09; 四、最大最小化模型 五、多目标规划模型 注意&#xff1a;代码文件仅供参考&#xff0c;一定不要直接用于自己的数模论文中国赛对于论文的查重要求非常严格&#xff0c;代码雷同…
阅读更多...
微服务Spring Boot 整合 Redis 实现 UV 数据统计

微服务Spring Boot 整合 Redis 实现 UV 数据统计

文章目录⛄引言一、HyperLoglog基础用法⛅HyperLoglog 基本语法、命令⚡HyperLoglog 命令完成功能实现二、UV统计 测试百万数据的统计☁️什么是UV统计⚡使用SpringBoot单元测试进行测试百万数据统计⛵小结⛄引言 本文参考黑马 点评项目 在各个项目中&#xff0c;我们都可能需…
阅读更多...
DaVinci：限定器 - HSL

DaVinci：限定器 - HSL

调色页面&#xff1a;限定器Color&#xff1a;Qualifier限定器 - HSL Qualifier - HSL根据色相、饱和度和亮度等来选择画面上的对应区域&#xff0c;从而将二级调色与修饰限制在一定的范围。选择范围Selection Range拾取器Picker在检视器画面上按住并拖动&#xff0c;可以选择相…
阅读更多...
Linux FHS结构

Linux FHS结构

FHS是Filesystem Hierarchy Standard&#xff08;文件系统层次化标准&#xff09;的缩写&#xff0c;多数Linux版本采用这种文件组织形式&#xff0c;类似于Windows操作系统中c盘的文件目录&#xff0c;FHS采用树形结构组织文件。FHS定义了系统中每个区域的用途、所需要的最小构…
阅读更多...
格式化输出

格式化输出

1、golang不同输出语句的区别&#xff1a; 特点PrintPrintlnPrintf输出内容到控制台&#xff08;终端输出&#xff09;SprintSprintlnSprintf输出内容为字符串FprintFprintlnFprintf输出内容到文件特点 输出内容不会换行。 不能格式化字符串。 输出内容换行,。 不能格式化字符…
阅读更多...
【C语言进阶】枚举与联合体

【C语言进阶】枚举与联合体

目录一&#xff1a;枚举1.1&#xff1a;枚举类型的定义&#xff1a;1.1&#xff1a;枚举的优点&#xff1a;1.2&#xff1a;枚举的使用&#xff1a;二&#xff1a;联合&#xff08;共用体&#xff09;2.1&#xff1a;联合类型的定义&#xff1a;2.2&#xff1a;联合类型的特点&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023