文章目录
- 大跟堆介绍
- 大跟堆的结构
- 大跟堆的应用场景
- 大跟堆的代码实现
大跟堆介绍
大根堆(Max Heap)是一种特殊的二叉树结构,它满足以下两个条件:
1.完全二叉树:大根堆是一棵完全二叉树,即除了最后一层外,其余每一层的节点都是满的,最后一层的节点都集中在最左边。
2.堆性质:每个节点的值都大于或等于其子节点的值。
大根堆的典型操作包括插入,获取root节点的最大值。
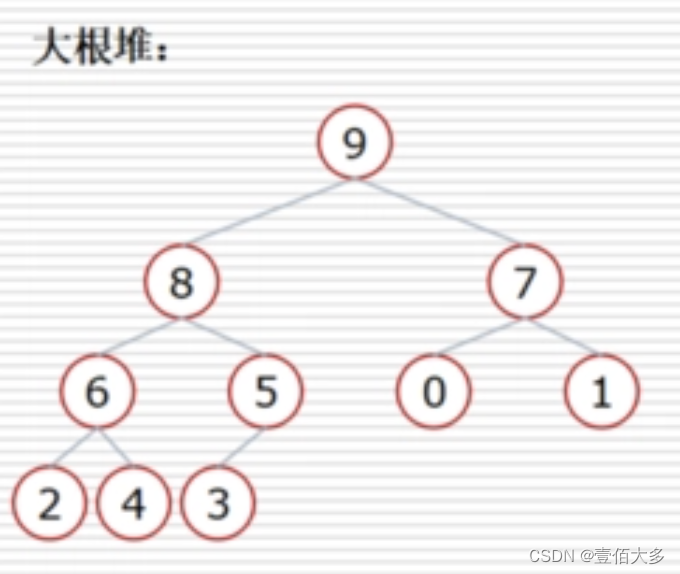
大跟堆的结构
大根堆的结构
大根堆可以用数组来表示,因为它是一棵完全二叉树。对于一个存储在数组中的大根堆:
根节点的索引为 0。
给定一个节点的索引位置i:
父节点的索引为 (i - 1) / 2。
左子节点的索引为 2 * i + 1。
右子节点的索引为 2 * i + 2。
大跟堆的应用场景
大根堆(Max Heap)在许多算法和应用中都有重要的作用,特别是在需要频繁访问最大元素的场景中。以下是一些常见的应用场景:
- 优先队列
优先队列是一种特殊的队列,每次出队的元素都是队列中优先级最高的元素。大根堆可以用来实现优先队列,其中堆顶元素始终是优先级最高的元素。
应用举例:
操作系统的任务调度:调度器选择优先级最高的任务进行执行。
网络数据包处理:路由器处理优先级最高的数据包。 - 堆排序
堆排序是一种利用堆数据结构设计的排序算法。其基本思想是将待排序序列构建成一个大根堆,此时整个序列的最大值即为堆顶元素。将堆顶元素移出堆(与堆的最后一个元素交换),然后对剩余元素重新构建堆,反复执行上述操作,直到所有元素有序。
应用举例:
大数据集的排序:在需要对大量数据进行排序时,堆排序的空间效率较高。 - 动态数据流中的最大值
在处理动态数据流时,使用大根堆可以实时维护当前数据流中的最大值。
应用举例:
股票交易系统:实时维护当前交易中的最大交易量。
传感器数据监控:实时监控传感器数据流中的最大值。 - 找到第 K 大的元素
在一个无序数组中查找第 K 大的元素,可以使用大根堆来实现。首先构建一个包含数组中前 K 个元素的大根堆,然后遍历数组剩余元素,如果当前元素小于堆顶元素,则替换堆顶元素并调整堆,最终堆顶元素即为第 K 大的元素。
应用举例:
排名系统:在一组分数中找到第 K 高的分数。
数据分析:在一组数据中找到第 K 大的数据点。 - 合并多个有序序列
在合并多个有序序列时,可以使用大根堆来保持当前最小元素的顺序。将每个序列的首元素插入大根堆,然后每次取出堆顶元素并插入其所在序列的下一个元素,直到所有元素都被处理完毕。
应用举例:
外部排序:当数据量大到无法全部放入内存时,可以先将数据分块排序,然后合并多个有序块。
多路归并排序:将多个有序的输入流合并为一个有序的输出流。 - 图的最短路径算法(如 Dijkstra 算法)
在 Dijkstra 算法中,需要使用优先队列来选择当前未访问节点中距离起点最近的节点。大根堆可以用来实现这个优先队列,以保证每次都能高效地选择最短路径的下一步节点。
应用举例:
地图导航系统:计算从一个地点到另一个地点的最短路径。
网络路由优化:寻找数据包在网络中传输的最优路径。 - 事件驱动模拟
在事件驱动的模拟系统中,需要按照事件的发生时间顺序来处理事件。使用大根堆可以有效地管理和调度这些事件。
应用举例:
离散事件模拟:如模拟交通流、制造过程等。
计算机图形学:处理动画中事件的时间调度。
大跟堆的代码实现
插入操作:
插入新元素时,将元素添加到数组的末尾(完全二叉树的最后一个位置),然后进行“上浮”操作(也称为堆化)以恢复堆的性质。
上浮操作:
将新元素与其父节点比较,如果大于父节点,则交换位置,继续向上比较,直到元素小于或等于父节点,或者到达根节点。
public void insert(int key) {
if (size == capacity) {
throw new RuntimeException("Heap is full");
}
heap[size] = key; // 将新元素放在堆尾
int current = size;
size++;
// 上浮操作
while (current != 0 && heap[parent(current)] < heap[current]) {
swap(parent(current), current);
current = parent(current);
}
}
2.删除最大值操作:
删除最大值(根节点)时,将数组的最后一个元素移动到根节点位置,然后进行“下沉”操作(也称为堆化)以恢复堆的性质。
下沉操作:
将根节点与其左右子节点比较,如果小于其中一个子节点,则与较大的子节点交换位置,继续向下比较,直到元素大于或等于子节点,或者到达叶节点。
public int extractMax() {
if (size <= 0) {
throw new RuntimeException("Heap is empty");
}
int root = heap[0]; // 保存根节点
heap[0] = heap[size - 1]; // 将最后一个元素移到根节点位置
size--;
// 下沉操作
maxHeapify(0);
return root;
}
private void maxHeapify(int i) {
int largest = i;
int left = leftChild(i);
int right = rightChild(i);
if (left < size && heap[left] > heap[largest]) {
largest = left;
}
if (right < size && heap[right] > heap[largest]) {
largest = right;
}
if (largest != i) {
swap(i, largest);
maxHeapify(largest);
}
}
3.交换元素:
在堆的操作过程中,经常需要交换两个节点的位置。
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
4.完整的大根堆实现
以下是大根堆的完整实现,包括构造函数、插入操作、删除最大值操作和辅助方法。
public class MaxHeap {
private int[] heap;
private int size;
private int capacity;
// 构造函数
public MaxHeap(int capacity) {
this.capacity = capacity;
this.heap = new int[capacity];
this.size = 0;
}
// 获取父节点索引
private int parent(int i) { return (i - 1) / 2; }
// 获取左子节点索引
private int leftChild(int i) { return 2 * i + 1; }
// 获取右子节点索引
private int rightChild(int i) { return 2 * i + 2; }
// 插入新元素
public void insert(int key) {
if (size == capacity) {
throw new RuntimeException("Heap is full");
}
heap[size] = key; // 将新元素放在堆尾
int current = size;
size++;
// 上浮操作
while (current != 0 && heap[parent(current)] < heap[current]) {
swap(parent(current), current);
current = parent(current);
}
}
// 提取最大元素(根节点)
public int extractMax() {
if (size <= 0) {
throw new RuntimeException("Heap is empty");
}
int root = heap[0]; // 保存根节点
heap[0] = heap[size - 1]; // 将最后一个元素移到根节点位置
size--;
// 下沉操作
maxHeapify(0);
return root;
}
// 下沉操作
private void maxHeapify(int i) {
int largest = i;
int left = leftChild(i);
int right = rightChild(i);
if (left < size && heap[left] > heap[largest]) {
largest = left;
}
if (right < size && heap[right] > heap[largest]) {
largest = right;
}
if (largest != i) {
swap(i, largest);
maxHeapify(largest);
}
}
// 交换元素
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
// 主函数示例
public static void main(String[] args) {
MaxHeap maxHeap = new MaxHeap(10);
maxHeap.insert(3);
maxHeap.insert(1);
maxHeap.insert(4);
maxHeap.insert(1);
maxHeap.insert(5);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(6);
maxHeap.insert(5);
System.out.println("Extracted max: " + maxHeap.extractMax());
System.out.println("Extracted max: " + maxHeap.extractMax());
System.out.println("Extracted max: " + maxHeap.extractMax());
}
}