目录
- 一、SVM (Support Vector Machine) 概述
- (一)支持向量机SVM的主要特点
- (二)支持向量与间隔最大化
- (三)线性可分/不可分
- (四)软间隔 (soft margin) 与核技巧 (kernel trick)
- (五)核技巧配合软间隔解决线性不可分问题
- 二、硬间隔解决线性可分问题
- (一)线性可分的决策超平面
- (二)硬间隔、决策边界和支持向量之间关系
- (三)最大化间隔宽度
- (四)最小化损失函数及其求解方法
- (五)带不等式约束的优化问题的解与KKT条件
- (六)拉格朗日对偶问题及其求解
- 三、软间隔解决线性不可分问题
- (一)软间隔SVM分类器的核心思想
- (二)软间隔SVM分类器的损失函数
- (三)核技巧使用映射函数升维解决分类问题
- (四)软间隔+核技巧的SVM优化问题
- (五)拉格朗日对偶问题与核函数
- (六)常见的核函数
- 四、scikit-learn中的SVM分类器及其主要参数
- (一)多分类的情形
- (二)SVM的属性和方法
- 五、支持向量机应用示例
一、SVM (Support Vector Machine) 概述
(一)支持向量机SVM的主要特点
- 支持向量机 SVM 是一种既可以用于分类、也可以用于回归问题的监督学习算法。
- SVM 的主要思想是找到一个具有最大间隔 (max margin) 的分类决策超平面,从而可以将不同类别的样本点分隔开。
- SVM 是一个非常强大的算法,因为它使用内积核函数将原始输入数据映射到高维空间,从而能够处理高维空间和非线性问题,并且能够有效地避免过拟合。
- SVM 的缺点是它对于大型数据集的计算成本很高,以及内积核函数的选择和调整需要一定的经验和技巧。
(二)支持向量与间隔最大化

图中深蓝色线便是决策边界,也称分离超平面;两条虚线之间宽度叫做间隔 (margin)。支持向量机的优化目标为——间隔最大化。
支持向量(红蓝加圈的点)确定决策边界位置;而其他数据并没有对决策起到任何作用。因此,SVM 对于数据特征数量远高于数据样本量的情况也有效(可以处理高维数据)。
(三)线性可分/不可分

- 线性可分问题采用硬间隔 (hard margin);即间隔内没有数据点。
- 支持向量机解决线性不可分问题,需要并用软间隔和核技巧。
(四)软间隔 (soft margin) 与核技巧 (kernel trick)

- 软间隔相当于一个缓冲区。使用软间隔分类时,允许有数据点侵入间隔,甚至超越间隔带。
- 核技巧将数据映射到高维特征空间,是一种数据升维。
(五)核技巧配合软间隔解决线性不可分问题

二、硬间隔解决线性可分问题
(一)线性可分的决策超平面
1、决策超平面定义
决策超平面定义为: f ( x ) = w T x + b = 0 f(x)=w^Tx+b=0 f(x)=wTx+b=0,其中 w w w 是超平面的法向量

接下来我们的目标是研究不同类别的支持向量间的间距如何用系数向量
w
w
w 和
b
b
b 表示出来。只要能表示出来这个间距,通过间距最大化就可能求出系数向量
w
w
w 和
b
b
b,这样就得到了决策面。
2、平面外一点到平面的距离

-
设 x x x 是平面上任一点, q q q 是平面外任一点,向量 a a a 是两者的连线,则有: a = q − x , w T + b = 0 a=q-x, w^T+b=0 a=q−x,wT+b=0
-
设向量 a a a 在法向量 w w w 方向的投影向量 d d d 的长度为 D D D,则 D = ∣ w T a ∣ ∣ ∣ w ∣ ∣ = ∣ w T ( q − x ) ∣ ∣ ∣ w ∣ ∣ = ∣ w T q + b ∣ ∣ ∣ w ∣ ∣ \begin{aligned}D=\frac{|w^Ta|}{||w||}=\frac{|w^T(q-x)|}{||w||}=\frac{|w^Tq+b|}{||w||}\end{aligned} D=∣∣w∣∣∣wTa∣=∣∣w∣∣∣wT(q−x)∣=∣∣w∣∣∣wTq+b∣
-
一般情况下距离不考虑正负。但是,对于分类问题,考虑距离正负便于判断点和超平面关系,因此去掉分子的绝对值符号,用 D > 0 D>0 D>0 表示 q q q 在平面上方;反之 D < 0 D<0 D<0 表示 q q q 在平面下方。
(二)硬间隔、决策边界和支持向量之间关系

-
硬间隔的下边界为 l 1 l_1 l1 , l 1 l_1 l1 到决策边界距离为 − h -h −h。而支持向量 C 在 l 1 l_1 l1 上,则有: w T x + b ∣ ∣ w ∣ ∣ = − h \begin{aligned}\frac{w^Tx+b}{||w||}=-h\end{aligned} ∣∣w∣∣wTx+b=−h
-
硬间隔的上边界为 l 2 l_2 l2, l 2 l_2 l2 到决策边界距离为 + h +h +h。而支持向量 A、B 在 l 2 l_2 l2 上,则有: w T x + b ∣ ∣ w ∣ ∣ = + h \begin{aligned}\frac{w^Tx+b}{||w||}=+h\end{aligned} ∣∣w∣∣wTx+b=+h
-
距离决策边界大于等于 + h +h +h 的样本点,标记为 y = + 1 y=+1 y=+1;距离决策边界小于等于 − h -h −h 的样本点,标记为 y = − 1 y=-1 y=−1,则有:
{ w T x + b ∣ ∣ w ∣ ∣ ≥ + h , y = + 1 w T x + b ∣ ∣ w ∣ ∣ ≤ − h , y = − 1 ⇒ ( w T x + b ) y ∣ ∣ w ∣ ∣ h ≥ 1 \left\{ \begin{array}{l} \begin{aligned}\frac{w^Tx+b}{||w||}≥+h,y=+1\end{aligned}\\[3ex] \begin{aligned}\frac{w^Tx+b}{||w||}≤-h,y=-1\end{aligned} \end{array} \right. \Rightarrow \frac{(w^Tx+b)y}{||w||h}≥1 ⎩ ⎨ ⎧∣∣w∣∣wTx+b≥+h,y=+1∣∣w∣∣wTx+b≤−h,y=−1⇒∣∣w∣∣h(wTx+b)y≥1
(三)最大化间隔宽度
为简化计算,令分母
∣
∣
w
∣
∣
h
=
1
||w||h=1
∣∣w∣∣h=1,则间隔上下边界的解析式变为:
{
w
T
x
+
b
=
+
1
w
T
x
+
b
=
−
1
\left\{ \begin{array}{l} w^Tx+b=+1 \\[1ex] w^Tx+b=-1 \end{array} \right.
{wTx+b=+1wTx+b=−1
则间隔宽度
2
h
=
2
∣
∣
w
∣
∣
2h=\frac{2}{||w||}
2h=∣∣w∣∣2,最大化间隔宽度可表示为
arg max
w
,
b
2
∣
∣
w
∣
∣
s
u
b
j
e
c
t
t
o
(
x
(
i
)
w
+
b
)
y
(
i
)
≥
1
,
i
=
1
,
2
,
3
,
.
.
.
,
n
\begin{aligned} &\argmax_{w,b} \frac{2}{||w||}\\[3ex] &subject \ to \ (x^{(i)}w+b)y^{(i)}≥1,i=1,2,3,...,n \end{aligned}
w,bargmax∣∣w∣∣2subject to (x(i)w+b)y(i)≥1,i=1,2,3,...,n
(四)最小化损失函数及其求解方法
最大化间隔宽度等价于求解下列带不等式约束的最小化问题:
arg min
w
,
b
∣
∣
w
∣
∣
2
2
=
w
T
w
2
=
w
⋅
w
2
s
u
b
j
e
c
t
t
o
(
x
(
i
)
w
+
b
)
y
(
i
)
≥
1
,
i
=
1
,
2
,
3
,
.
.
.
,
n
(a)式
\begin{aligned} &\argmin_{w,b} \frac{||w||^2}{2}=\frac{w^Tw}{2}=\frac{w\cdot w}{2}\tag*{(a)式}\\[3ex] &subject \ to \ (x^{(i)}w+b)y^{(i)}≥1,i=1,2,3,...,n \end{aligned}
w,bargmin2∣∣w∣∣2=2wTw=2w⋅wsubject to (x(i)w+b)y(i)≥1,i=1,2,3,...,n(a)式
-
求解方法1:因为 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2 是严格的凸函数,所以该问题属于经典的凸优化问题,可以用 QP (二次规划) 算法求解。
-
求解方法2:通过拉格朗日乘子法,把上述带约束的最小化问题转化成无约束的最小化问题:
L ( w , b , λ ) = w ⋅ w 2 + ∑ i = 1 n λ i ( 1 − y ( i ) ( x ( i ) w + b ) ) (b)式 L(w,b,\lambda)=\frac{w\cdot w}{2}+\sum_{i=1}^n\lambda_i(1-y^{(i)}(x^{(i)}w+b))\tag*{(b)式} L(w,b,λ)=2w⋅w+i=1∑nλi(1−y(i)(x(i)w+b))(b)式 其中, λ = [ λ 1 λ 2 ⋯ λ n ] T \lambda=\left[\begin{matrix}\lambda_1 \ \lambda_2 \ \cdots \ \lambda_n\end{matrix} \right]^T λ=[λ1 λ2 ⋯ λn]T
(五)带不等式约束的优化问题的解与KKT条件
根据优化理论,上述(a)式子存在最优解的充要条件是满足如下KKT条件:
K
T
T
条件
{
∂
L
(
w
,
b
,
λ
)
∂
w
=
0
,
∂
L
(
w
,
b
,
λ
)
∂
b
=
0
,
其中
L
(
w
,
b
,
λ
)
是前面的
(
b
)
式
λ
i
≥
0
g
i
(
w
,
b
)
=
1
−
y
(
i
)
(
w
T
x
(
i
)
+
b
)
≤
0
,
i
=
1
,
2
,
.
.
.
,
n
λ
i
g
i
(
w
,
b
)
=
0
KTT条件 \left\{ \begin{array}{l} \begin{aligned}\frac{\partial L(w,b,\lambda)}{\partial w}=0, \ \frac{\partial L(w,b,\lambda)}{\partial b}=0, \ 其中L(w,b,\lambda)是前面的(b)式\end{aligned}\\[1ex] \begin{aligned}\lambda_i≥0 \end{aligned}\\[1ex] \begin{aligned}g_i(w,b)=1-y^{(i)}(w^Tx^{(i)}+b)≤0, \ i=1,2,...,n\end{aligned}\\[1ex] \lambda_ig_i(w,b)=0 \end{array} \right.
KTT条件⎩
⎨
⎧∂w∂L(w,b,λ)=0, ∂b∂L(w,b,λ)=0, 其中L(w,b,λ)是前面的(b)式λi≥0gi(w,b)=1−y(i)(wTx(i)+b)≤0, i=1,2,...,nλigi(w,b)=0
上面第4式 λ i g i ( w , b ) = 0 \lambda_ig_i(w,b)=0 λigi(w,b)=0 也称为互补条件,它表示:若 λ i > 0 \lambda_i>0 λi>0,则 1 − y ( i ) ( w T x ( i ) + b ) = 0 1-y^{(i)}(w^Tx^{(i)}+b)=0 1−y(i)(wTx(i)+b)=0,即对应的样本点 x ( i ) x^{(i)} x(i) 一定是落在间隔超平面上的支持向量;若 g i ( w , b ) < 0 g_i(w,b)<0 gi(w,b)<0,即 y ( i ) ( w T x ( i ) + b ) > 1 y^{(i)}(w^Tx^{(i)}+b)>1 y(i)(wTx(i)+b)>1 则一定有 λ i = 0 \lambda_i=0 λi=0,说明非支持向量对应的拉格朗日乘子一定为0。
因为支持向量数量较少,说明大于0的拉格朗日乘子较少,因此拉格朗日向量是一个稀疏向量。
(六)拉格朗日对偶问题及其求解
根据KKT条件第一行的求导式等于0,可得:
{
∂
L
(
w
,
b
,
λ
)
∂
w
=
w
−
∑
i
=
1
n
λ
i
y
(
i
)
x
(
i
)
T
=
0
∂
L
(
w
,
b
,
λ
)
∂
b
=
∑
i
=
1
n
λ
i
y
(
i
)
=
0
⇒
{
w
=
∑
i
=
1
n
λ
i
y
(
i
)
x
(
i
)
T
∑
i
=
1
n
λ
i
y
(
i
)
=
0
(c)式
\left\{ \begin{array}{l} \begin{aligned}\frac{\partial L(w,b,\lambda)}{\partial w}=w-\sum_{i=1}^n\lambda_iy^{(i)}x^{(i)T}=0\end{aligned}\\[2ex] \begin{aligned}\frac{\partial L(w,b,\lambda)}{\partial b}=\sum_{i=1}^n\lambda_iy^{(i)}=0\end{aligned} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \begin{aligned}w=\sum_{i=1}^n\lambda_iy^{(i)}x^{(i)T}\end{aligned}\\[2ex] \begin{aligned}\sum_{i=1}^n\lambda_iy^{(i)}=0\end{aligned} \end{array} \right.\tag*{(c)式}
⎩
⎨
⎧∂w∂L(w,b,λ)=w−i=1∑nλiy(i)x(i)T=0∂b∂L(w,b,λ)=i=1∑nλiy(i)=0⇒⎩
⎨
⎧w=i=1∑nλiy(i)x(i)Ti=1∑nλiy(i)=0(c)式
(
c
)
(c)
(c) 式带入前面的
(
b
)
(b)
(b) 式并消去
w
w
w 和
b
b
b 向量,得到只含拉格朗日乘子的损失函数:
L
(
λ
)
=
∑
i
=
1
n
λ
i
−
∑
j
=
1
n
∑
i
=
1
n
λ
i
λ
j
y
(
i
)
y
(
j
)
(
x
(
i
)
⋅
x
(
j
)
)
2
(d)式
\begin{aligned} L(\lambda)=\sum_{i=1}^n\lambda_i-\frac{\sum_{j=1}^n\sum_{i=1}^n\lambda_i\lambda_jy^{(i)}y^{(j)}\left(x^{(i)}\cdot x^{(j)}\right)}{2}\tag*{(d)式} \end{aligned}
L(λ)=i=1∑nλi−2∑j=1n∑i=1nλiλjy(i)y(j)(x(i)⋅x(j))(d)式 其中,
x
(
i
)
⋅
x
(
j
)
x^{(i)}\cdot x^{(j)}
x(i)⋅x(j) 为两个向量的内积。
由此得到拉格朗日对偶问题。该对偶问题可以用 SMO (序列最小化) 算法来高效求解。
arg min
λ
∑
i
=
1
n
λ
i
−
∑
j
=
1
n
∑
i
=
1
n
λ
i
λ
j
y
(
i
)
y
(
j
)
(
x
(
i
)
⋅
x
(
j
)
)
2
s
u
b
j
e
c
t
t
o
{
∑
i
=
1
n
λ
i
y
(
i
)
=
0
λ
i
≥
0
,
i
,
j
=
1
,
2
,
3
,
.
.
.
,
n
\begin{aligned} &\argmin_\lambda\sum_{i=1}^n\lambda_i-\frac{\sum_{j=1}^n\sum_{i=1}^n\lambda_i\lambda_jy^{(i)}y^{(j)}\left(x^{(i)}\cdot x^{(j)}\right)}{2}\\[3ex] &subject \ to \left\{ \begin{array}{l} \begin{aligned}\sum_{i=1}^n\lambda_iy^{(i)}=0\end{aligned}\\[1ex] \begin{aligned}\lambda_i≥0, \ \ i,j=1,2,3,...,n\end{aligned} \end{array} \right. \end{aligned}
λargmini=1∑nλi−2∑j=1n∑i=1nλiλjy(i)y(j)(x(i)⋅x(j))subject to⎩
⎨
⎧i=1∑nλiy(i)=0λi≥0, i,j=1,2,3,...,n
三、软间隔解决线性不可分问题
(一)软间隔SVM分类器的核心思想

软间隔SVM分类器的核心思想是允许一些样本不满足硬间隔约束/条件,即允许对一些样本犯错。
这样做是牺牲部分数据点分类准确性,来换取更宽的间隔,由此降低了模型对噪声点的敏感性,可以避免SVM分类器过拟合,提升了模型的泛化性能。
(二)软间隔SVM分类器的损失函数
arg min w , b , ξ w ⋅ w 2 + C ∑ i = 1 n ξ i s u b j e c t t o { y ( i ) ( x ( i ) w + b ) ≥ 1 − ξ i , i = 1 , 2 , 3 , . . . , n ξ i ≥ 0 \begin{aligned} &\argmin_{w,b,\xi}\frac{w\cdot w}{2}+C\sum_{i=1}^n\xi_i \\[3ex] &subject \ to \left\{ \begin{array}{l} \begin{aligned}y^{(i)}\left(x^{(i)}w+b\right)≥1-\xi_i, \ i=1,2,3,...,n\end{aligned}\\[1ex] \begin{aligned}\xi_i≥0\end{aligned} \end{array} \right. \end{aligned} w,b,ξargmin2w⋅w+Ci=1∑nξisubject to⎩ ⎨ ⎧y(i)(x(i)w+b)≥1−ξi, i=1,2,3,...,nξi≥0
软间隔有两个重要参数:
- 松弛变量 (slack variable) ξ \xi ξ,一般读作 /ksaɪ/
- 惩罚因子 (penalty parameter) C
1、松弛变量
松弛变量 ξ \xi ξ 表示样本离群的程度,松弛变量值越大,对应的样本离群越远,松弛变量为零,则对应的样本没有离群。SVM希望各样本点的松弛变量之和 ∑ i = 1 n ξ i \begin{aligned}\sum_{i=1}^n\xi_i\end{aligned} i=1∑nξi 越小越好。
2、惩罚因子
(1)惩罚因子 C 是用户设定的一个大于等于0的超参数
- C决定了你有多重视离群点带来的损失,你定的C越大,对目标函数的损失也越大,此时就暗示着你非常不愿意放弃这些离群点。
- 最极端的情况是你把C定为无限大,这样只要稍有一个点离群,目标函数的值马上变成无限大,马上让问题变成无解,这就退化成了硬间隔问题。
- 较小的C值代表着较高的容错性,此时训练误差可能会大,但泛化误差可能会小。
(2)惩罚因子对软间隔宽度和决策边界的影响

管制宽松(对应C值小),则弹性空间大,容错性高,未来可能发展得更好!
(三)核技巧使用映射函数升维解决分类问题
例1

例2
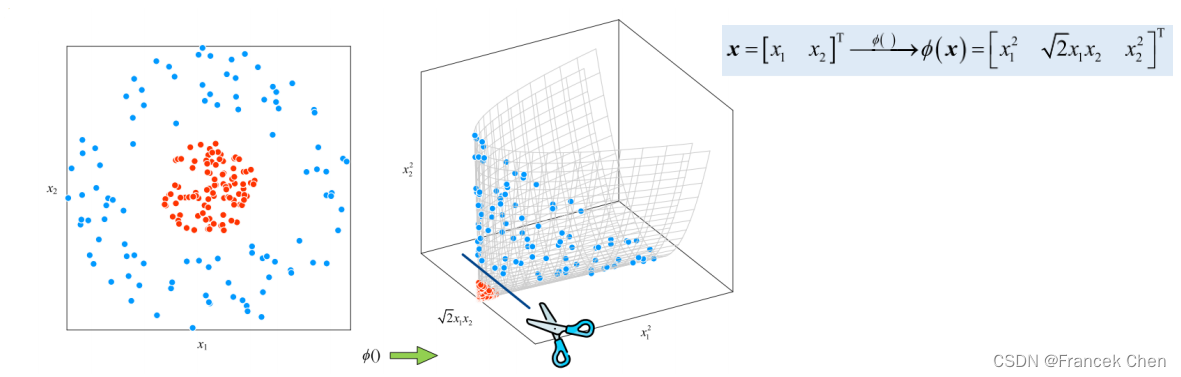
(四)软间隔+核技巧的SVM优化问题
软间隔 + 核技巧的SVM 优化问题的基本思想就是通过最小化如下的损失函数,希望在映射后的高维空间求解一个最优分类超平面:
arg min
w
,
b
w
⋅
w
2
+
C
∑
i
=
1
n
ξ
i
s
u
b
j
e
c
t
t
o
{
y
(
i
)
(
w
⋅
ϕ
(
x
(
i
)
)
+
b
)
≥
1
−
ξ
i
,
i
=
1
,
2
,
3
,
.
.
.
,
n
ξ
i
≥
0
\begin{aligned} &\argmin_{w,b}\frac{w\cdot w}{2}+C\sum_{i=1}^n\xi_i \\[3ex] &subject \ to \left\{ \begin{array}{l} \begin{aligned}y^{(i)}\left(w\cdot \phi\left(x^{(i)}\right)+b\right)≥1-\xi_i, \ i=1,2,3,...,n\end{aligned}\\[1ex] \begin{aligned}\xi_i≥0\end{aligned} \end{array} \right. \end{aligned}
w,bargmin2w⋅w+Ci=1∑nξisubject to⎩
⎨
⎧y(i)(w⋅ϕ(x(i))+b)≥1−ξi, i=1,2,3,...,nξi≥0 其中,
ϕ
(
)
\phi()
ϕ() 是映射函数。
(五)拉格朗日对偶问题与核函数
引入映射函数后的无约束拉格朗日对偶问题的形式如下:
L
(
w
,
b
,
λ
)
=
w
⋅
w
2
+
∑
i
=
1
n
λ
i
(
1
−
y
(
i
)
(
w
⋅
ϕ
(
x
(
i
)
)
+
b
)
)
=
∑
i
=
1
n
λ
i
−
∑
j
=
1
n
∑
i
=
1
n
λ
i
λ
j
y
(
i
)
y
(
j
)
ϕ
(
x
(
i
)
)
⋅
ϕ
(
x
(
j
)
)
⏞
K
e
r
n
e
l
f
u
n
c
t
i
o
n
2
\begin{aligned} L(w,b,\lambda)&=\frac{w\cdot w}{2}+\sum_{i=1}^n\lambda_i\left(1-y^{(i)}\left(w\cdot \phi\left(x^{(i)}\right)+b\right)\right)\\[3ex] &=\sum_{i=1}^n\lambda_i-\frac{\sum_{j=1}^n\sum_{i=1}^n\lambda_i\lambda_jy^{(i)}y^{(j)}\overbrace{\phi\left(x^{(i)}\right)\cdot\phi \left(x^{(j)}\right)}^{Kernel function}}{2} \end{aligned}
L(w,b,λ)=2w⋅w+i=1∑nλi(1−y(i)(w⋅ϕ(x(i))+b))=i=1∑nλi−2∑j=1n∑i=1nλiλjy(i)y(j)ϕ(x(i))⋅ϕ(x(j))
Kernelfunction
- 这里出现了两个向量映射到高维空间后的向量内积的形式
- 因为映射函数 ϕ \phi ϕ 是未知的,所以该内积无法直接计算
- 实际通过使用核函数来模拟高维空间的向量内积
核函数一般记为
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa\left(x^{(i)},x^{(j)}\right)
κ(x(i),x(j)),并且定义核函数等于高维空间的向量内积:
κ
(
x
(
i
)
,
x
(
j
)
)
=
ϕ
(
x
(
i
)
)
⋅
ϕ
(
x
(
j
)
)
\kappa\left(x^{(i)},x^{(j)}\right)=\phi\left(x^{(i)}\right)\cdot\phi \left(x^{(j)}\right)
κ(x(i),x(j))=ϕ(x(i))⋅ϕ(x(j))
(六)常见的核函数
如何选择核函数还没有统一的方法,但可以用常见的四种核函数去尝试分类。其中,线性核是支持向量机 SVM 的标配。
- 线性核 (linear kernel) : κ ( x , q ) = x ⋅ q \begin{aligned}\kappa(x,q)=x\cdot q\end{aligned} κ(x,q)=x⋅q
- 多项式核 (polynomial kernel) : κ p o l y ( d ) ( x , q ) = ( γ x ⋅ q + r ) d \begin{aligned}\kappa_{poly(d)}(x,q)=(\gamma x\cdot q+r)^d\end{aligned} κpoly(d)(x,q)=(γx⋅q+r)d
- 高斯核 (Gaussian kernel),也叫径向基核 RBF (radial basis function kernel) : κ R B F ( x , q ) = exp ( − γ ∣ ∣ x − q ∣ ∣ 2 ) \begin{aligned}\kappa_{RBF}(x,q)=\exp\left(-\gamma||x-q||^2\right)\end{aligned} κRBF(x,q)=exp(−γ∣∣x−q∣∣2)
- Sigmoid 核 (sigmoid kernel) : κ S i g m o i d ( x , q ) = tanh ( γ x ⋅ q + r ) \begin{aligned}\kappa_{Sigmoid}(x,q)=\tanh(\gamma x\cdot q+r)\end{aligned} κSigmoid(x,q)=tanh(γx⋅q+r)
以二次核为例

可以发现
ϕ
(
)
\phi()
ϕ() 映射规则并不唯一。或者说,
ϕ
(
)
\phi()
ϕ() 的具体形式并不重要,我们关心的是映射规则和标量结果。
四、scikit-learn中的SVM分类器及其主要参数
常用于构建SVM模型的类为SVC,其基本语法格式如下:
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr',
random_state=None)

(一)多分类的情形
基本思想是将多分类任务分解为多个二分类任务,对于每一个二分类任务使用一个SVM分类器。

(二)SVM的属性和方法


五、支持向量机应用示例
取自UCI公共测试数据库中的汽车评价数据集作为本例的数据集,该数据集共有6个特征数据,1个分类标签,共1728条记录,部分数据如下表所示。
| a 1 a_1 a1 | a 2 a_2 a2 | a 3 a_3 a3 | a 4 a_4 a4 | a 5 a_5 a5 | a 6 a_6 a6 | d d d |
|---|---|---|---|---|---|---|
| 4 | 4 | 2 | 2 | 3 | 2 | 3 |
| 4 | 4 | 2 | 2 | 3 | 3 | 3 |
| 4 | 4 | 2 | 2 | 3 | 1 | 3 |
| 4 | 4 | 2 | 2 | 2 | 2 | 3 |
| 4 | 4 | 2 | 2 | 2 | 3 | 3 |
| 4 | 4 | 2 | 2 | 2 | 1 | 3 |
| 4 | 4 | 2 | 2 | 1 | 2 | 3 |
| 4 | 4 | 2 | 2 | 1 | 3 | 3 |
| 4 | 4 | 2 | 2 | 1 | 1 | 3 |
| 4 | 4 | 2 | 4 | 3 | 2 | 3 |
| 4 | 4 | 2 | 4 | 3 | 3 | 3 |
| 4 | 4 | 2 | 4 | 3 | 1 | 3 |
注:数据集下载地址为:http://archive.ics.uci.edu/dataset/19/car+evaluation
数据集car.xlsx下载地址:
链接:https://pan.quark.cn/s/5c25b1f7fb08
提取码:z8Q7
其中特征 a 1 a_1 a1 ~ a 6 a_6 a6 的含义及取值依次为:
- Buying (购买价格) :v-high, high, med, low
- maint (维修成本) :v-high, high, med, low
- Doors (车门数量) :2, 3, 4, 5-more
- Persons (载客人数) :2, 4, more
- lug_boot (行李箱大小) :small, med, big
- Safety (安全等级) :low, med, high
分类标签 d d d 的取值情况为:unacc 1, acc 2, good 3, v-good 4
取数据集的前1690条记录作为训练集,余下的作为测试集,计算其预测准确率。其计算流程及思路如下:
1、数据获取
import pandas as pd
data = pd.read_excel('car.xlsx')
2、训练样本与测试样本划分。其中训练用的特征数据用x表示,预测变量用y表示;测试样本则分别记为 x 1 x_1 x1 和 y 1 y_1 y1。
x = data.iloc[:1690,:6].as_matrix()
y = data.iloc[:1690,6].as_matrix()
x1= data.iloc[1691:,:6].as_matrix()
y1= data.iloc[1691:,6].as_matrix()
3、支持向量机分类模型构建
(1)导入支持向量机模块svm。
from sklearn import svm
(2)利用svm创建支持向量机类svm。
clf = svm.SVC(kernel='rbf')
其中核函数可以选择线性核、多项式核、高斯核、sig核,分别用linear,poly,rbf,sigmoid表示,默认情况下选择高斯核。
(3)调用svm中的fit()方法进行训练。
clf.fit(x, y)
(4)调用svm中的score()方法,考查其训练效果。
rv=clf.score(x, y); # 模型准确率(针对训练数据)
(5)调用svm中的predict()方法,对测试样本进行预测,获得其预测结果。
R=clf.predict(x1)
示例代码如下:
import pandas as pd
data = pd.read_excel('car.xlsx')
x = data.iloc[:1690,:6].as_matrix()
y = data.iloc[:1690,6].as_matrix()
x1= data.iloc[1691:,:6].as_matrix()
y1= data.iloc[1691:,6].as_matrix()
from sklearn import svm
clf = svm.SVC(kernel='rbf')
clf.fit(x, y)
rv=clf.score(x, y);
R=clf.predict(x1)
Z=R-y1
Rs=len(Z[Z==0])/len(Z)
print('预测结果为:',R)
print('预测准确率为:',Rs)