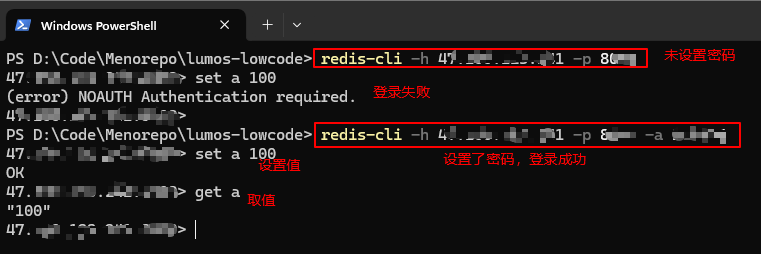
有意向获取代码,请转文末观看代码获取方式~
1 基本定义
基于EMD-PCA-LSTM的回归预测模型是一种结合了经验模态分解(Empirical Mode Decomposition, EMD)、主成分分析(Principal Component Analysis, PCA)和长短期记忆网络(Long Short-Term Memory, LSTM)的复杂回归序列预测方法。下面分别介绍这三个组成部分的基本原理以及它们是如何结合在一起的。
-
经验模态分解(EMD): EMD是一种自适应的时间序列分析方法,它能够将非线性和非平稳的时间序列分解为一系列固有模态函数(Intrinsic Mode Functions, IMFs)和一个残余项。每个IMF都是一个局部的振荡模式,并且满足两个条件:在整个数据段中,局部极大值点和局部极小值点的数目相等,且局部极大值点和局部极小值点的局部平均值是零。通过EMD分解,可以提取出时间序列中的不同频率成分,为后续分析提供基础。
-
主成分分析(PCA): PCA是一种降维技术,用于在保留数据集中大部分变异性的同时减少数据的维度。它通过正交变换将可能相关的变量转换为一组线性不相关的变量,这些不相关变量称为主成分。PCA可以提取数据中最重要的特征,减少模型的复杂度,并且有助于去除噪声。
-
长短期记忆网络(LSTM): LSTM是一种特殊的循环神经网络(RNN),它能够学习长期依赖关系。LSTM通过引入三个门(输入门、遗忘门、输出门)来控制信息的流动,从而避免传统RNN中的梯度消失或爆炸问题。LSTM非常适合处理序列数据,能够捕捉时间序列中的长期依赖关系。
结合原理:
-
首先,使用EMD对原始时间序列数据进行分解,得到多个IMFs和一个残余项。
-
然后,对这些IMFs和残余项分别应用PCA,以减少每个序列的维度并提取主要特征。
-
最后,将PCA处理后的序列作为输入,使用LSTM网络进行回归预测。
这种模型的优势在于:
-
EMD能够处理非线性和非平稳数据,提取出时间序列中的不同频率成分。
-
PCA可以进一步降低每个IMF的维度,去除噪声,提取关键特征。
-
LSTM能够学习序列数据中的长期依赖关系,进行有效的预测。
通过这三个步骤的结合,基于EMD-PCA-LSTM的回归预测模型能够处理复杂的时间序列数据,并提供准确的预测结果。
2 出图效果
附出图效果如下:
emdtest1.m运行程序后出图如下:

kpcaTest2.m运行程序后出图如下:
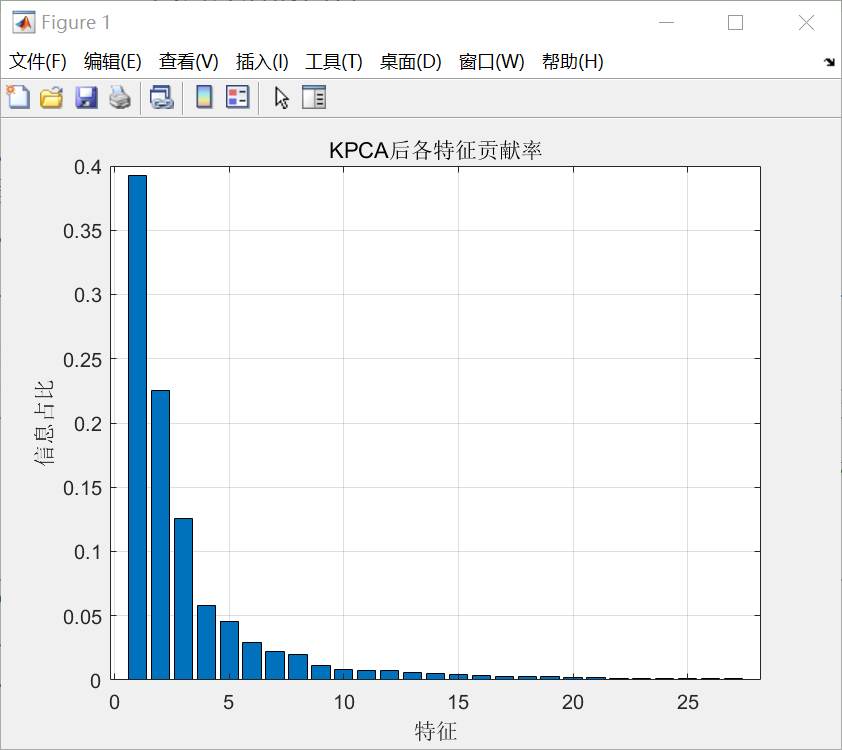
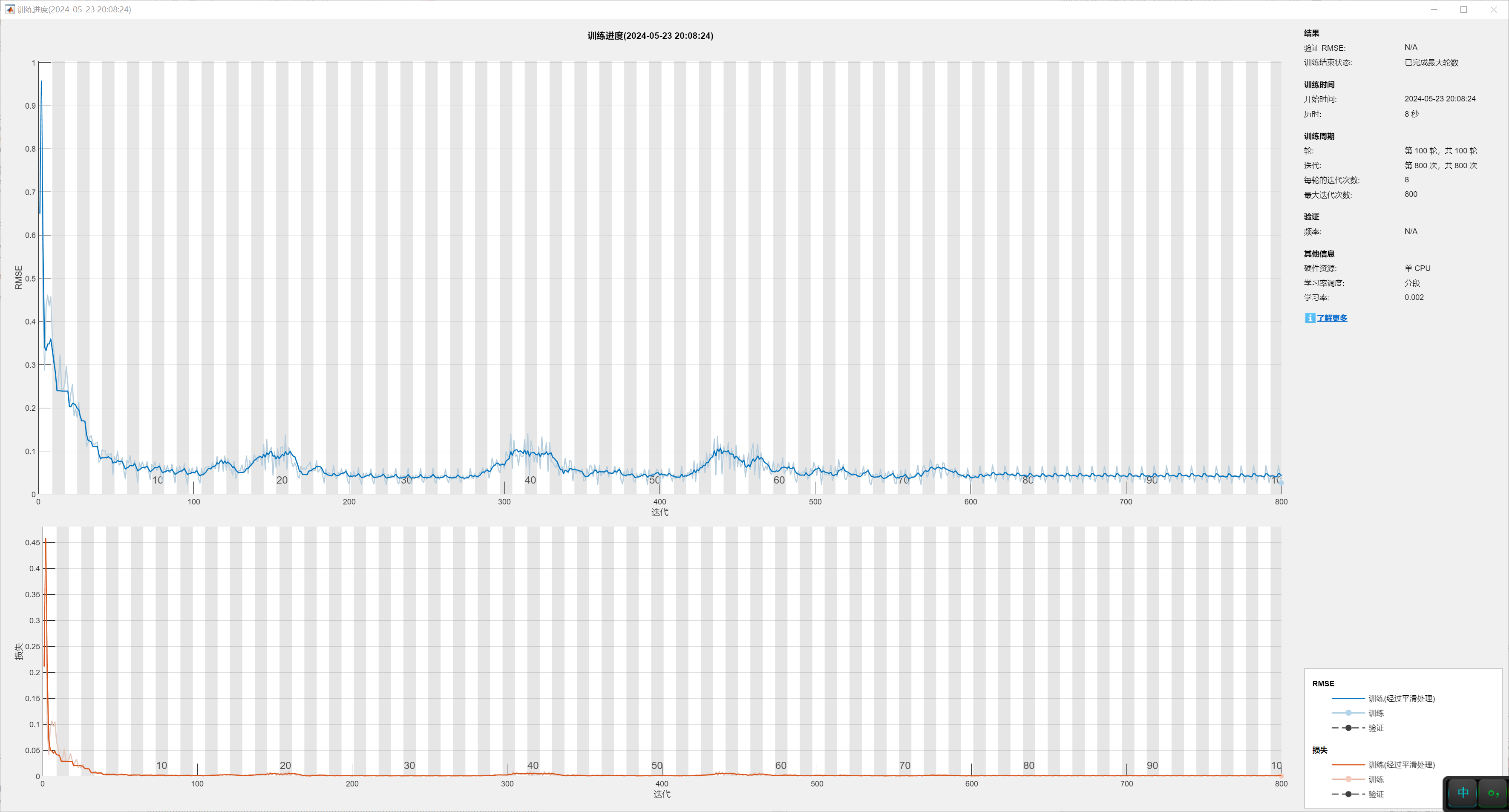
EMD_KPCA_LSTM3.m运行程序后出图如下:

附视频教程操作:
【MATLAB】基于EMD-PCA-LSTM的回归预测模型
3 代码获取
见附件~