Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting

1. 摘要

1.1 背景

交通流量预测对交通领域的研究人员和从业者来说是一个关键问题。但由于交通流量通常表现出高度的非线性和复杂的模式,因此预测非常具有挑战性。

1.2 现有方法的不足

现有的大多数交通流量预测方法缺乏对交通数据的动态时空相关性进行建模的能力,因此无法得到令人满意的预测结果。

1.3 提出的方法

本文提出了一种新颖的基于注意力机制的时空图卷积网络(ASTGCN)模型来解决交通流量预测问题。ASTGCN主要由三个独立的组件组成,分别对应于交通流量的三个时间属性:近期依赖性、日周期性依赖性和周周期性依赖性。

1.3.1 方法细节

每个组件包含两个主要部分:
(1)时空注意力机制：用于有效捕获交通数据中的动态时空相关性;
(2)时空卷积：同时采用图卷积捕获空间模式,并采用标准卷积描述时间特征。三个组件的输出进行加权融合,生成最终的预测结果。

1.4 实验结果

在来自加利福尼亚州交通运输部性能测量系统(PeMS)的两个真实数据集上进行实验,结果表明所提出的ASTGCN模型优于最先进的基准模型。

[!note]+ ASTGCN 的初印象

1. 考虑交通流量数据的三种时间依赖性:最近、日周期和周周期依赖,并为每种依赖构建独立的建模组件。
2. 每个组件包括时空注意力机制和时空卷积两个主要部分。
   • 时空注意力机制用于动态捕获交通数据的时空相关性。
   • 时空卷积同时利用图卷积捕获空间模式和普通卷积描述时间特征。
3. 三个组件的输出通过加权融合生成最终预测结果。

2 引言

2.1 研究背景

1. 智能交通系统(ITS)的发展和交通预测的重要性
2. 高速公路交通流量预测的意义

近年来,许多国家致力于大力发展智能交通系统(ITS)(Zhang et al. 2011)以助力高效的交通管理。交通预测是 ITS 不可或缺的一部分,尤其是在交通流量大、行驶速度快的高速公路上。由于高速公路相对封闭,一旦发生拥堵,将严重影响通行能力。交通流量是反映高速公路状态的基本指标。如果能够提前准确预测,交通管理部门就能据此更加合理地引导车辆,提高高速公路网络的运行效率。

2.2 问题描述

1. 高速公路交通流量预测是一个典型的时空数据预测问题
2. 交通数据在时空维度上表现出强烈的动态相关性

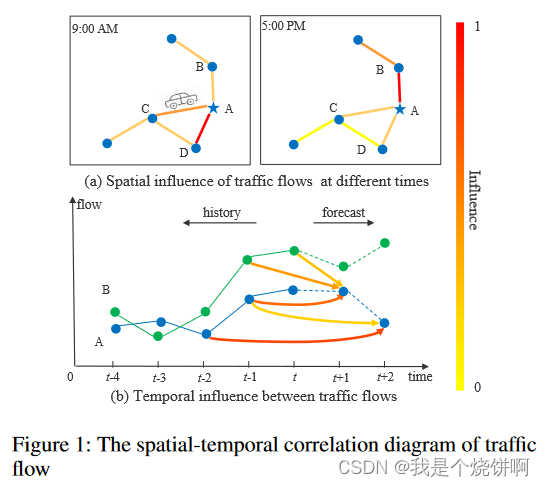
[!note]+ 图片的理解

1. 空间维度的动态相关性(图 a):
   • 不同位置(如A、B、C、D)之间存在相互影响,箭头粗细表示影响强度。
   • 同一位置(如B)在不同时间(9:00AM和5:00PM)对A的影响强度不同。
   • 这说明空间上的相关性是动态变化的,与时间相关。
2. 时间维度的动态相关性(图 b):
   • 横轴表示时间,纵轴表示交通流量。
   • 并不是一直都是时刻越接近影响就越大，对于预测 t+2 时刻反而 t-2 时刻的相关性越大

高速公路交通流量预测是一个典型的时空数据预测问题。交通数据在固定时间点和分布在连续空间中的固定位置被记录。显然,在相邻位置和时间戳记录的观测值不是独立的,而是相互之间存在动态相关性。因此,解决此类问题的关键是有效提取数据的时空相关性。

图1演示了交通流量的时空相关性(也可以是车速、车道占有率等)。两点之间的粗线表示它们的相互影响强度。线的颜色越深,影响越大。

• 在空间维度(图 a),我们可以发现不同位置对A的影响不同,即使是同一位置,随着时间的推移,对A的影响也各不相同。
• 在时间维度(图 b),不同位置的历史观测值对A在未来不同时间的交通状态有不同的影响。

总之,高速公路网络上交通数据的相关性在空间维度和时间维度都表现出强烈的动态性。如何探索非线性复杂的时空数据,发现其内在的时空模式,进行准确的交通流量预测,是一个非常具有挑战性的问题。

2.3 数据基础

1. 交通行业的发展为交通预测提供了丰富的时空数据
2. 大量富含地理信息的交通时间序列数据的积累

幸运的是,随着交通行业的发展,许多摄像头、传感器和其他信息采集设备已经部署在高速公路上。每个设备都放置在一个独特的地理空间位置,不断生成有关交通的时间序列数据。这些设备已经积累了大量富含地理信息的丰富交通时间序列数据,为交通预测提供了坚实的数据基础。

2.4 现有方法及其局限性

1. 早期的时间序列分析模型难以处理不稳定和非线性数据
2. 传统机器学习方法难以同时考虑高维交通数据的时空相关性,预测性能依赖于特征工程
3. 深度学习方法(CNN、GCN)无法同时对交通数据的时空特征和动态相关性进行建模

许多研究人员已经为解决此类问题做出了巨大努力。早期,时间序列分析模型被用于交通预测问题。然而,它们难以处理实践中不稳定和非线性的数据。后来,传统的机器学习方法被开发出来以对更复杂的数据进行建模,但它们仍然难以同时考虑高维交通数据的时空相关性。此外,这类方法的预测性能在很大程度上依赖于特征工程,这通常需要相应领域专家的大量经验。近年来,许多研究人员使用深度学习方法来处理高维时空数据,即采用卷积神经网络(CNN)来有效提取基于网格数据的空间特征;使用图卷积神经网络(GCN)来描述基于图数据的空间相关性。然而,这些方法仍然无法同时对交通数据的时空特征和动态相关性进行建模。

2.5 提出的方法

1. 基于注意力的时空图卷积网络(ASTGCN)
2. 直接在原始的基于图的交通网络上处理交通数据,有效捕获动态时空特征

为了应对上述挑战,我们提出了一种新颖的深度学习模型:基于注意力的时空图卷积网络(ASTGCN),以集体预测交通网络上每个位置的交通流量。该模型可以直接在原始的基于图的交通网络上处理交通数据,并有效捕获动态时空特征。

2.6 本文的主要贡献

1. 开发时空注意力机制学习交通数据的动态时空相关性
2. 设计新颖的时 空卷积模块对交通数据的时空依赖关系进行建模
3. 在真实世界的高速公路交通数据集上进行广泛实验,验证模型的优越性能

我们开发了一种时空注意力机制来学习交通数据的动态时空相关性。具体而言,

• 空间注意力用于建模不同位置之间复杂的空间相关性。
• 时间注意力用于捕获不同时间之间的动态时间相关性。

设计了一种新颖的时空卷积模块,用于对交通数据的时空依赖关系进行建模。它由用于从原始基于图的交通网络结构中捕获空间特征的图卷积和用于描述相邻时间片依赖关系的时间维度卷积组成。在真实世界的高速公路交通数据集上进行了广泛的实验,验证了我们的模型与现有基准相比达到了最佳的预测性能。

3 相关研究

3.1 交通预测

3.1.1 统计模型在交通预测中的应用

经过多年的持续研究和实践,交通预测领域的研究取得了许多成果。用于交通预测的统计模型包括历史平均法(HA)、自回归综合移动平均模型(ARIMA)(Williams and Hoel 2003)、向量自回归模型(VAR)(Zivot and Wang 2006)等。这些方法要求数据满足一些假设,但交通数据过于复杂,无法满足这些假设,因此它们在实践中通常表现不佳。

3.1.2 机器学习方法在交通预测中的应用

K近邻(KNN)(Van Lint and Van Hinsbergen 2012)和支持向量机(SVM)(Jeong et al. 2013)等机器学习方法可以对更复杂的数据进行建模,但它们需要仔细的特征工程。

3.1.3 深度学习在时空数据预测中的应用

由于深度学习在语音识别和图像处理等许多领域取得了突破,越来越多的研究人员将深度学习应用于时空数据预测。Zhang et al. (2018)设计了一个基于残差卷积单元的ST-ResNet模型来预测人群流量。Yao et al. (2018b)提出了一种结合卷积神经网络(CNN)和长短期记忆(LSTM)的方法来预测交通,以jointly model时空依赖性。Yao et al. (2018a)进一步提出了一种用于出租车需求预测的时空动态网络,该网络可以动态地学习位置之间的相似性。尽管这些模型可以提取交通数据的时空特征,但它们的局限性在于输入必须是标准的2D或3D网格数据。

3.2 图上的卷积

3.2.1 传统卷积的局限性

传统的卷积可以有效地提取数据的局部模式,但它只能应用于标准的网格数据。

3.2.2 图卷积的发展

最近,图卷积将传统卷积推广到图结构的数据。图卷积方法主要有两类:空间方法和谱方法。

3.2.3 空间方法

空间方法直接在图的节点及其邻居上执行卷积滤波器。因此,这类方法的核心是选择节点的邻域。Niepert, Ahmed, and Kutzkov (2016)提出了一种启发式线性方法来选择每个中心节点的邻域,该方法在社交网络任务中取得了良好的结果。Li et al. (2018)将图卷积引入人体行为识别任务。这里提出了几种划分策略,将每个节点的邻域划分为不同的子集,并确保每个节点的子集数量相等。

3.2.4 谱方法

谱方法通过谱分析来考虑图卷积的局部性。Bruna et al. (2014)提出了一种基于图拉普拉斯算子的通用图卷积框架,然后Defferrard, Bresson, and Vandergheynst (2016)通过使用切比雪夫多项式近似来实现特征值分解,对该方法进行了优化。Yu, Yin, and Zhu (2018)基于这种方法提出了一个用于交通预测的门控图卷积网络,但该模型没有考虑交通数据的动态时空相关性。

3.3 注意力机制

3.3.1 注意力机制的广泛应用

最近,注意力机制已经在自然语言处理、图像描述和语音识别等各种任务中得到广泛应用。注意力机制的目标是从所有输入中选择对当前任务相对重要的信息。

3.3.2 注意力机制在不同任务中的应用

• 图像描述任务：Xu et al. (2015)在图像描述任务中提出了两种注意力机制,并采用可视化方法直观地展示了注意力机制的效果。
• 图节点分类任务：为了对图的节点进行分类,Velickovic et al. (2018)利用自注意力层通过神经网络处理图结构数据,并取得了最先进的结果。
• 时间序列预测任务：为了预测时间序列,Liang et al. (2018)提出了一个多级注意力网络来自适应地调整多个地理传感器时间序列之间的相关性。然而,在实践中这是非常耗时的,因为需要为每个时间序列训练一个单独的模型。

3.4 研究动机

受上述研究的启发,考虑到交通网络的图结构和交通数据的动态时空模式,我们同时采用图卷积和注意力机制来对网络结构交通数据进行建模。

4 预备知识

4.1 交通网络

1. 交通网络被定义为一个无向图 $G$,包含三个要素:
   • $V$：有限的节点集合,节点数为 $N$。即 $|V|=N$
   • $E$：表示节点之间连通性的边的集合。
   • $A$：图 $G$ 的邻接矩阵,维度为 $N\times N$。
2. 交通网络 $G$ 上的每个节点以相同的频率采集 $F$ 个测量值。
3. 在每个时间片上,每个节点会生成一个长度为 $F$ 的特征向量,如图2(b)中的实线所示。

[!abstract]+ 译文
在本研究中,我们将交通网络定义为一个无向图 $G=(V,E,\mathbf{A})$,如图2(a)所示,其中 $V$ 是 $|V|=N$ 个节点的有限集合; $E$ 是一组边,表示节点之间的连通性; $\mathbf{A}\in {\mathbb{R}}^{N\times N}$ 表示图 $G$ 的邻接矩阵。交通网络 $G$ 上的每个节点以相同的采样频率检测 $F$ 个测量值,即每个节点在每个时间片上生成一个长度为 $F$ 的特征向量,如图2(b)中的实线所示。

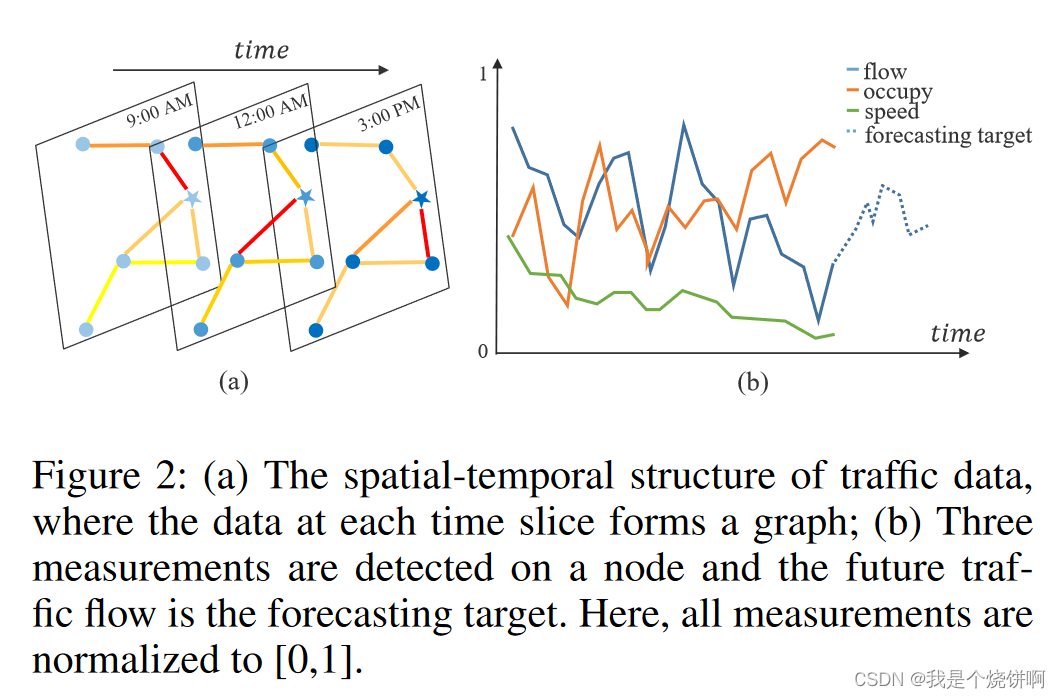
[!note]+ 说人话版本
假设我们有一个城市的交通网络,这个网络中有100个路口,每个路口都安装了传感器来采集车流量数据。

1. 节点($V$):每个路口就是网络中的一个节点,所以节点集合 $V$ 中包含100个节点。
2. 边($E$):如果两个路口之间有直接的道路连接,那么它们之间就存在一条边。边集合 $E$ 就包含了所有这些连接。
3. 邻接矩阵($A$):这是一个 $100\times 100$ 的矩阵,表示节点之间的连接关系。如果第 $i$ 个节点和第 $j$ 个节点之间有边相连,那么矩阵中的元素 $A[i,j]=1$,否则 $A[i,j]=0$。
4. 节点特征($F$):假设每个路口的传感器每隔5分钟采集一次数据,包括车流量、平均车速等多个指标。这些指标构成了该节点的特征向量,向量的长度就是指标的数量 $F$。

举个具体的例子：

如果第10号路口在早上8点采集的数据是 [车流量:100辆/5分钟,平均速度:30公里/小时] ,那么这个路口在8点这个时间片上的特征向量就是 $[100,30]$, 即 $F=2$。

所以,整个交通网络就可以用一个无向图 $G$ 来表示,图中的节点代表路口,边代表路口间的连接,邻接矩阵表示连接关系,而每个节点在每个时间片上都有一个长度为 $F$ 的特征向量。

4.2 交通流量预测

1. 交通流量预测问题的数学表示:
   • 假设第 $f$ 个时间序列是交通流量序列,其中 $f\in (1,...,F)$。
   • 使用 $x_t^{c,i}\in \mathbb{R}$ 表示节点 $i$ 在时间 $t$ 的第 $c$ 个特征值。（特定节点特定时间点特定特征）
   • 使用 ${\mathbf{x}}_t^i\in {\mathbb{R}}^F$ 表示节点 $i$ 在时间 $t$ 的所有特征值。（特定节点特定时间所有特征）
2. 定义了几个重要的张量和矩阵:
   • $({\mathbf{x}}_t^1,{\mathbf{x}}_t^2,...,{\mathbf{x}}_t^N{)}^T\in {\mathbb{R}}^{N\times F}$ 表示在时间 $t$ 所有节点的所有特征值。（所有节点特定时间所有特征）
   • $\mathcal{X}=({\mathbf{X}}_1,{\mathbf{X}}_2,{\mathbf{X}}_{\tau }{)}^{\top }\in {\mathbb{R}}^{N\times F\times \tau }$ 表示在 $\tau$ 个时间片上所有节点的所有特征值。（所有节点一段时间所有特征）
   • $y_t^i=x_t^{f,i}\in \mathbb{R}$ 表示未来时间 $t$ 节点 $i$ 的交通流量。
3. 交通流量预测问题的目标:
   • 给定 $\mathcal{X}$ (过去 $\tau$ 个时间片上所有节点的历史测量值),
   • 预测 $\mathbf{Y}=({\mathbf{y}}^1,{\mathbf{y}}^2,\dots ,{\mathbf{y}}^N{)}^{\top }\in {\mathbb{R}}^{N\times T_p}$ (未来 $T_p$ 个时间片上所有节点的交通流量),（所有节点未来一段时间单一流量特征）
   • 其中 $(y_{\tau +1}^i,y_{\tau +2}^i,...,y_{\tau +T_p}^i)\in {\mathbb{R}}^{T_p}$ 表示节点 $i$ 从 $\tau +1$ 开始的未来交通流量。（特定节点未来一段时间单一流量特征）

[!abstract]+ 译文
假设在交通网络 $G$ 中每个节点记录的第 $f$ 个时间序列是交通流量序列,其中 $f\in (1,...,F)$。
我们用 $x_t^{c,i}\in \mathbb{R}$ 表示节点 $i$ 在时间 $t$ 的第 $c$ 个特征值,
${\mathbf{x}}_t^i\in {\mathbb{R}}^F$ 表示节点 $i$ 在时间 $t$ 的所有特征值。
$({\mathbf{x}}_t^1,{\mathbf{x}}_t^2,...,{\mathbf{x}}_t^N{)}^T\in {\mathbb{R}}^{N\times F}$ 表示在时间 $t$ 所有节点的所有特征值。
$\mathcal{X}=({\mathbf{X}}_1,{\mathbf{X}}_2,{\mathbf{X}}_{\tau }{)}^{\top }\in {\mathbb{R}}^{N\times F\times \tau }$ 表示在 $\tau$ 个时间片上所有节点的所有特征值。
此外,我们设置 $y_t^i=x_t^{f,i}\in \mathbb{R}$ 表示未来时间 $t$ 节点 $i$ 的交通流量。

问题:给定 $\mathcal{X}$,即在过去 $\tau$ 个时间片上交通网络上所有节点的各种历史测量值,预测未来 $T_p$ 个时间片上整个交通网络上所有节点的未来交通流量序列 $\mathbf{Y}=({\mathbf{y}}^1,{\mathbf{y}}^2,\dots ,{\mathbf{y}}^N{)}^{\top }\in {\mathbb{R}}^{N\times T_p}$,其中 $(y_{\tau +1}^i,y_{\tau +2}^i,...,y_{\tau +T_p}^i)\in {\mathbb{R}}^{T_p}$ 表示从 $\tau +1$ 开始节点 $i$ 的未来交通流量。

说人话版本
假设我们有一个包含100个路口(节点数 N = 100)的交通网络,每个节点记录了过去1小时(τ=12个5分钟时间片)的车流量、平均速度等多个特征(假设F=2)。现在我们要预测未来15分钟(Tp=3个时间片)每个节点的车流量。
已知条件 $\mathcal{X}$:

• 维度为 100×2×12 的张量
• 包含了过去1小时内每个节点每个时间片上的2个特征值(车流量和平均速度)

目标 $\mathbf{Y}$:

• 维度为100×3 的矩阵
• 包含了未来15分钟内每个节点每个时间片上的车流量预测值

问题就变成了:给定过去1小时的交通网络状态数据 $\mathcal{X}$,预测未来15分钟每个路口的车流量 $\mathbf{Y}$。(论文只预测交通流量这一特征)

交通流量预测问题可以看作一个时空预测问题:

• 时间维度:从历史(过去 τ 个时间片)到未来(未来 Tp 个时间片)。
• 空间维度:所有节点之间的相互影响。

问题的数学表示为学习一个映射函数:

• $f$: $\mathcal{X}$ => $\mathbf{Y}$,即从历史数据预测未来流量。
• 输入 $\mathbf{X}$ 的维度为 ${\mathbb{R}}^{N\times F\times \tau }$ => 输出 $\mathbf{Y}$ 的维度为 ${\mathbb{R}}^{N\times T_p}$。

4.3 基于注意力机制的时空图卷积网络

[!info]+ [!info]+ 图注
图3展示了本文提出的ASTGCN模型的整体框架。它由三个具有相同结构的独立组件组成,分别用于对历史数据的近期、日周期和周周期依赖关系进行建模。
图3: ASTGCN的框架。SAtt:空间注意力;TAtt:时间注意力;GCN:图卷积;Conv:卷积;FC:全连接;ST block:时空块。

假设采样频率为每天 $q$ 次。假设当前时间为 $t_0$ ,预测窗口的大小为 $T_p$。如图4所示,我们沿时间轴截取三个长度分别为 $T_h$、$T_d$ 和 $T_w$ 的时间序列片段,分别作为近期、日周期和周周期组件的输入,其中 $T_h$、$T_d$ 和 $T_w$ 都是 $T_p$ 的整数倍。关于这三个时间序列片段的细节如下:

1. 近期片段：

   • ${\mathbf{X}}_h=({\mathbf{X}}_{t_0-T_h+1},{\mathbf{X}}_{t_0-T_h+2},...,{\mathbf{X}}_{t_0})\in {\mathbb{R}}^{N\times F\times T_h}$
   • 这是直接相邻于预测期的历史时间序列片段,如图4中的绿色部分所示。直观地说,交通拥堵的形成和消散是渐进的。因此,刚刚过去的交通流量不可避免地会影响未来的交通流量。

2. 日周期片段：
   $${\mathbf{X}}_d=\left({\mathbf{X}}_{t_0-\left(\frac{T_d}{T_p}\right)\cdot q+1},\cdots ,{\mathbf{X}}_{t_0-\left(\frac{T_d}{T_p}\right)\cdot q+T_p},{\mathbf{X}}_{t_0-\left(\frac{T_d}{T_p}-1\right)\cdot q+1},\cdots ,{\mathbf{X}}_{t_0-\left(\frac{T_d}{T_p}-1\right)\cdot q+T_p},\cdots ,{\mathbf{X}}_{t_0-q+1},\cdots ,{\mathbf{X}}_{t_0-q+T_p}\right)\in {\mathbb{R}}^{N\times F\times T_d}$$

   • 由过去几天与预测期相同时间段的片段组成,如图4中的红色部分所示。由于人们有规律的日常生活,交通数据可能呈现重复的模式,例如每日的早高峰。日周期组件的目的是对交通数据的日周期性进行建模。

3. 周周期片段：

   $${\mathbf{X}}_w=\left({\mathbf{X}}_{t_0-7\cdot \left(\frac{T_w}{T_p}\right)\cdot q+1},\cdots ,{\mathbf{X}}_{t_0-7\cdot \left(\frac{T_w}{T_p}\right)\cdot q+T_p},{\mathbf{X}}_{t_0-7\cdot \left(\frac{T_w}{T_p}-1\right)\cdot q+1},\cdots ,{\mathbf{X}}_{t_0-7\cdot \left(\frac{T_w}{T_p}-1\right)\cdot q+T_p},\cdots ,{\mathbf{X}}_{t_0-7\cdot q+1},\cdots ,{\mathbf{X}}_{t_0-7\cdot q+T_p}\right)\in {\mathbb{R}}^{F\times N\times T_w}$$

   • 由过去几周与预测期具有相同周属性和时间间隔的片段组成,如图4中的蓝色部分所示。通常,周一的交通模式与历史上周一的交通模式有一定的相似性,但可能与周末的交通模式有很大不同。因此,设计周周期组件是为了捕捉交通数据中的周周期特征。

这三个组件共享相同的网络结构,每个组件都由几个时空块和一个全连接层组成。在每个时空块中都有一个时空注意力模块和一个时空卷积模块。为了优化训练效率,我们在每个组件中采用了残差学习框架(He et al. 2016)。最后,三个组件的输出根据参数矩阵进一步合并,以获得最终的预测结果。整个网络结构是精心设计的,以描述交通流量的动态时空相关性。

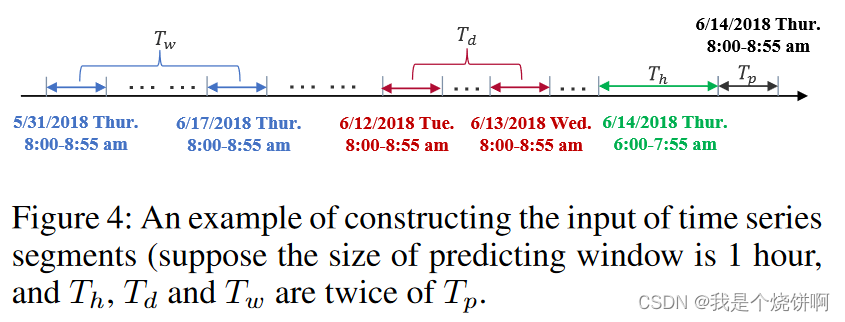
[!info]+ 图注
图 4: 这是一个构建时间序列片段输入的示例（我们假设预测窗口的尺寸为 1 小时，并且 Th、Td 和 Tw 是 Tp 的两倍）。

[!info]+ 下标解释
$t_0$ : 表示预测时段之前的最后一个历史数据点的时间戳,即 6月14日 7:55。

$t_0-q+T_p$ ：表示前一天 8:55的时间戳。

• $t_0-q$ = 6月14日 7:55 - 24 h (288 × 5) = 6月13日 7:55（前一天的同一时间点）
• $t_0-q+T_p$ ​ = 6月13日 7:55 + 12个5分钟的时间片 = 6月13日 8:55

$t_0-\left(\frac{T_d}{T_p}\right)\cdot q+T_p$ ：表示前前一天 8:55的时间戳。

• $t_0-\left(\frac{T_d}{T_p}\right)\cdot q$ = 6 月 14 日 7:55 - 2×24 h (288 × 5) = 6 月 12 日 7:55
• $t_0-\left(\frac{T_d}{T_p}\right)\cdot q+T_p$ = 6 月 12 日 7:55 + 12 个 5 分钟的时间片 = 6 月 12 日 8:55

$t_0-\left(\frac{T_d}{T_p}\right)\cdot q+1$ ：表示前前一天 8:00的时间戳。

• $t_0-\left(\frac{T_d}{T_p}\right)\cdot q$ = 6 月 14 日 7:55 - 2×24 h (288 × 5) = 6 月 12 日 7:55
• $t_0-\left(\frac{T_d}{T_p}\right)\cdot q+1$ = 6 月 12 日 7:55 + 1 个 5 分钟的时间片 = 6 月 12 日 8:00

$t_0-7\times q+T_p$：表示前一周 8:55的时间戳。

• $t_0-7\times q$ = 6 月 14 日 7:55 - 7×24 h (7×288 × 5) = 6 月 7 日 7:55
• $t_0-7\times q+T_p$ = = 6 月 7 日 7:55 + 12 个 5 分钟的时间片 = 6 月 7 日 8:55

[!note]+ 说人话版本
假设我们要预测未来1小时( Tp=12个5分钟时间片)的交通流量,当前时间是 6月14号 7:55( t0 ),采样频率为每小时 12 次,每天就是 288 次( q =288 )。

• 即 $q=288$ 、$t_0为当前时间$、$T_p=12$

1. 近期片段(绿色部分):
   • 包括上午 6:00 到 7:55 之间的交通流量数据,即从预测时段 (8:00- 8:55) 向前追溯115分钟。
   • 从 6:00 到 7:55,每5分钟采样一次,共采样24次(115分钟/5分钟+1=24)。
   • 因此,近期片段的长度 Th 为 24。
   • 整个序列 24 个元素， $t_0$ 是第 24 号，所以 $t_0-T_h+1=1$ 才能表示第 1 号元素
2. 日周期片段(红色部分):
   • 包括过去两天(6月12日和 6月13日)同一时段(上午 8:00- 8:55)的交通流量数据。
   • 每个时段采样 12 次,三天共采样 Td=2*12=24。
3. 周周期片段(蓝色部分):
   • 包括上周和上上周同一时段( 5月31日以及 6月07日星期四上午 8:00- 8:55)的交通流量数据。
   • 每个时段采样12次,因此周周期片段的长度Tw=2*12=24。

4.4 时空注意力

在我们的模型中,提出了一种新颖的时空注意力机制来捕捉交通网络上的动态空间和时间相关性(如图1所述)。它包含两种注意力,即空间注意力和时间注意力。

4.4.1 空间注意力

在空间维度上,不同位置的交通状况之间存在相互影响,而且这种相互影响是高度动态的。在这里,我们使用注意力机制(Feng et al. 2017)来自适应地捕捉空间维度中节点之间的动态相关性。以近期组件中的空间注意力为例:
$$\mathbf{S}={\mathbf{V}}_s\cdot \sigma (({\mathcal{X}}_h^{(r-1)}{\mathbf{W}}_1){\mathbf{W}}_2({\mathbf{W}}_3{\mathcal{X}}_h^{(r-1)}{)}^T+{\mathbf{b}}_s)(1)$$
其中：

• ${\mathcal{X}}_h^{(r-1)}=({\mathbf{X}}_1,{\mathbf{X}}_2,\cdots ,{\mathbf{X}}_{T_{r-1}})\in {\mathbb{R}}^{N\times C_{r-1}\times T_{r-1}}$ 是第 $r$ 个时空块的输入。
• $C_{r-1}$ 是第 $r$ 层输入数据的通道数。当 $r=1$ 时，$C_0=F$。
• $T_{r-1}$ 是第 $r$ 层的时间维度长度。当 $r=1$ 时，在近期组件中 $T_0=T_h$ (在日周期组件中 $T_0=T_d$，在周周期组件中 $T_0=T_w$)。
• ${\mathbf{V}}_s$ 和 ${\mathbf{b}}_s\in {\mathbb{R}}^{N\times N}$ 是可学习的参数。
• ${\mathbf{W}}_1\in {\mathbb{R}}^{T_{r-1}}$，${\mathbf{W}}_2\in {\mathbb{R}}^{C_{r-1}\times T_{r-1}}$，${\mathbf{W}}_3\in {\mathbb{R}}^{C_{r-1}}$ 是可学习的权重矩阵。
• $\sigma$ 是激活函数，通常使用 sigmoid 函数。

$${\mathbf{S}}_{i,j}^{\prime }=\frac{\exp ({\mathbf{S}}_{\mathrm{i},\mathrm{j}})}{{\sum }_{j=1}^N\exp ({\mathbf{S}}_{\mathrm{i},\mathrm{j}})}\text{(2)}$$
其中 $S^{\prime }$ 是归一化后的注意力矩阵，使用 softmax 函数确保每个节点的注意力权重之和为 1。矩阵 $S$ 的元素 $S_{i,j}$ 表示节点 $i$ 和节点 $j$ 之间的关联强度。

4.4.1 计算示例

假设输入数据 $X$ 为：

$$\mathcal{X}=\left(\left(\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\end{array}\right),\left(\begin{array}{cccc}2& 3& 4& 5\\ 6& 7& 8& 9\end{array}\right),\left(\begin{array}{cccc}3& 4& 5& 6\\ 7& 8& 9& 10\end{array}\right)\right)$$
这个输入张量 $\mathcal{X}$ 的形状为 $(3,2,4)$，表示有 3 个节点，每个节点有 2 个数据通道，每个通道有 4 个时间步长的数据。

假设可学习参数如下：
$$\begin{array}{c}{W}_1=\left(\begin{array}{cccc}0.1& 0.2& 0.3& 0.4\end{array}\right)\\ W_2=\left(\begin{array}{cccc}0.1& 0.2& 0.3& 0.4\\ 0.5& 0.6& 0.7& 0.8\end{array}\right)\\ W_3=\left(\begin{array}{cc}0.1& 0.2\end{array}\right)\\ V_s=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\\ b_s=\left(\begin{array}{ccc}0.1& 0.2& 0.3\\ 0.4& 0.5& 0.6\\ 0.7& 0.8& 0.9\end{array}\right)\end{array}$$
计算步骤：

1. 计算 ${\mathcal{X}}_h^{(r-1)}{W}_1$：

torch.matmul 计算后维度变化 [ 3, 2, 4 ] => [ 3, 2 ]

$${\mathcal{X}}_h^{(r-1)}{W}_1=\left(\left(\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\end{array}\right)\cdot \left(\begin{array}{c}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}\right),\left(\begin{array}{cccc}2& 3& 4& 5\\ 6& 7& 8& 9\end{array}\right)\cdot \left(\begin{array}{c}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}\right),\left(\begin{array}{cccc}3& 4& 5& 6\\ 7& 8& 9& 10\end{array}\right)\cdot \left(\begin{array}{c}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}\right)\right)$$

• 结果为：

$${\mathcal{X}}_h^{(r-1)}{W}_1=\left(\begin{array}{cc}3.0& 7.0\\ 4.0& 8.0\\ 5.0& 9.0\end{array}\right)$$

2. 计算 $({\mathcal{X}}_h^{(r-1)}{W}_1)W_2$：

$$({\mathcal{X}}_h^{(r-1)}{W}_1)W_2=\left(\begin{array}{cc}3.0& 7.0\\ 4.0& 8.0\\ 5.0& 9.0\end{array}\right)\cdot \left(\begin{array}{cccc}0.1& 0.2& 0.3& 0.4\\ 0.5& 0.6& 0.7& 0.8\end{array}\right)$$

• 结果为：

$$({\mathcal{X}}_h^{(r-1)}{W}_1)W_2=\left(\begin{array}{cccc}3.8& 4.8& 5.8& 6.8\\ 4.4& 5.6& 6.8& 8.0\\ 5.0& 6.4& 7.8& 9.2\end{array}\right)$$

3. 计算 $(W_3{\mathcal{X}}_h^{(r-1)}{)}^T$：

   torch.matmul 计算后维度变化 [ 3, 2, 4 ] => [ 3, 4 ]，4 个时间步依次做点积，2 这个维度就没有了
   $$W_3{\mathcal{X}}_h^{(r-1)}=\left(\begin{array}{ccc}\left(\begin{array}{cc}0.1& 0.2\end{array}\right)\cdot \left(\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\end{array}\right),& \left(\begin{array}{cc}0.1& 0.2\end{array}\right)\cdot \left(\begin{array}{cccc}2& 3& 4& 5\\ 6& 7& 8& 9\end{array}\right),& \left(\begin{array}{cc}0.1& 0.2\end{array}\right)\cdot \left(\begin{array}{cccc}3& 4& 5& 6\\ 7& 8& 9& 10\end{array}\right)\end{array}\right)$$

$$W_3{\mathcal{X}}_h^{(r-1)}=\left(\begin{array}{cccc}1.1& 1.4& 1.7& 2.0\\ 1.4& 1.7& 2.0& 2.3\\ 1.7& 2.0& 2.3& 2.6\end{array}\right)$$

• 结果为：

$$(W_3{\mathcal{X}}_h^{(r-1)}{)}^T=\left(\begin{array}{ccc}1.1& 1.4& 1.7\\ 1.4& 1.7& 2.0\\ 1.7& 2.0& 2.3\\ 2.0& 2.3& 2.6\end{array}\right)$$

4. 计算 $({\mathcal{X}}_h^{(r-1)}{\mathbf{W}}_1){\mathbf{W}}_2({\mathbf{W}}_3{\mathcal{X}}_h^{(r-1)}{)}^T$

$$({\mathcal{X}}_h^{(r-1)}{\mathbf{W}}_1){\mathbf{W}}_2({\mathbf{W}}_3{\mathcal{X}}_h^{(r-1)}{)}^T=\left(\begin{array}{cccc}3.8& 4.8& 5.8& 6.8\\ 4.4& 5.6& 6.8& 8.0\\ 5.0& 6.4& 7.8& 9.2\end{array}\right)\cdot \left(\begin{array}{ccc}1.1& 1.4& 1.7\\ 1.4& 1.7& 2.0\\ 1.7& 2.0& 2.3\\ 2.0& 2.3& 2.6\end{array}\right)$$

• 结果为：

$$({\mathcal{X}}_h^{(r-1)}{\mathbf{W}}_1){\mathbf{W}}_2({\mathbf{W}}_3{\mathcal{X}}_h^{(r-1)}{)}^T=\left(\begin{array}{ccc}34.36& 40.72& 47.08\\ 40.24& 47.68& 55.12\\ 46.12& 54.64& 63.16\end{array}\right)$$

[!note]+ 怎么来解释这个空间注意力
通过 $({\mathcal{X}}_h^{(r-1)}{W}_1)W_2(W_3{\mathcal{X}}_h^{(r-1)}{)}^T$ 的一系列操作，目的是生成一个 $N\times N$ 的矩阵，将各个节点各时间步综合通道特征关联起来
$$\left(\begin{array}{ccc}{N}_{1,1}& N_{1,2}& N_{1,3}\\ N_{2,1}& N_{2,2}& N_{2,3}\\ N_{3,1}& N_{3,2}& N_{3,3}\end{array}\right)$$

计算过程解析：

1. 时间特征提取 ${\mathcal{X}}_h^{(r-1)}{W}_1$：
   • ${\mathcal{X}}_h^{(r-1)}\in {\mathbb{R}}^{N\times C_{r-1}\times T_{r-1}}$ 是输入数据。
   • $W_1\in {\mathbb{R}}^{T_{r-1}}$ 是用于时间特征提取的权重。
   • 通过 ${\mathcal{X}}_h^{(r-1)}{W}_1$，我们对时间维度进行加权求和，得到每个节点在不同通道上的综合时间步特征。
2. 通道融合 $({\mathcal{X}}_h^{(r-1)}{W}_1)W_2$：
   • $W_2\in {\mathbb{R}}^{C_{r-1}\times T_{r-1}}$ 是用于通道融合的权重。将不同通道的信息进行综合处理，以获得更丰富的节点在不同时间步的特征。
   • 将时间特征表示与 $W_2$ 相乘，融合不同通道的信息，生成每个节点在不同时间步上的综合通道特征。
3. 通道特征提取 $W_3{\mathcal{X}}_h^{(r-1)}$：
   • $W_3\in {\mathbb{R}}^{C_{r-1}}$ 是用于通道特征提取的权重。
   • 通过 $W_3{\mathcal{X}}_h^{(r-1)}$，我们对通道维度进行加权求和，得到每个节点在不同时间步上的综合通道特征。
4. 关联矩阵 $({\mathcal{X}}_h^{(r-1)}{W}_1)W_2(W_3{X}_h^{(r-1)}{)}^T$：
   • $({\mathcal{X}}_h^{(r-1)}{W}_1)W_2$ 生成的矩阵表示每个节点在不同时间步上的综合通道特征。
   • $W_3{\mathcal{X}}_h^{(r-1)}$ 生成的矩阵同样表示每个节点在不同时间步上的综合特征。
   • 将 $({\mathcal{X}}_h^{(r-1)}{W}_1)W_2$ 与 $(W_3{\mathcal{X}}_h^{(r-1)}{)}^T$ 相乘，得到的结果是一个 $N\times N$ 的矩阵。这个矩阵的每个元素 $S_{i,j}$ 表示节点 $i$ 和节点 $j$ 之间的关联强度。

• 矩阵一行和一列进行计算实际上就是节点与节点之间进行点积，对节点特征向量进行点积建立关联程度（节点与节点之间建立关联）
• 节点的关联程度由 ${\mathbf{V}}_s,{\mathbf{b}}_s$ 来学习，决定各节点的关联程度