利用时间序列预测电量,冷量和压缩空气量
- 背景
- 分析与思路
- 代码
- 结果
- 一,电量预测
- 二,冷量预测
- 三,压缩空气预测
- 调优
- 一,电量预测(m=6)
- 二,冷量预测
- 三,压缩空气预测
背景
根据提供的数据,详见附件,用机器学习算法建立某工厂电量、冷量和压缩空气预测模型,并输出模型评价指标R2、RMSE、实际值与预测值对比图。(注:本次建模暂只针对用量本身,未提供其他特征变量。)
注:1、本次建模暂只针对用量本身(原始数据为表具读数,需进行计算),未提供其他特征变量,可采用时间序列方法;
2、电、冷和气原始数据内包括多个表具,其中电量由11个电表组成、冷量包括3个表具、气包括2个表具,请针对电量、冷量和压缩空气三类总用量进行建模。
分析与思路
1,由于原数据是每15分钟采集表具的,不同系统表具数目不一致,而且不同时间段的表具数目不一样,表具是随着业务一直在增加的,表具参数需要可设定;
2,由于是数据结构是不同表具不同时间点采集的,需要对原始表具读数进行计算;
3,由于原数据只提供 用量本身,未提供其他特征变量,采用时间序列方法;
4,预测的结果可以定义一个method用以评估预测结果的好坏;
代码
import time
import numpy as np
import pandas as pd
import pmdarima as pm
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score, mean_squared_error,mean_absolute_error
import warnings
warnings.filterwarnings("ignore")
warnings.simplefilter('ignore', ValueError)
import logging
logging.basicConfig(filename = 'three_predict.log', format="%(asctime)s - %(name)s - %(levelname)s - %(message)s", level=logging.DEBUG) #日志设置/app/logs/
start_time = time.time() #开始时间
class Three_Predict(object):
def __init__(self, equipment_num, windows, n_periods):
self.equipment_num = equipment_num #设备数
self.windows = windows #滑动窗口
self.n_periods = n_periods #预测期数
def fetch_data(): #读取数据
electric_data = pd.read_excel(r"D:\项目\上汽资产\算法笔试题目-上汽资产\算法笔试题目-上汽资产\预测数据集\electric.xlsx", parse_dates= [u'时间'])
cold_data = pd.read_excel(r"D:\项目\上汽资产\算法笔试题目-上汽资产\算法笔试题目-上汽资产\预测数据集\cold.xlsx", parse_dates= [u'时间'])
air_data = pd.read_excel(r"D:\项目\上汽资产\算法笔试题目-上汽资产\算法笔试题目-上汽资产\预测数据集\air.xlsx", parse_dates= [u'时间'])
print(len(electric_data), len(cold_data), len(air_data)) #, len(cold_data), len(air_data)
return electric_data
def data_preprocess(data, equipment_num, windows, n_periods): #数据预处理
print("设备数 = {}, 窗口数 = {}, 预测期数 = {}".format(equipment_num, windows, n_periods))
data_total = data.groupby(by=[u'时间']).agg({u'计量表':[len], u'表读数': [np.sum]}) #聚合
data_total.columns = [s2+'_'+s1 for s2, s1 in data_total.columns]
print(data_total)
data_total = data_total.query("计量表_len>=@equipment_num") #排除掉电表未采集到数据的情况
print(len(data_total))
data_ts = data_total[u"表读数_sum"] #电量时序
ts_rolling = data_ts.rolling(windows).mean() #阶截尾滑动平均
ts_rolling_std = ts_rolling.std() #标准差
# print("滑动平均:\n", ts_rolling, ts_rolling_std)
upper = (lambda x, y: x>y+1.5*ts_rolling_std)(data_ts, ts_rolling)
lower = (lambda x, y: x<y-1.5*ts_rolling_std)(data_ts, ts_rolling)
ts_filter = data_ts.drop(labels = data_ts[upper].index) #去上异常值
ts_filtered = ts_filter.drop(labels = data_ts[lower].index)#去下异常值
print("过滤后序列\n", ts_filtered)
y_train, y_test = ts_filtered[:-n_periods], ts_filtered[-n_periods:]
print(y_train, y_test)
return y_train, y_test
def auto_arima(data, n_periods): #auto_arima预测
model = pm.auto_arima(data,
m = 4,
seasonal = True,
trace = False,
error_action = 'ignore',
suppress_warnings = True,
stepwise = True,
n_jobs= -1) #模型初始化
print("optimum model:", model)
y_pred = model.predict(n_periods) #预测未来n_periods期
y_pred = [np.round(i) for i in y_pred] #四舍五入取整
return y_pred
def metric(y_pred, y_test): #预测结果评估
r2 = r2_score(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print("R2 = {}, RMSE = {}".format(r2, rmse))
fig = plt.figure(figsize=(8,6))
# ax = fig.add_subplot(1, 1, 1)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
print("实际值", y_test)
print("预测值", y_pred)
print(list(range(len(y_pred))))
plt.plot(y_pred, color="b", label="预测值")
plt.plot(y_test, color="g", label="实际值")
plt.legend()
plt.title("实际值与预测值对比图")
plt.show()
return r2, rmse
predict = Three_Predict(11, 4, 10)
data = Three_Predict.fetch_data()
y_train, y_test = Three_Predict.data_preprocess(data, predict.equipment_num, predict.windows, predict.n_periods)
y_pred = Three_Predict.auto_arima(y_train, predict.n_periods)
Three_Predict.metric(y_pred, y_test.tolist())
end_time = time.time() #结束时间
cost_time = end_time - start_time
print("cost time: {}".format(cost_time))
logging.info("cost time: {}".format(cost_time))
结果
一,电量预测
结果
R2 = -2.5642672586491737, RMSE = 1841.0228407056768
实际值与预测值对比图
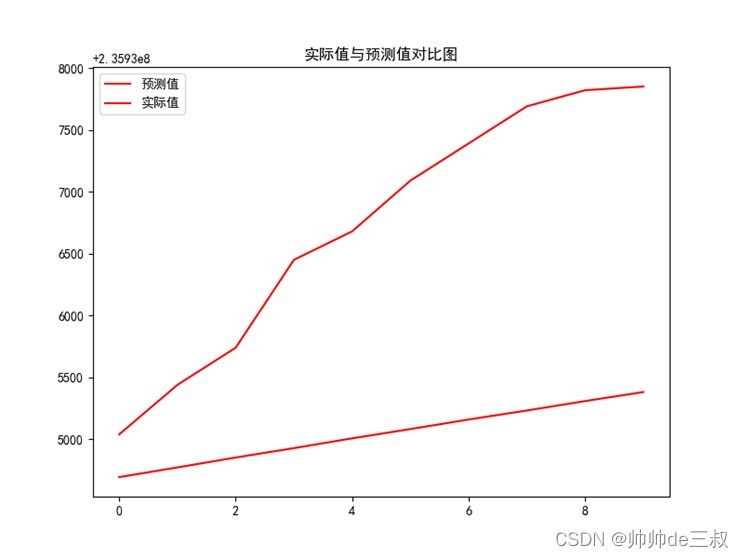
二,冷量预测
R2 = 1.0, RMSE = 0.0
实际值与预测值对比图
三,压缩空气预测
结果
R2 = -14.35457326271083, RMSE = 7931.339811154229

调优
利用时间序列建模,往往需要对参数p,d,q和周期性参数m进行调节,以达到最优,像这种工业用电,用水,用气往往具有淡旺季,一天或一周或一个月有高峰低谷的,会呈现周期性和一些趋势特点,这里重点对周期参数m进行调节
一,电量预测(m=6)
结果
R2 = 0.9306904090631372, RMSE = 256.7265081755291
实际值与预测值对比图

二,冷量预测
略
三,压缩空气预测
结果
R2 = -14.35457326271083, RMSE = 7931.339811154229