除了用于直接表示物体表面颜色，纹理的另外一种常见用法是用来进行凹凸映射，在不增加顶点的情况下，通过纹理来提供额外的法线信息，从而在视觉上增加表面凹凸细节，丰富渲染表现。

最常用的两种凹凸映射为法线贴图和高度图。

1. 法线纹理

1.1 坐标映射

法线纹理中存储的法线是经过归一化之后的值，单个分量的坐标范围为[-1, 1]。

由于颜色值的坐标范围只有[0, 1]，因此要保证能完整记录[-1, 1]的法线，就需要在存储时对法线进行坐标映射：

pixel = (normal + 1) / 2

同样，当从法线纹理中采样得到颜色值后，要得到该颜色值对应的法线信息，需要对颜色值进行一次反映射：

normal = 2 * pixel - 1

在将法线纹理导入工程时，我们可以像前文一样设置它的Texture Type为Default，此时这就是一张普通的纹理，法线的xyz对应颜色的rgb通道，在使用时，通过采样得到的rgb值按照上述反映射计算得到法线。

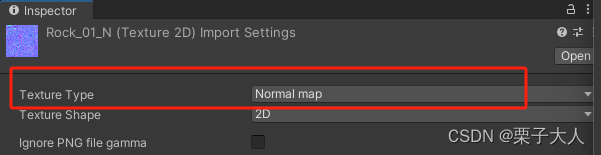
更多时候，我们会像上图这样将Texture Type设置为Normal map，此时引擎会根据平台对法线纹理进行不同的压缩，法线的xyz分量对应的有可能不再是纹理的rgb值，因此，在这种情况下，为了能够正确得到法线信息，不能再手动进行反映射计算，而是需要通过UnityGC.gcinc文件提供的 UnpackNormal(fixed4 pixel) 方法来自动进行反映射计算。

1.2 模型空间的法线纹理

模型的每个顶点都有自己对应的法线，所有这些法线都是在该模型的模型空间内，一种简单直接的方式是将修改后的法线直接存储到纹理中，生成的就是模型空间的法线纹理。

这种法线纹理的优点是简单且直观，并且由于存储的法线都处于同一个坐标空间下，因此在纹理坐标的接缝处可以对接缝两侧的法线直接进行插值计算，从而做到法线平滑过渡。

1.3 切线空间的法线纹理

实际更多使用的是切线空间的法线纹理。对于每个顶点，都存在一个独属于该顶点的切线空间，构成切线空间的三个坐标轴分别为：

• X轴：该顶点处的切线
• Z轴：该顶点处的法线
• Y轴：该顶点处的副切线（也可以叫副法线），由切线和法线叉乘获得

在导出法线纹理时，将各点处的最终法线先转换到该点的切线空间下，然后将切线空间下的法线坐标归一化并存储到纹理中，在采样时，通过该点的切线和原始法线可以构建出该点处的切线空间，再通过法线纹理的采样结果，就可以计算处该点处实际的法线，因此可以理解为，切线空间下法线纹理中记录的是每一点处的相对法线（或者叫法线的扰动）。

当某一点处的法线没有修改时，其在切线空间中的矢量应该与原始法线一致，也就是Z轴方向（0，0，1），转换为颜色值为（0.5，0.5，1），显示为淡蓝色。通常，模型中大部分法线都是没有修改的，因此往往切线空间下的法线纹理看起来都是一片蓝色。

通过切线空间来存储法线的好处最主要有两点：

• 一是由于存储的是相对法线，因此与具体模型解耦，可以方便的复用或者进行平移实现uv动画等
• 另一点是切线空间下存储的法线Z值都为正，再加上法线本身又是归一化处理之后的，那就可以通过XY的值确定Z的值，因此在存储时可以只通过两个颜色通道存储XY的值，利于压缩（相反模型空间下由于往往既有朝向Z轴正向的面又有朝向Z轴负向的面，因此模型空间下的法线的Z值也可能既有正值也有负值）

2. 使用法线纹理

以下只讨论切线空间下的法线纹理。

2.1 转换矩阵

由于纹理中记录的是切线空间中的法线，那么在进行着色时，无论是将光照等信息切换到切线空间下进行计算还是将采样得到的法线切换到世界空间下计算，首先需要确定模型空间、世界空间和切线空间的转换矩阵。

基于切线空间的定义我们得知，该空间的三条坐标轴在模型空间下的表示即为对应点的切线（Tangent_M）、副切线（BiTangent_M）和原始法线（Normal_M），那么根据前文（【Unity Shader入门精要 第4章】数学基础（二））中的内容很容易就可以构建出从切线空间到模型空间的转换矩阵为：
$$\left(\begin{array}{ccc}|& |& |\\ TangentM& BiTangentM& NormalM\\ |& |& |\end{array}\right)$$

从模型空间到切线空间的转换矩阵为：
$$\left(\begin{array}{ccc}—& TangentM& —\\ —& BiTangentM& —\\ —& NormalM& —\end{array}\right)$$

经过简单的矩阵变换，就可以得到切线空间的XYZ轴在世界空间下的表示分别为Tangent_W 、BiTangent_W 和 Normal_W ，从而可以构建出从切线空间到世界空间的转换矩阵为：
$$\left(\begin{array}{ccc}|& |& |\\ TangentW& BiTangentW& NormalW\\ |& |& |\end{array}\right)$$

以及从世界空间到切线空间的转换矩阵为：
$$\left(\begin{array}{ccc}—& TangentW& —\\ —& BiTangentW& —\\ —& NormalW& —\end{array}\right)$$

2.2 在切线空间下计算

在切线空间下计算光照时，为了节省计算量，我们可以先在顶点着色器中将计算要用到的光源方向和视角方向转换到切线空间，然后在片元着色器中与法线纹理中采样得到的法线直接进行光照计算即可。

• 创建Chapter_7_NormalMap_TagentSpace_Mat作为测试材质
• 创建Chapter_7_NormalMap_TagentSpace作为测试shader，并赋给Chapter_7_NormalMap_TagentSpace_Mat材质
• 场景中创建胶囊体，将Chapter_7_NormalMap_TagentSpace_Mat材质赋给胶囊体
• 场景中添加一盏平行光，并调整平行光角度

首先在shader中需要添加如下属性：

_BumpTex("BumpTex", 2D) = "bump"{}

该属性用于设置法线纹理，默认值为内置的bump纹理。在面板中将测试用的法线纹理赋给该属性。
同时，为了能够对设置的法线纹理正确采样，还需要声明对应的变量：

sampler2D _BumpTex;
float4 _BumpTex_ST;

为了构建旋转矩阵，在顶点着色器的输入结构中，我们需要定义一个用于接收切线数据的字段，并通过TANGENT语义通知Unity将切线信息填充到该字段。而且，该字段的类型选择为float4，主要时为了在下面构建旋转矩阵时通过其w分量来确定副切线的方向。
构建从模型空间到切线空间的旋转矩阵rotation：

float3 _bitangent = cross(normalize(v.normal), normalize(v.tangent.xyz)) * v.tangent.w;
float3x3 rotation = float3x3(v.tangent.xyz, _bitangent, v.normal);

实际上，通过UnityCG.cginc内置的宏 TANGENT_SPACE_ROTATION 可以自动为我们生成旋转矩阵rotation（名字是固定的），不需要手动计算。

最后，在片元着色器中对法线纹理采样后，通过UnpackNormal方法将颜色值反映射为法线，然后按照正常的步骤计算光照。

最终Shader如下：

Shader "MyShader/Chapter_7/Chapter_7_NormalMap_TagentSpace"
{
    Properties
    {
        _MainTex("MainTex", 2D) = "white"{}
        _BumpTex("BumpTex", 2D) = "bump"{}
        _Specular("Specular", Color) = (1,1,1,1)
        _Gloss("Gloss", Range(1.0, 256.0)) = 16
    }
    
    SubShader
    {
        Pass
        {
            Tags {"LightMode" = "ForwardBase"}
        
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            #include "UnityCG.cginc"
            #include "Lighting.cginc"
            
            struct a2v
            {
                float4 vertex : POSITION;
                float3 normal : NORMAL;
                float4 tangent : TANGENT;
                float2 uv : TEXCOORD0;
            };
            
            struct v2f
            {
                float4 vertex : SV_POSITION;
                float4 uv : TEXCOORD0;
                float3 tangentView : TEXCOORD1;
                float3 tangentLight : TEXCOORD2;
            };
            
            sampler2D _MainTex;
            float4 _MainTex_ST;
            sampler2D _BumpTex;
            float4 _BumpTex_ST;
            fixed4 _Specular;
            half _Gloss;
            
            v2f vert(a2v v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv.xy = TRANSFORM_TEX(v.uv, _MainTex).xy;
                o.uv.zw = TRANSFORM_TEX(v.uv, _BumpTex).xy;
                
//                float3 _bitangent = cross(normalize(v.normal), normalize(v.tangent.xyz)) * v.tangent.w;
//                float3x3 rotation = float3x3(v.tangent.xyz, _bitangent, v.normal);
                TANGENT_SPACE_ROTATION;
                
                o.tangentView = mul(rotation, ObjSpaceViewDir(v.vertex));
                o.tangentLight = mul(rotation, ObjSpaceLightDir(v.vertex));
                return o;
            }
            
            fixed4 frag(v2f i) : SV_Target
            {
                
                fixed3 _ambient = UNITY_LIGHTMODEL_AMBIENT.rgb;
                
                float3 _tangentLight = normalize(i.tangentLight);
                fixed4 _packedNormal = tex2D(_BumpTex, i.uv.zw);
                float3 _tangentNormal = UnpackNormal(_packedNormal);
                _tangentNormal.z = sqrt(1.0 - dot(_tangentNormal.xy, _tangentNormal.xy));
                fixed4 _albode = tex2D(_MainTex, i.uv.xy);
                fixed3 _diffuse = _LightColor0.rgb * _albode.xyz * saturate(dot(_tangentNormal, _tangentLight));
                
                float3 _tangentView = normalize(i.tangentView);
                float3 _h = normalize(_tangentView + _tangentLight);
                fixed3 _specular = _LightColor0.rgb * _Specular.xyz * pow(saturate(dot(_tangentNormal, _h)) , _Gloss);
                
                return fixed4(_ambient + _diffuse + _specular, 1);
            }
            
            ENDCG
        }
    
    }

}

效果如下：

2.3 在世界空间下计算

从纹理中采样得到的法线为切线空间下的法线，要在世界空间下进行光照计算，需要先将采样得到的法线通过变换矩阵的处理转到世界空间下，因此，我们可以在顶点着色器中通过三个float4依次记录变换矩阵的每一行，从而构建好从切线空间到世界空间的变换矩阵，同时，为了减少占用插值寄存器的数量，_worldPos的XYZ被拆分开来，分别记录到了三个float4的w分量中。

另外，这里为了跟上文中在切线空间下计算的渲染效果做对比，没有像书上一样使用Phong模型进行高光反射，依然使用的是Blinn-Phong模型，否则二者渲染出的结果差异还挺明显的。

最终Shader如下：

Shader "MyShader/Chapter_7/Chapter_7_NormalMap_WorldSpace"
{
    Properties
    {
        _MainTex("MainTex", 2D) = "white"{}
        _BumpTex("BumpTex", 2D) = "bump"{}
        _Specular("Specular", Color) = (1,1,1,1)
        _Gloss("Gloss", Range(1.0, 256.0)) = 16
    }
    
    SubShader
    {
        Pass
        {
            Tags {"LightMode" = "ForwardBase"}
        
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            #include "UnityCG.cginc"
            #include "Lighting.cginc"
            
            struct a2v
            {
                float4 vertex : POSITION;
                float3 normal : NORMAL;
                float4 tangent : TANGENT;
                float2 uv : TEXCOORD0;
            };
            
            struct v2f
            {
                float4 vertex : SV_POSITION;
                float4 uv : TEXCOORD0;
                float4 tangentToWorldX : TEXCOORD1;
                float4 tangentToWorldY : TEXCOORD2;
                float4 tangentToWorldZ : TEXCOORD3;
            };
            
            sampler2D _MainTex;
            float4 _MainTex_ST;
            sampler2D _BumpTex;
            float4 _BumpTex_ST;
            fixed4 _Specular;
            half _Gloss;
            
            v2f vert(a2v v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv.xy = TRANSFORM_TEX(v.uv, _MainTex).xy;
                o.uv.zw = TRANSFORM_TEX(v.uv, _BumpTex).xy;
                
                float3 _worldPos = mul(unity_ObjectToWorld, v.vertex);
                float3 _worldTangent = UnityObjectToWorldDir(v.tangent.xyz);
                float3 _worldNormal = UnityObjectToWorldNormal(v.normal);
                float3 _worldBitangent = cross(_worldTangent, _worldNormal) * v.tangent.w;
                
                o.tangentToWorldX = float4(_worldTangent.x, _worldBitangent.x, _worldNormal.x, _worldPos.x);
                o.tangentToWorldY = float4(_worldTangent.y, _worldBitangent.y, _worldNormal.y, _worldPos.y);
                o.tangentToWorldZ = float4(_worldTangent.z, _worldBitangent.z, _worldNormal.z, _worldPos.z);
                return o;
            }
            
            fixed4 frag(v2f i) : SV_Target
            {
                
                fixed3 _ambient = UNITY_LIGHTMODEL_AMBIENT.rgb;
                
                float3 _worldLight = normalize(_WorldSpaceLightPos0.xyz);
                fixed4 _packedNormal = tex2D(_BumpTex, i.uv.zw);
                float3 _tangentNormal = UnpackNormal(_packedNormal);
                _tangentNormal.z = sqrt(1.0 - dot(_tangentNormal.xy, _tangentNormal.xy));
                float3 _worldNormal = normalize(float3(dot(i.tangentToWorldX.xyz, _tangentNormal), dot(i.tangentToWorldY.xyz, _tangentNormal), dot(i.tangentToWorldZ.xyz, _tangentNormal)));
                fixed4 _albode = tex2D(_MainTex, i.uv.xy);
                fixed3 _diffuse = _LightColor0.rgb * _albode.xyz * saturate(dot(_worldNormal, _worldLight));
                
                float3 _worldPos = float3(i.tangentToWorldX.w, i.tangentToWorldY.w, i.tangentToWorldZ.w);
                float3 _worldView = normalize(_WorldSpaceCameraPos.xyz - _worldPos);
//                float3 _refl = normalize(reflect(-_worldLight, _worldNormal));
//                fixed3 _specular = _LightColor0.rgb * _Specular.xyz * pow(saturate(dot(_worldView, _refl)) , _Gloss);
                float3 _h = normalize(_worldLight + _worldView);
                fixed3 _specular = _LightColor0.rgb * _Specular.xyz * pow(saturate(dot(_worldNormal, _h)) , _Gloss);
                
                return fixed4(_ambient + _diffuse + _specular, 1);
            }
            
            ENDCG
        }
    
    }

}

效果如下：

3. 高度纹理

相比于记录法线，高度纹理的原理更加简单，就时直接把物体表面的起伏程度记录下来。因为只记录起伏，所以只需要一张黑白的灰度图就可以存储所需数据，其中越白的部分代表凸起程度越高。由于灰度图只能记录[0, 255]的范围，所以一般需要设置一个适当的缩放系数，从而纹理能够满足所需的数据跨度。

这是我在网上随便找的一张灰度图，通过对这张纹理进行采样，然后乘以缩放系数，既可以得到对应的起伏值，从而进行一些操作（比如生成地形）。

单纯使用灰度图的问题是，我们只能获得每个像素凸起程度的数值（或者高度值），但并不知道这个像素的法线方向，而没有法线信息就无法进行光照等着色计算。

要获得高度纹理中每个像素对应的法线信息，需要像下图一样，将纹理的类型选择为Normal map，并勾选Create from Grayscale（从灰度值生成法线），其下的两个变量Bumpiness影响凹凸程度，Filtering影响生成法线的锐利程度。

此时，Unity会根据当前灰度图自动计算每个像素位置的法线，然后将灰度图转变成一张切线空间的法线纹理，之后我们就可以像使用法线纹理一样使用这张纹理了。

当我们将这张纹理作为法线纹理对一个球体进行光照计算，于是就得到了一个奇怪的星球：