本节引入控制模型的复域模型——传递函数,并介绍其构建和使用方法。
本节介绍了几种常见环节的传递函数
文章目录
- 传递函数的定义
- 传递函数的标准形式
- 首1标准型
- 尾1标准型
- 传递函数的性质
- 传递函数的局限性
- 典型环节的传递函数
控制系统的复域数学模型是传递函数。拉普拉斯变换连接了时域与复域,因此我们使用拉氏变换来定义传递函数。
传递函数的定义
在零初始条件下,线性定常系统输出拉氏变换与输入拉氏变换之比。
「传递函数并不局限于拉氏变换之比,其他线性变换算子之比也是可以的,比如时域的微分算子D、频域的算子
j
ω
j\omega
jω,其对应的传递函数也就对应时域、频域。一般我们只讨论复域的传递函数」
G ( s ) = C ( s ) R ( s ) G(s)=\frac{C(s)}{R(s)} G(s)=R(s)C(s)
传递函数的标准形式
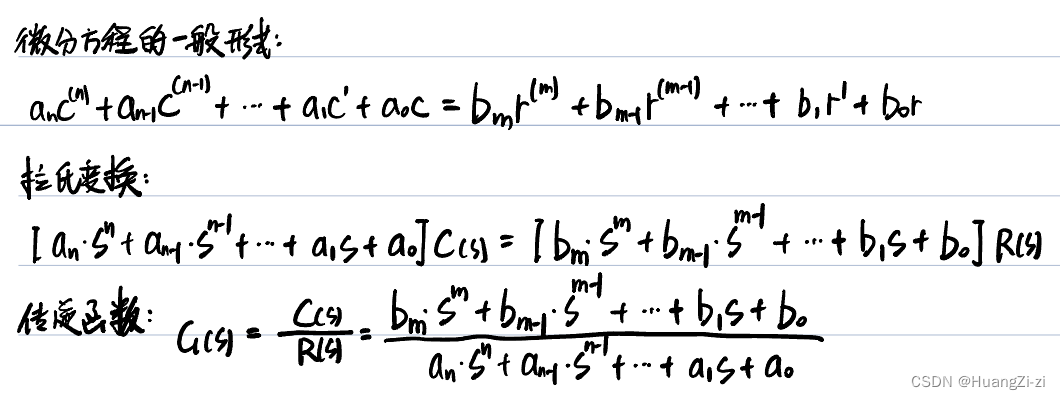
将传递函数化成标准形式,有两个化法:
首1标准型
G
(
s
)
=
K
∗
∏
j
=
1
m
(
s
−
z
j
)
∏
i
=
1
n
(
s
−
p
i
)
G(s)=\frac{K^*\prod \limits_{j=1}^m(s-z_j)}{\prod \limits_{i=1}^n(s-p_i)}
G(s)=i=1∏n(s−pi)K∗j=1∏m(s−zj)
所谓首1,就是把每一个乘积项里面s的系数化为1。
首1标准型的系数K*称为传递系数
称式中的
z
1
,
z
2
⋯
z
m
z_1, z_2 \cdots z_m
z1,z2⋯zm为传递函数的零点,当
s
=
z
j
(
j
=
1
,
2
,
⋯
m
)
s=z_j\ (j=1,2,\cdots m)
s=zj (j=1,2,⋯m)时,
G
(
s
)
=
0
G(s)=0
G(s)=0
称式中的
p
1
,
p
2
⋯
p
n
p_1, p_2 \cdots p_n
p1,p2⋯pn为传递函数的极点,使传递函数分母为零,
lim
s
→
p
j
G
(
s
)
=
∞
\lim \limits _{s\to p_j}G(s)=\infin
s→pjlimG(s)=∞
这个形式也叫做零极点形式
由于绘制根轨迹需要零极点分布,因此化成这种形式比较简单,所以系数K*也称为根轨迹增益。关于根轨迹会在后面的章节讲解。
尾1标准型
G
(
s
)
=
K
∏
k
=
1
m
1
(
τ
k
s
+
1
)
∏
l
=
1
m
2
(
τ
l
2
s
2
+
2
ξ
τ
l
s
+
1
)
s
v
∏
i
=
1
n
1
(
T
i
s
+
1
)
∏
j
=
1
n
2
(
T
j
2
s
2
+
2
ξ
T
j
s
+
1
)
G(s)=K\frac{\prod \limits_{k=1}^{m_1}(\tau_ks+1) \prod \limits_{l=1}^{m_2}(\tau_l^2s^2+2\xi \tau_ls+1)}{s^v\prod \limits_{i=1}^{n_1}(T_is+1) \prod \limits_{j=1}^{n_2}(T_j^2s^2+2\xi T_js+1)}
G(s)=Ksvi=1∏n1(Tis+1)j=1∏n2(Tj2s2+2ξTjs+1)k=1∏m1(τks+1)l=1∏m2(τl2s2+2ξτls+1)
看起来尾1要复杂得多,说白了就是把每一个乘积项里面常数项化为1。这个形式也叫做时间常数形式。
尾1标准型的系数K称为增益
在绘制Bode图时需要比较参数项与1的大小来决定近似关系,因此化成这种形式比较简单。关于Bode图会在后面的章节讲解。
看下面这个例题:

一般来说我们按照直观可以先分解出乘积项,再根据乘积项每一个因子提出一个系数,得到首1或者尾1。
传递函数的性质
- G(s)是复函数,是复变量s的有理分式
- G(s)分子阶数 ≤ \le ≤分母阶数
- G(s)只与系统自身的结构参数有关
- G(s)与系统微分方程直接关联
- G(s)= L [ k ( t ) ] \mathscr{L}[k(t)] L[k(t)],传递函数是系统单位脉冲响应的拉氏变换
- g(s)= L − 1 \mathscr{L}^{-1} L−1[G(s)],传递函数的拉氏反变换是脉冲响应
- G(s)与s平面上的零极点图相对应
零极点分布图,在s平面内,用 ∘ \circ ∘ 表示零点,用 × \times ×表示极点
极点在复平面的分布决定了系统稳定性和过渡特性。零点不影响系统稳定性,但影响暂态特性。

- 令分母多项式为零,则构成系统的特征方程,其解(极点)即为特征根,用
λ
1
、
λ
2
…
\lambda_1、\lambda_2…
λ1、λ2…表示
特征根对应的复位移称为模态,也就是 e λ 1 、 e λ 2 e^{\lambda_1}、e^{\lambda_2} eλ1、eλ2
来看一道综合性的例题:

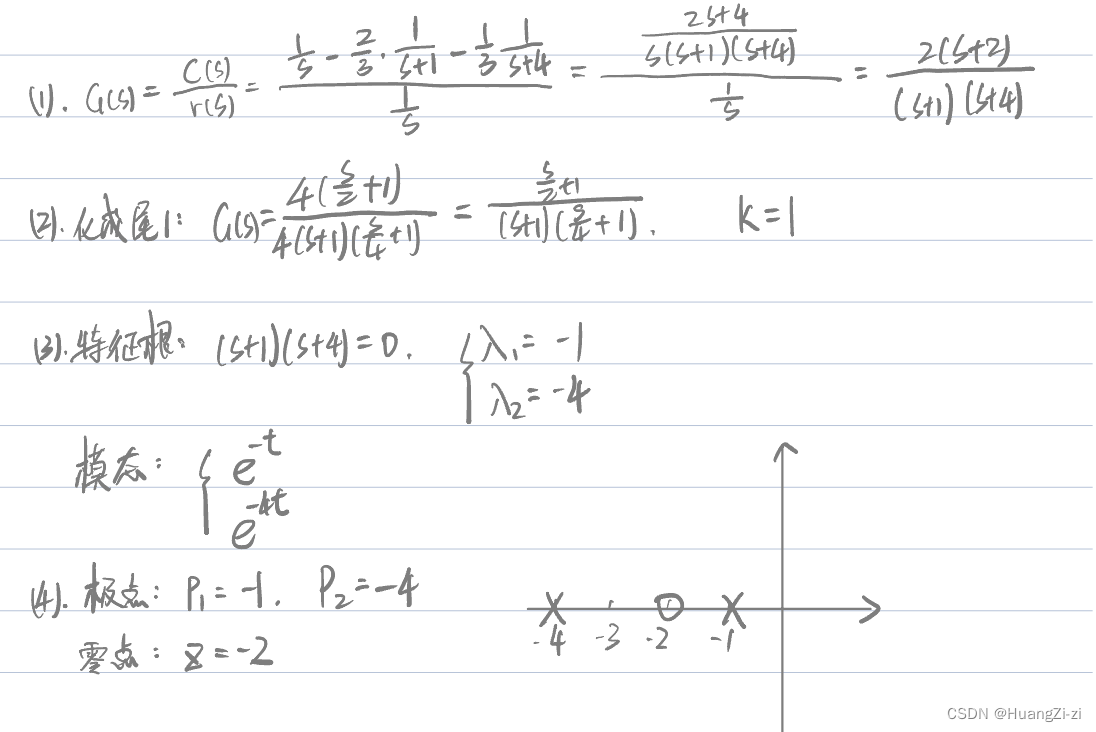

传递函数的局限性
- 对应零初始条件,原则上不反映非零初始条件时系统相应的全部信息
- 适合描述单输入、单输出系统
- 只能用于表示线性定常系统
典型环节的传递函数
环节:具有相同形式传递函数的元部件的分类
比例环节
G
(
s
)
=
K
G(s)=K
G(s)=K
典例:电位器
积分环节
G
(
s
)
=
K
s
G(s)=\frac{K}{s}
G(s)=sK
典例:液体储槽
微分环节
G
(
s
)
=
K
s
G(s)=Ks
G(s)=Ks
典例:测速发电机
纯微分环节现实中是不可实现的
惯性环节
G
(
s
)
=
K
τ
s
+
1
G(s)=\frac{K}{\tau s+1}
G(s)=τs+1K
典例:RC电路
一阶复合微分环节
G
(
s
)
=
τ
s
+
1
G(s)=\tau s+1
G(s)=τs+1
可以看作比例环节和微分环节并联
震荡环节
G
(
s
)
=
K
τ
2
s
2
+
2
ξ
τ
s
+
1
G(s)=\displaystyle \frac{K}{\tau^2s^2+2\xi \tau s+1}
G(s)=τ2s2+2ξτs+1K
二阶复合微分环节
G
(
s
)
=
τ
2
s
2
+
2
ξ
τ
s
+
1
G(s)=\tau^2s^2+2\xi \tau s+1
G(s)=τ2s2+2ξτs+1
对传递函数的解释:
- 不同元部件可以有相同的传递函数
- 选择不同的输入输出变量,同一个部件的传递函数可能不同
- 任一传递函数都可以看作典型环节的组合