随想录 && LeetCode
贪心算法
贪心之于算法,内核是一个最优解是由多个局部最优解组合而成的
比如,如何在一个月之内最有效的减肥,子问题就是每周如何减肥,再拆分就是每一天如何减肥
如果能找到令每一天都有效减肥的策略,每天都如此执行,必然就能做到一个月内有效减肥。
455 分发饼干 easy
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
子问题是如何喂饱一个孩子,全局问题是如何能喂饱更多
那用对应数量的饼干去喂对应胃口的小孩,算是如何喂饱一个孩子的策略。
这道题先考虑喂饱胃口小的,和胃口大的都可以,我选择从小的开始,代码如下:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int childIndex = 0; // 表示现在喂到了哪个娃
for (int i = 0; i < s.size(); i++) {
if (childIndex < g.size() && g[childIndex] <= s[i]) {
childIndex++;
}
}
return childIndex;
}
376 摆动序列 medium
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
这道题母的子问题是找到差值为正负交替的数字组合,全局问题是如何找到最长的数字组合。
中等难度,是因为满足条件的数组从何开始,以[1,17,5,10,13,15,10,5,16,8]为例,[1,5,10,13,15,16]是一个递增数组,摆动序列的长度就是2,这肯定没有[1, 17, 10, 13, 10, 16, 8]符合要求。
按照我们的常识,摆动的幅度越大,中间能包含的数字就越多,此处调用一张随想录中的图:
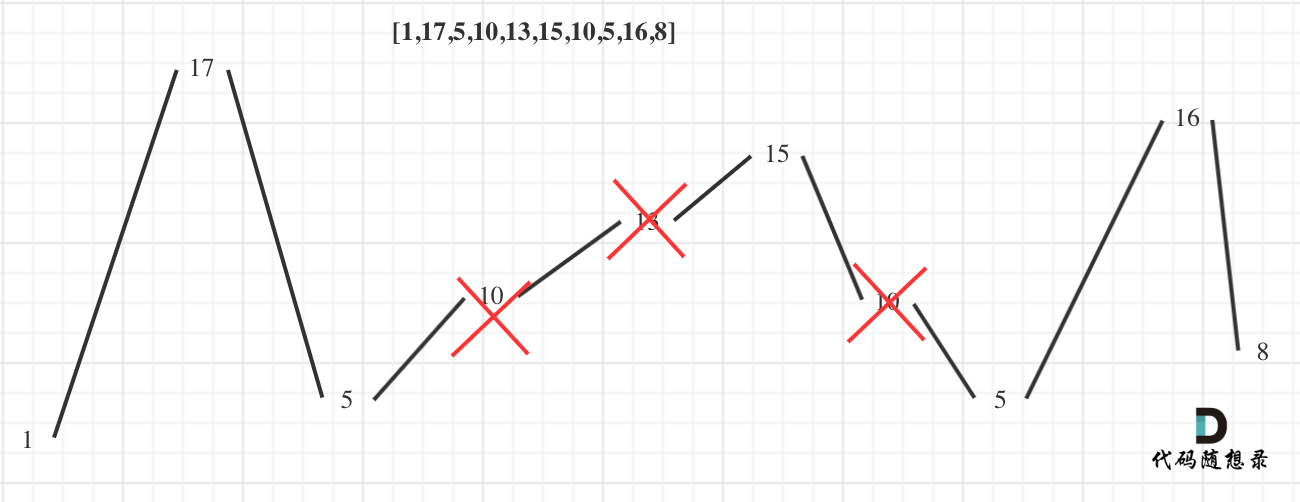
看上图,找到一个数字山脉的顶峰与低谷,就是最符合要求的解。
找顶峰与低谷,就需要判断当前一对数字的差值,和前一对数字的差值是不是符合摆动序列的要求。
整体代码如下:
int wiggleMaxLength(vector<int>& nums) {
int res = 1; //最短长度就是1
int curDiff = 0;
int preDiff = 0;
for (int i = 0; i < nums.size() - 1; ++i) {
curDiff = nums[i + 1] - nums[i];
if (curDiff < 0 && preDiff >= 0 ||
curDiff > 0 && preDiff <= 0) {
preDiff = curDiff;
res++;
}
}
return res;
}
53 最大子序和 medium
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例: 输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
本题的局部最优解是两个数字达到了最大和,此处的两个数字 = {前一对儿数字, 当前数字}
而问题就是找到最大和
按照这个思想,可以很简单的写出代码:
int maxSubArray(vector<int>& nums) {
int pre = 0, maxAns = nums[0];
for (const auto &x: nums) {
pre = max(pre + x, x);
maxAns = max(maxAns, pre);
}
return maxAns;
}
但是这个思想,也有些动态规划的感觉。
随想录中给出的想法是,序列和如果是负数,就直接从下一个数字开始考虑,前面的数字都舍弃掉
此处我多想一点,如果整个数组里都是负数,那么返回的就是其中最小的负数。
随想录中给出代码如下所示:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
result = count;
}
if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
这种解法更加符合贪心的思想。
LeetCode官方题解中,给出了一种基于分治法思想的解法,此处我们仅列出,不详细说明(因为我也还没怎么看懂)
struct Status {
int lSum, rSum, mSum, iSum;
};
Status pushUp(Status l, Status r) {
int iSum = l.iSum + r.iSum;
int lSum = max(l.lSum, l.iSum + r.lSum);
int rSum = max(r.rSum, r.iSum + l.rSum);
int mSum = max(max(l.mSum, r.mSum), l.rSum + r.lSum);
return (Status) {lSum, rSum, mSum, iSum};
};
Status get(vector<int> &a, int l, int r) {
if (l == r) {
return (Status) {a[l], a[l], a[l], a[l]};
}
int m = (l + r) >> 1;
Status lSub = get(a, l, m);
Status rSub = get(a, m + 1, r);
return pushUp(lSub, rSub);
}
int maxSubArray(vector<int>& nums) {
return get(nums, 0, nums.size() - 1).mSum;
}
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/maximum-subarray/solution/zui-da-zi-xu-he-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。