目录
1.分析下面选择题
2.实现求第n个斐波那契数
3.编写一个函数实现n的k次方,使用递归实现。
4.写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和
5.递归方式实现打印一个整数的每一位
6.实现求n的阶乘
1.分析下面选择题
根据下面递归函数:调用函数Fun(2),返回值是多少 (16)
int Fun(int n)
{
if(n==5)
return 2;
else
return 2*Fun(n+1);
}解析:当n==5的时候退出递归 先递推,再回归 n=2的时候 一直递推 到2*fun(5) 的时候结束递推(一共三次递推),然后回归(也三次) ==> 4个2相乘 =16
2.实现求第n个斐波那契数
我们要先理解什么叫斐波那契数,简单解释一下吧
1 , 1 , 2 , 3 , 5.... 那就是前两个数相加等于第三个数,例如1+1=2 1+2=3 ....
-
递归实现
假如用递归实现,要确定限制条件,那就是第一个数和第二数的时候都是返回1
Fib(1)=1,Fib(2)=1 因此我们设定条件n=1和n=2时返回1(限制条件)
而当n>=2是返回Fib (n-1)+Fib(n-2)实现递归(趋近于限制条件)
-
递归函数的缺点: 其实递归程序会不断的展开,在展开的过程中,我们很容易就能发现,在递归的过程中会有重复计算,而且递归层次越深,冗余计算就会越多。计算就会很慢
int Fib(int n) {
if (n<=2) {
return 1;
}
else
{
return Fib(n - 1) + Fib(n - 2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d", ret);
}-
迭代方式实现
-
在函数体内部,定义了三个整型变量
a、b和c,分别用于保存斐波那契数列中的相邻三个数。 -
在循环体内,
c = a + b;表示将变量c赋值为a和b的和,即斐波那契数列中的下一个数。 -
接着更新
a和b的值,将a更新为原来的b,将b更新为原来的c,以便下一次迭代计算。
int Fib(int n) {
int a = 1;
int b = 1;
int c = 1;
while (n>2)
{
c = a + b; //
a = b;
b = c;
n--;//减到<=2的时候退出循环
}
return c;
}
int main() {
int n = 0;
scanf("%d", &n);
int r = Fib(n);
printf("%d\n", r);
return 0;
}3.编写一个函数实现n的k次方,使用递归实现。
-
思考一下,什么是限制条件?
-
当指数k一直减减减到为0的时候,那么结果返回1,结束递归
-
power(n, k - 1): 这部分是递归调用,它会计算n的k - 1次方。这就是递归的关键,它通过反复调用自身来逐步减小问题的规模。 -
n * power(n, k - 1): 这里将n与n的k - 1次方相乘,从而得到n的k次方。因为n的k次方可以表示为n乘以n的k - 1次方。
#include <stdio.h>
// 递归函数计算n的k次方
double power(double n, int k) {
// 递归基
if (k == 0)
return 1;
// 若k为负数,则返回1除以n的-k次方
if (k < 0)
return 1 / power(n, -k);
// 递归计算n的k次方
return n * power(n, k - 1);
}
int main() {
double n;
int k;
printf("请输入底数n和指数k:");
scanf("%lf%d", &n, &k);
double result = power(n, k);
printf("%.2lf的%d次方为%.2lf\n", n, k, result);
return 0;
}4.写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和
例如,调用DigitSum(1729),则应该返回1+7+2+9,它的和是19
输入:1729,输出:19
int DigitSum(int n)
{
if (n < 10)
return n;
else
{
int sum = n % 10 + DigitSum(n / 10);
return sum;
}
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d", DigitSum(n));
return 0;
}
5.递归方式实现打印一个整数的每一位
-
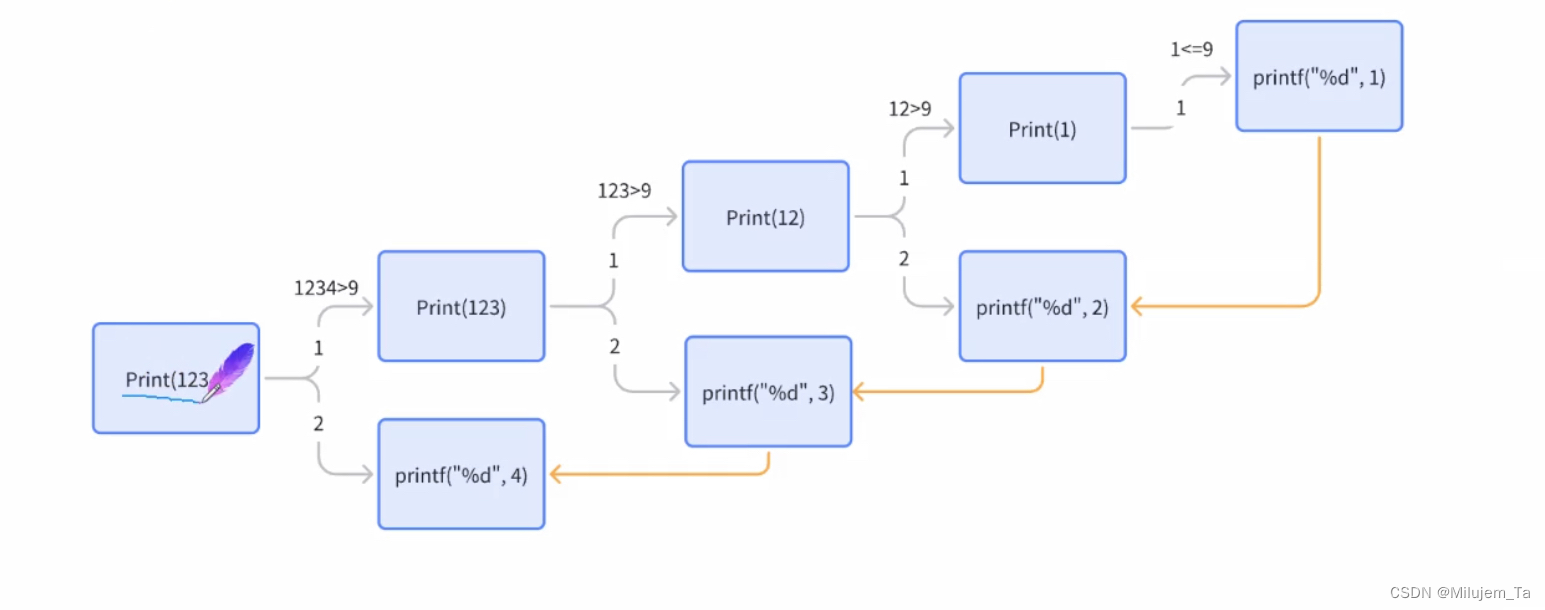
分析:用递归的方法 我们将 1234 按顺序输出 1 2 3 4
我们可以定义一个Print()函数
先递推:(一直递推到最高位,然后再从最高位开始打印,就会按顺序输出)
(1234) 除以十去掉最后一位 (123) 4
(123) 4 ---> (12) 3 4 ----> (1)2 3 4 ---> 1 2 3 4
每次都调用自己,直到不能再分(限制条件)
后回归:
-
最后当n=1的时候不满足n>9的条件,达到限制条件然后进行回归,
1%10 = 1
12%10=2
123%10 =3
然后再顺序输出1 2 3
int Print(int n) {
if (n > 9)//当n是两位数以上
{
Print(n / 10);
}
printf("%d ", n % 10);
}
int main() {
int n = 0;
scanf("%d", &n);
Print(n);
}6.实现求n的阶乘
递归和非递归分别实现(不考虑溢出的问题)
-
递归的方法
-
当n=0的时候 阶层为1 ==>限制条件
-
不等于0的时候就算阶层
//递归方式
int Fact(int n) {
if (0 == n) {
return 1;
}
else
{
return n * Fact(n - 1);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = Fact(n);
printf("%d", ret);
return 0;
}-
非递归方法
int Fact(int n) {
int sum = 1;
int i = 0;
for (i = 1; i <= n; i++) {
sum *= i;
}
return sum;
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = Fact(n);
printf("%d", ret);
return 0;
}