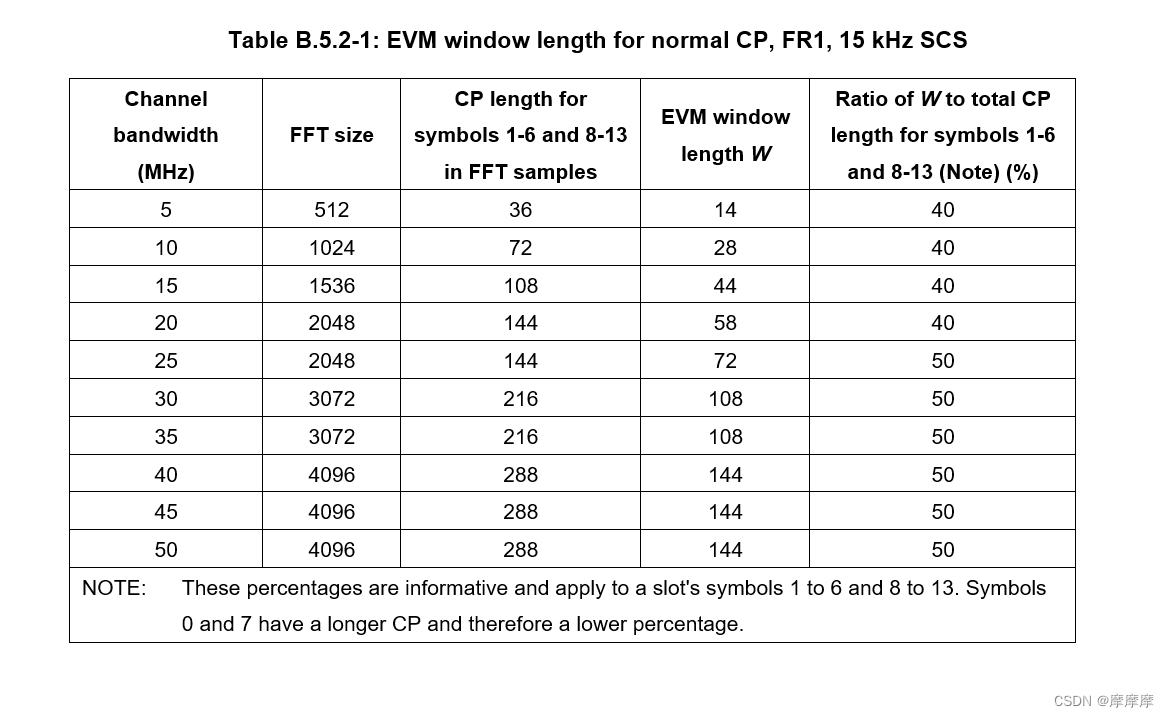
前置知识:
- 树形结构
- 链式前向星(熟练)
- 线段树(熟练)
- DFS序(熟练)
- LCA(了解定义)
什么是树链剖分
树链剖分其实有两种:重链剖分和长链剖分。重链剖分就是把儿子节点最重的儿子称为重儿子,把树分成若干条重链(如图一);
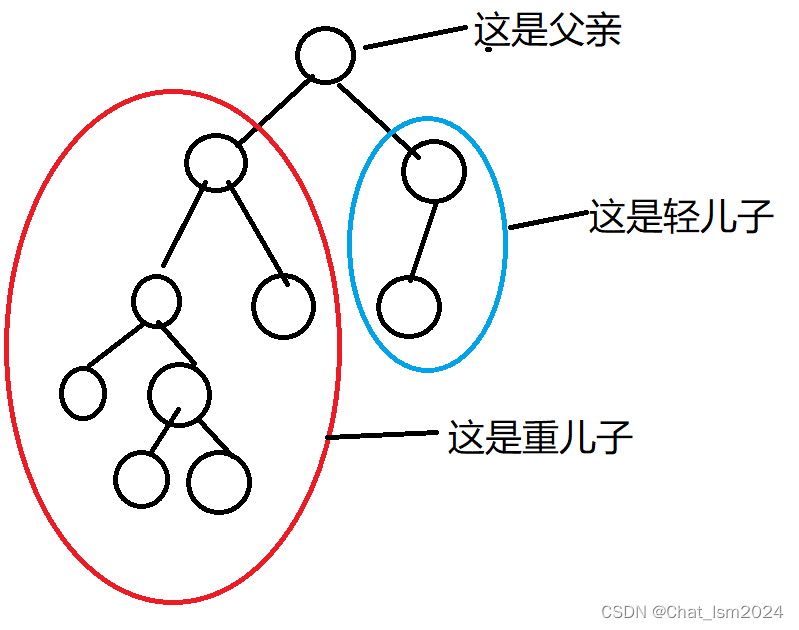
长链剖分则是把深度差最大的儿子称为长儿子,把树分成若干条长链(如图二):
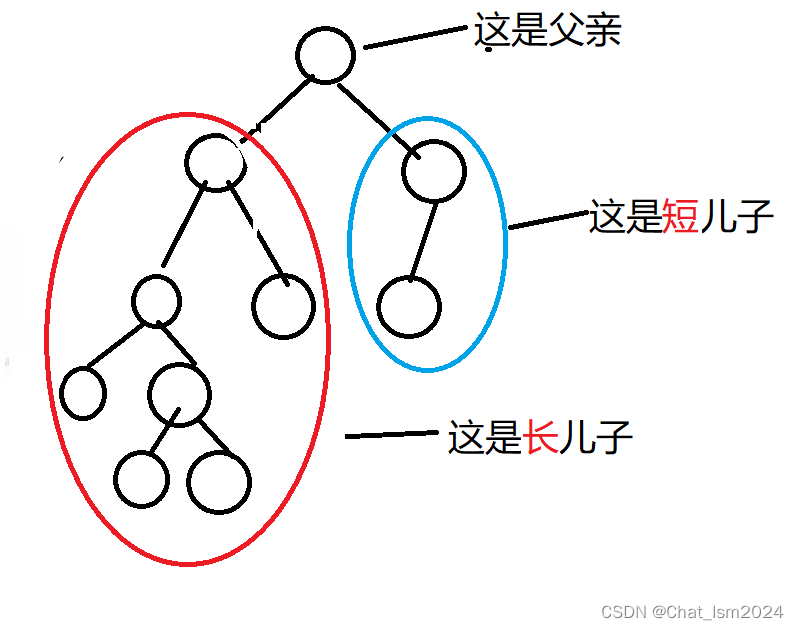
树链剖分的应用非常广泛,一般用的都是重链剖分。
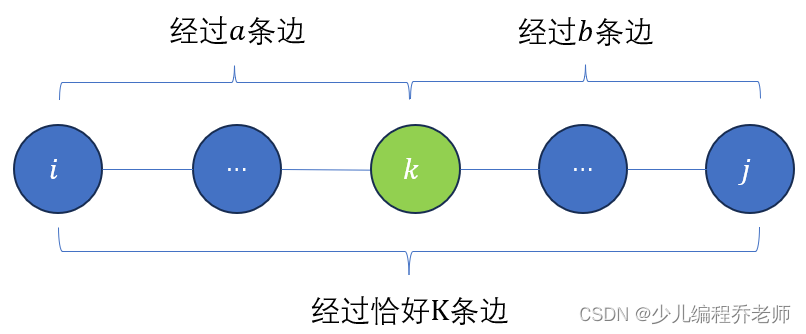
树链剖分是提高树上搜索效率的一个巧妙方法,它一定规则把树剖分成一条线性的不相交的链,对整棵树的操作,就转化为对链的操作;而从根到任何一条链只是经过条链从而操作的复杂度为
。
树链剖分的一个特别之处,就是每条链的 DFS序 是有序的可以使用线段树处理,从而高效地解决一些树上的修改和查询问题。
树链剖分和LCA
首先通过求最近公共祖先介绍树链剖分的基本概念,而且进行树链剖分时求 LCA 是必需的步骤。
LCA 的概念
- LCA问题:在一棵有根树中,一个节点的祖先节点是指它本身或者它父节点的祖先。给定两个节点,两个点共同的祖先中距离两者最近的节点就是这两个节点的最近公共祖先。需要注意的是最近公共祖先可能是这两个节点中的某一个。
- 求LCA的各种算法都是快速向上“跳”到祖先节点。回顾求LCA的两种方法,其思想可以概括为:①倍增法,用二进制递增直接向祖先“跳”;②Tarjan算法,用并查集合并子树,子树内的节点都指向子树的根,查询LCA时,可以从节点直接跳到它所在的子树的根,从而实现快速跳的目的。
树链剖分的基本概念:
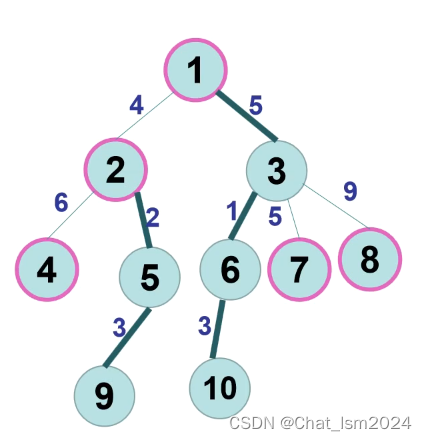
- 重儿子:假设x有n个儿子节点,其中以3儿子节点的为根子树大小最大,3就是x的重儿子
- 轻儿子:除重儿子外的所有儿子均为轻儿子
- 以图三为例:1的重儿子为3,轻儿子为2;3的重儿子为6,其余的为轻儿子
- 轻边:x与轻儿子相连的边
- 重边:x与重儿子相连的边
- 轻链:均由轻儿子构成的一条链
- 重链:均由重儿子构成的一条链
进行树链剖分时,求 LCA也是必需的步骤。 和倍增法很像,树链剖分也是“跳”到祖先节点,它的跳法比较巧妙。每条链路内的节点可以看作一个集合,并以“链头”为集;链路上的节点查询LCA时,都指向链头,从而实现快速跳的目的。特别关键的是,从根到叶子只需要经过条链,那么从一个节点跳到它的LCA,只需要跳
条链。
如何把树剖成链,使从根到叶子经过的链更少?注意每个节点只能属于一条链。很自然的思路是观察树上节点的分布情况,如果选择那些有更多节点的分支建链,链会更长一些,从而使链的数量更少。如图四所示,图四从根节点a开始,每次选择有更多子节点的分支建链,最后形成了粗线条所示的3条链。从叶子节点到根,最多经过两条链。例如,从 h 到 a,先经过以 d 为头的链,然后就到了以 a 为头的链。

预处理节点信息
我们需要的信息如下
- dep[X]:x节点的深度
- fa[X]:x节点的父亲节点
- son[X]:x节点的重儿子
- siz[X]:x节点为根的子树大小
- top[X]:x节点所在链的顶点
首先第一个DFS我们直接获取 dep[X],fa[X],son[X],siz[X]
void dfs1(int x) {
siz[x] = 1;
dep[x] = dep[f[x]] + 1;
for (int i = head[x]; i; i = e[i].ne) {
int dd = e[i].to;
if (dd == f[x])continue;
f[dd] = x;
dfs1(dd);
siz[x] += siz[dd];
if (!son[x] || siz[son[x]] < siz[dd])
son[x] = dd;
}
}接下来获取top[X]
我们处理的方式:优先对重儿子处理,重儿子处理结束后再处理轻儿子(新开链)
void dfs2(int x, int tv) {
top[x] = tv;
if (son[x])dfs2(son[x], tv);
for (int i = head[x]; i; i = e[i].ne) {
int dd = e[i].to;
if (dd == f[x] || dd == son[x])continue;
dfs2(dd, dd);
}
}现在,我们按照倍增法求LCA的思路推导,看看能不能转化到树链剖分上。
经过剖分得到重链后,该怎么求 x,y 的LCA呢?有两种情况:
- 当两个节点在同一条重链上的时候。重链上的节点都是祖先和后代的关系,所以位置就在深度最浅的那个节点上。
- x和y不在同一条重链上。让x和y沿着这一条重链向上条,直到位于同一条重链,此时直接向上跳即可。
好了,现在我们掌握了精髓,代码如下(是不是很简单?):
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
while (top[x] != top[y]) {
if (dep[top[x]] >= dep[top[y]])x = f[top[x]];
else y = f[top[y]];
}
printf("%d\n", dep[x] < dep[y] ? x : y);
}完整代码(洛谷P3379)
//来自于https://www.luogu.com.cn/problem/P3379
#include <cstdio>
#include <iostream>
using namespace std;
struct edge {
int to, ne;
} e[1000005];
int n, m, s, ecnt, head[500005], dep[500005], siz[500005], son[500005], top[500005], f[500005];
void add(int x, int y) {
e[++ecnt].to = y;
e[ecnt].ne = head[x];
head[x] = ecnt;
}
void dfs1(int x) {
siz[x] = 1;
dep[x] = dep[f[x]] + 1;
for (int i = head[x]; i; i = e[i].ne) {
int dd = e[i].to;
if (dd == f[x])continue;
f[dd] = x;
dfs1(dd);
siz[x] += siz[dd];
if (!son[x] || siz[son[x]] < siz[dd])
son[x] = dd;
}
}
void dfs2(int x, int tv) {
top[x] = tv;
if (son[x])dfs2(son[x], tv);
for (int i = head[x]; i; i = e[i].ne) {
int dd = e[i].to;
if (dd == f[x] || dd == son[x])continue;
dfs2(dd, dd);
}
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 1; i < n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
dfs1(s);
dfs2(s, s);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
while (top[x] != top[y]) {
if (dep[top[x]] >= dep[top[y]])x = f[top[x]];
else y = f[top[y]];
}
printf("%d\n", dep[x] < dep[y] ? x : y);
}
}典型应用
关于重链,还有一个重要特征没有提到:一条重链内部节点的DFS序(时间戳)是连续的。也就是说,如果用DFS序标记这条重链上的节点,那么这条重链就变成一段连续的数字。把这段连续的数字看作“线段”,线段内的区间问题用线段树处理正合适。
根据上述讨论,能够用数据结构(一般是线段树)维护重链,从而高效解决一些树上的问题,如以下问题。
- 修改点x到点y的路径上各点的权值。
- 查询点x到点y的路径上节点权值之和。
- 修改点x子树上各点的权值。
- 查询点x子树上所有节点的权值之和。
其中,问题(1)是“树上差分”问题,详见前面的“倍增+差分”解法。树上差分只能解决简单的修改问题,对问题(3)这样的修改整棵子树的问题,树上差分就行不通了。
1.重链的DFS序(时间戳)
前面给出的dfs2()函数,是先DFS重儿子,再DFS轻儿子。如果在dfs2()函数的第1句用编号记录节点x的DFS序,即
,对每个节点重新编号的结果如图4.50所示。
观察到以下现象。
部节点的编号是有序的。重链的DFS序是
;重链
的DFS序是
;重链
的DFS序是
。

(2)每棵子树上的所有节点的编号也是有序的。例如,以为根的子树
,其DFS序是
。
下面是关键内容-用线段树处理重链。由于每条重链内部的节点是有序的,可以按DFS序把它们安排在一棵线段树上。把每条重链看作一个连续的区间,对一条重链内部的修改和查询,用线段树处理;若一条路径跨越了多条重链,简单地跳过两条重链之间的轻边即可。
提示
重链内部用线段树,重链之间跳过。
如图4.51所示,先建一棵线段树,然后把线段树的节点看作DFS序(时间戳)。DFS序对应了原来那棵树的节点。同一条重链的节点,在线段树上是连续的。
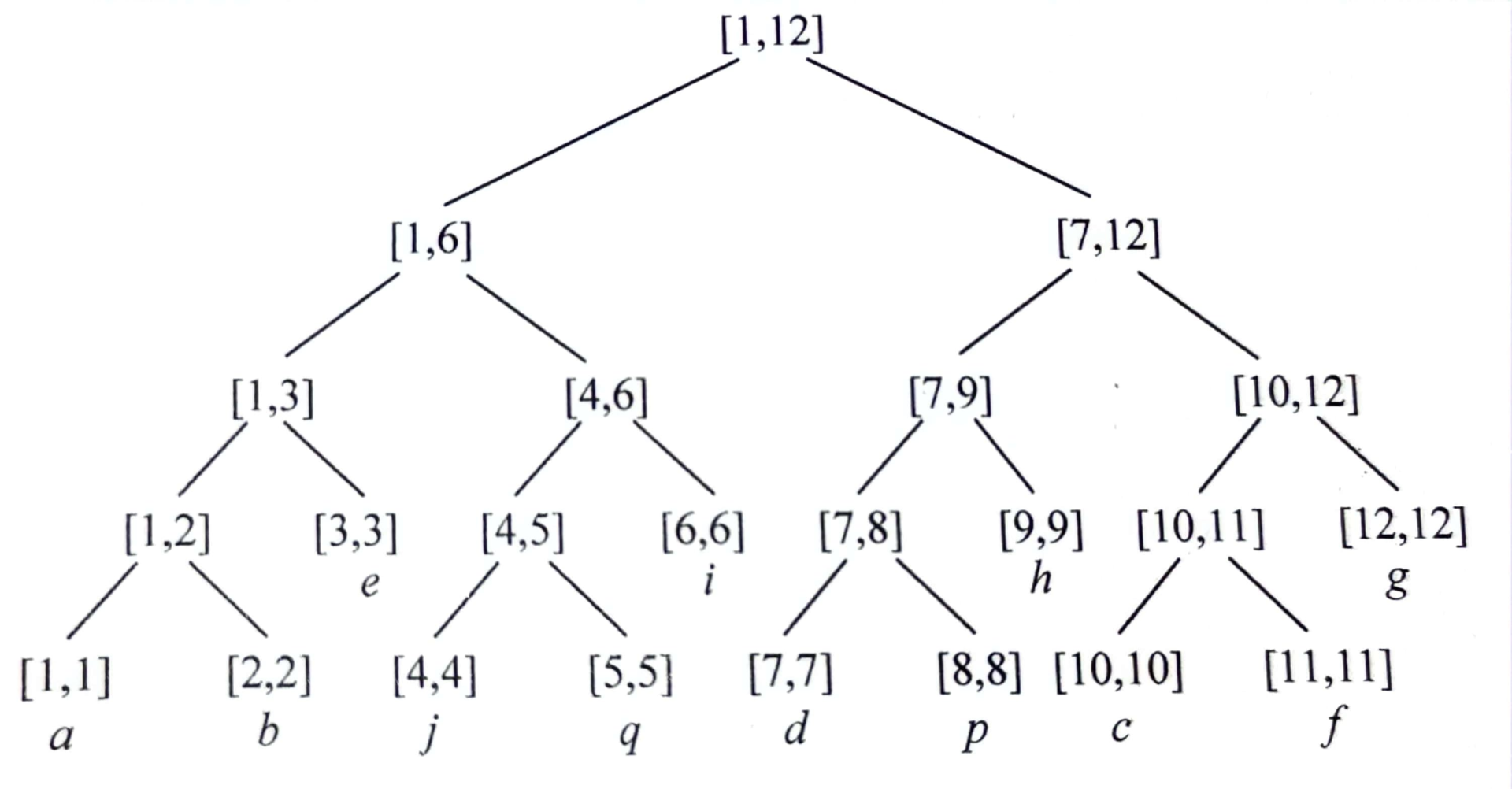
2.修改x到y的最短路径上的节点权值
x到y的最短路径经过,这实际上是一个查找
的过程。可以借助重链修改路径上的节点权值,步骤如下。
- 令x的链头的深度更深,即
。从x开始向上走,先沿着x所在的重链向上走,修改这一段路径上的节点。
- 到达x的链头后,跳过一条轻边,到达上一条重链。
- 继续执行步骤(1)和步骤(2),直到x和y位于同一条重链上,再修改此时两点之间的节点。
例如,修改从p到q的路径上所有节点权值之和,步骤如下。
- 从p走到它的链头
,修改p和d的权值。
- 跳到b。
- b和q在同一条重链上,修改从b到q的权值。
用线段树处理上述过程,仍以修改从p到q的路径上节点权值之和为例。
- 从p跳到链头
和d属于同一条重链,用线段树修改对应的
区间。
- 从d穿过轻边
,到达b所在的重链。
- b和q在同一条重链上,用线段树修改对应区间
。
3.查询x到y的路径上所有节点权值之和
查询与修改的过程几乎一样,以查询p到q的路径上节点权值之和为例。
- 从p跳到链头d,p和d属于同一条重链,用线段树查询对应的[7,8]区间;
- 从d穿过轻边(b,d),到达b所在的重链;
- b和q在同一条重链上,用线段树查询对应区间[2,5]。
4.修改x的子树上各点的权值,查询x的子树上节点权值之和
每棵子树上的所有节点的DFS序是连续的,也就是说,每棵子树对应了一个连续的区间。
例题——洛谷P3384 轻重链剖分
题目描述
如题,已知一棵包含 NN 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
1 x y z,表示将树从 xx 到 yy 结点最短路径上所有节点的值都加上 zz。
2 x y,表示求树从 xx 到 yy 结点最短路径上所有节点的值之和。
3 x z,表示将以 xx 为根节点的子树内所有节点值都加上 zz。
4 x表示求以 xx 为根节点的子树内所有节点值之和输入格式
第一行包含 44 个正整数 N,M,R,PN,M,R,P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 NN 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N-1N−1 行每行包含两个整数 x,yx,y,表示点 xx 和点 yy 之间连有一条边(保证无环且连通)。
接下来 MM 行每行包含若干个正整数,每行表示一个操作。
输出格式
输出包含若干行,分别依次表示每个操作 22 或操作 44 所得的结果(对 PP 取模)。
输入输出样例
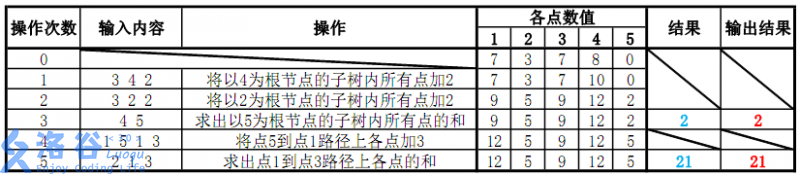
输入 #1复制
5 5 2 24 7 3 7 8 0 1 2 1 5 3 1 4 1 3 4 2 3 2 2 4 5 1 5 1 3 2 1 3输出 #1复制
2 21说明/提示
【数据规模】
对于 30\%30% 的数据: 1 \leq N \leq 101≤N≤10,1 \leq M \leq 101≤M≤10;
对于 70\%70% 的数据: 1 \leq N \leq {10}^31≤N≤103,1 \leq M \leq {10}^31≤M≤103;
对于 100\%100% 的数据: 1\le N \leq {10}^51≤N≤105,1\le M \leq {10}^51≤M≤105,1\le R\le N1≤R≤N,1\le P \le 2^{30}1≤P≤230。所有输入的数均在
int范围内。【样例说明】
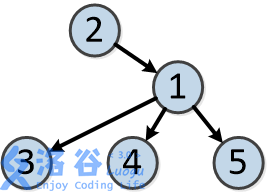
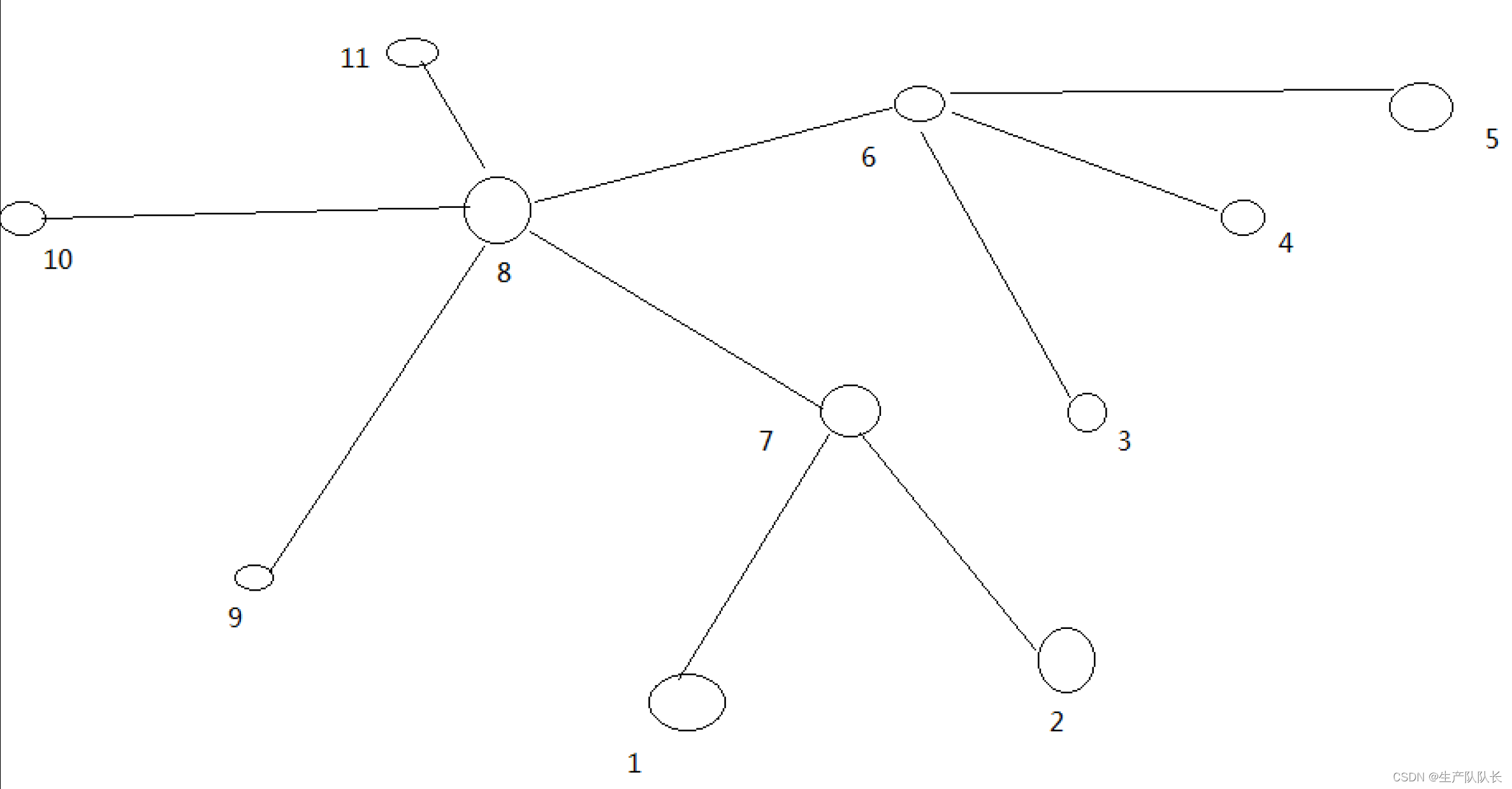
树的结构如下:
各个操作如下:
故输出应依次为 22 和 2121。
代码如下:
//线段树与树链剖分的结合
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#define Rint register int
#define mem(a,b) memset(a,(b),sizeof(a))
#define Temp template<typename T>
using namespace std;
typedef long long LL;
Temp inline void read(T &x){
x=0;T w=1,ch=getchar();
while(!isdigit(ch)&&ch!='-')ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
x=x*w;
}
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define len (r-l+1)
const int maxn=200000+10;
int n,m,r,mod;
//见题意
int e,beg[maxn],nex[maxn],to[maxn],w[maxn],wt[maxn];
//链式前向星数组,w[]、wt[]初始点权数组
int a[maxn<<2],laz[maxn<<2];
//线段树数组、lazy操作
int son[maxn],id[maxn],fa[maxn],cnt,dep[maxn],siz[maxn],top[maxn];
//son[]重儿子编号,id[]新编号,fa[]父亲节点,cnt dfs_clock/dfs序,dep[]深度,siz[]子树大小,top[]当前链顶端节点
int res=0;
//查询答案
inline void add(int x,int y){//链式前向星加边
to[++e]=y;
nex[e]=beg[x];
beg[x]=e;
}
//-------------------------------------- 以下为线段树
inline void pushdown(int rt,int lenn){
laz[rt<<1]+=laz[rt];
laz[rt<<1|1]+=laz[rt];
a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
a[rt<<1|1]+=laz[rt]*(lenn>>1);
a[rt<<1]%=mod;
a[rt<<1|1]%=mod;
laz[rt]=0;
}
inline void build(int rt,int l,int r){
if(l==r){
a[rt]=wt[l];
if(a[rt]>mod)a[rt]%=mod;
return;
}
build(lson);
build(rson);
a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
}
inline void query(int rt,int l,int r,int L,int R){
if(L<=l&&r<=R){res+=a[rt];res%=mod;return;}
else{
if(laz[rt])pushdown(rt,len);
if(L<=mid)query(lson,L,R);
if(R>mid)query(rson,L,R);
}
}
inline void update(int rt,int l,int r,int L,int R,int k){
if(L<=l&&r<=R){
laz[rt]+=k;
a[rt]+=k*len;
}
else{
if(laz[rt])pushdown(rt,len);
if(L<=mid)update(lson,L,R,k);
if(R>mid)update(rson,L,R,k);
a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
}
}
//---------------------------------以上为线段树
inline int qRange(int x,int y){
int ans=0;
while(top[x]!=top[y]){//当两个点不在同一条链上
if(dep[top[x]]<dep[top[y]])swap(x,y);//把x点改为所在链顶端的深度更深的那个点
res=0;
query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
ans+=res;
ans%=mod;//按题意取模
x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
}
//直到两个点处于一条链上
if(dep[x]>dep[y])swap(x,y);//把x点深度更深的那个点
res=0;
query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
ans+=res;
return ans%mod;
}
inline void updRange(int x,int y,int k){//同上
k%=mod;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
update(1,1,n,id[top[x]],id[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
update(1,1,n,id[x],id[y],k);
}
inline int qSon(int x){
res=0;
query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1
return res;
}
inline void updSon(int x,int k){//同上
update(1,1,n,id[x],id[x]+siz[x]-1,k);
}
inline void dfs1(int x,int f,int deep){//x当前节点,f父亲,deep深度
dep[x]=deep;//标记每个点的深度
fa[x]=f;//标记每个点的父亲
siz[x]=1;//标记每个非叶子节点的子树大小
int maxson=-1;//记录重儿子的儿子数
for(Rint i=beg[x];i;i=nex[i]){
int y=to[i];
if(y==f)continue;//若为父亲则continue
dfs1(y,x,deep+1);//dfs其儿子
siz[x]+=siz[y];//把它的儿子数加到它身上
if(siz[y]>maxson)son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号
}
}
inline void dfs2(int x,int topf){//x当前节点,topf当前链的最顶端的节点
id[x]=++cnt;//标记每个点的新编号
wt[cnt]=w[x];//把每个点的初始值赋到新编号上来
top[x]=topf;//这个点所在链的顶端
if(!son[x])return;//如果没有儿子则返回
dfs2(son[x],topf);//按先处理重儿子,再处理轻儿子的顺序递归处理
for(Rint i=beg[x];i;i=nex[i]){
int y=to[i];
if(y==fa[x]||y==son[x])continue;
dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链
}
}
int main(){
read(n);read(m);read(r);read(mod);
for(Rint i=1;i<=n;i++)read(w[i]);
for(Rint i=1;i<n;i++){
int a,b;
read(a);read(b);
add(a,b);add(b,a);
}
dfs1(r,0,1);
dfs2(r,r);
build(1,1,n);
while(m--){
int k,x,y,z;
read(k);
if(k==1){
read(x);read(y);read(z);
updRange(x,y,z);
}
else if(k==2){
read(x);read(y);
printf("%d\n",qRange(x,y));
}
else if(k==3){
read(x);read(y);
updSon(x,y);
}
else{
read(x);
printf("%d\n",qSon(x));
}
}
}习题
洛谷上的所有习题![]() https://www.luogu.com.cn/problem/list?keyword=&tag=228&page=1
https://www.luogu.com.cn/problem/list?keyword=&tag=228&page=1