引言:本篇博客将详细介绍到数据结构中的又一位大将——二叉树。它也是我们目前学到的第一个非线性的数据结构。并且本章将学到的概念居多,希望大家可以理解并牢记。
更多有关C语言和数据结构知识详解可前往个人主页:计信猫
目录
一,树
1,树的概念
2,树的定义
二,二叉树
1,二叉树的概念
2,特殊的二叉树
Ⅰ ,满二叉树
Ⅱ,完全二叉树
3,二叉树的储存
三,结语
一,树
1,树的概念
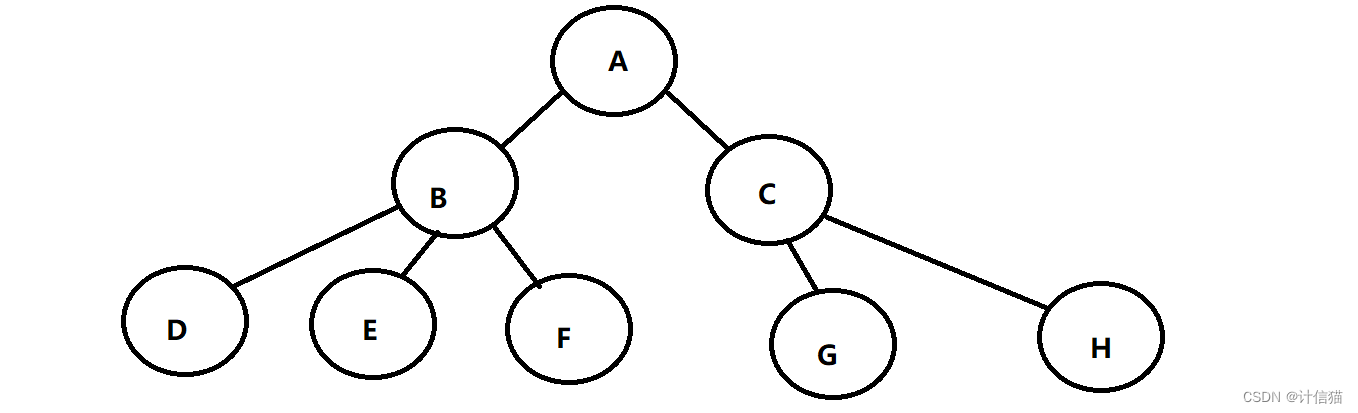
树是一种非线性的数据结构,它由n(n>=0)个有限节点组成一个具有层次关系的集合。而在形式上就像一个倒挂的树,根在上,叶在下。如下图,就是一棵树:
想要真正的了解一棵树,那我们还应该继续掌握关于树的细枝末节的概念知识。
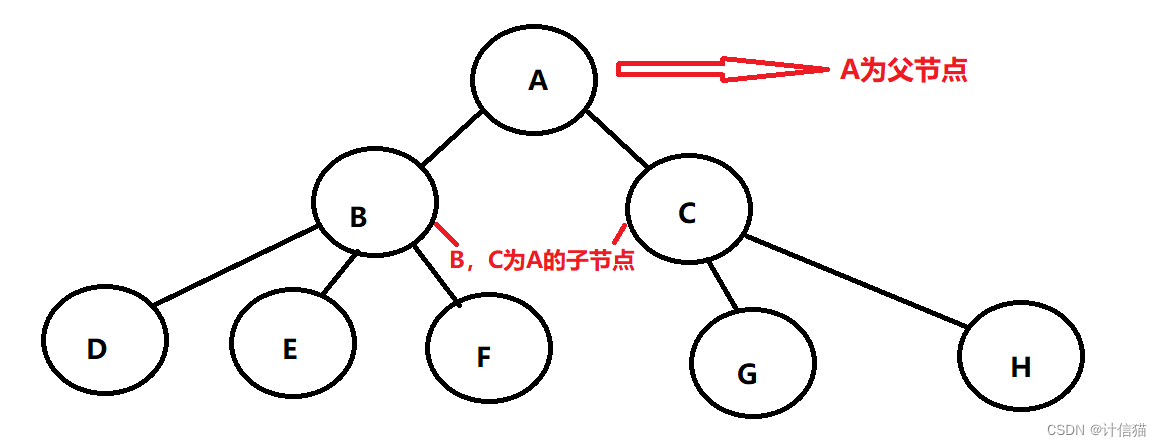
父节点/双亲节点 子节点/孩子节点
节点的度:某节点所含有的子节点的个数。例如A的度就为2
兄弟节点:具有相同父节点的节点。如B,C就为兄弟节点
叶节点/终端节点:无子节点,度为0的节点。如D,E,F,G,H
堂兄弟节点:父节点处于同一层上的节点。
树的度:树所包含的节点中的度的最大值。例如这棵树的度就为3
树的高度:树的最大层次(深度)。例如这棵树的高度就为3
森林:互不相交的树的集合。
当然,我们也会遇到两棵比较特殊的树,如下:
此时空树的度和高度就为0,只有根节点的树的度和高度就为1。
想要成为一棵树,也需要同时遵守以下规则:
1,子树之间便可以有相连或者相交的情况出现。
2,除了根节点以外,每一个节点有且仅有一个父节点。
2,树的定义
对于树的定义,则存在一个难点,那就是一个节点的子节点的个数不确定性,导致我们不知道该定义多少个指针变量合适。
但是,我们可以使用一个方法,叫做左孩子右兄弟定义法来完美地解决这个问题。于是我们如下代码定义一个树:
struct TreeNode
{
int val;
struct TreeNode* LeftChild;//左孩子
struct TreeNode* RightBrother;//右兄弟
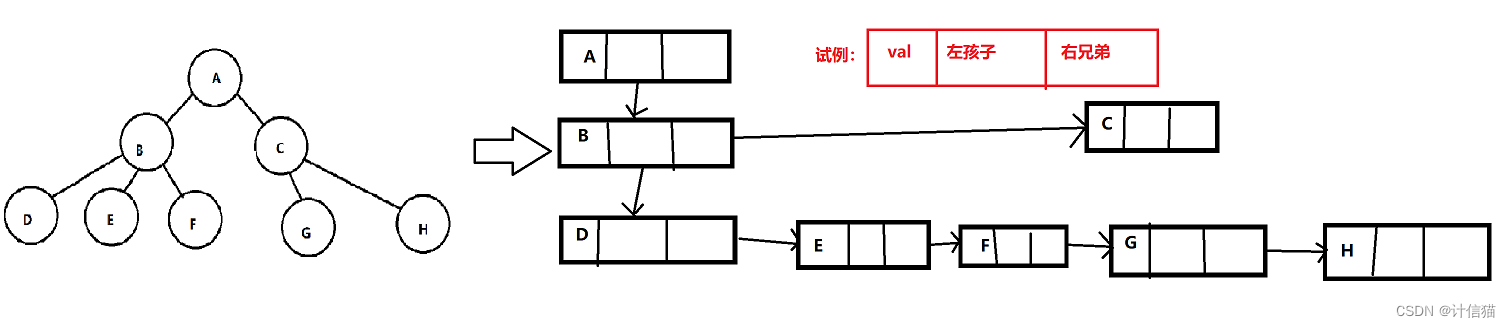
};所以有了这个方法,我们就可以很轻松地将如下的树使用代码进行表示了。
而在使用此方法时,我们必须确保左孩子一定是每一层最左边的那一个。于是我们便可以使用如下代码来遍历一棵树的某一层。
struct TreeNode*cur=parent->LeftChild;//parent表示根节点
while(cur)
{
//……
cur=cur->RightBrother;
}二,二叉树
1,二叉树的概念
二叉树无非本质上就首先是一棵树,所以它拥有树的全部概念。其次二叉树的特殊之处就是二叉树的度为2,也就是说一个节点的子节点数不可以超过2。
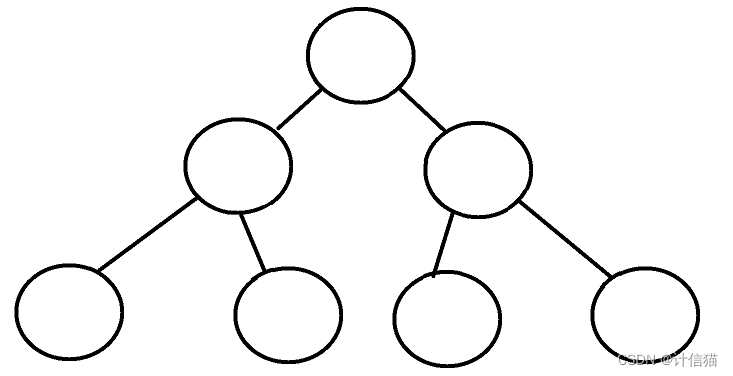
那么如下,就是一棵二叉树:

2,特殊的二叉树
Ⅰ ,满二叉树
满二叉树的定义就是除了叶节点之外,每一个节点都达到含有了两个子节点的二叉树。如下图所示:
倘若满二叉树的高度为H,那么我们便可以计算出它的节点个数:
Ⅱ,完全二叉树
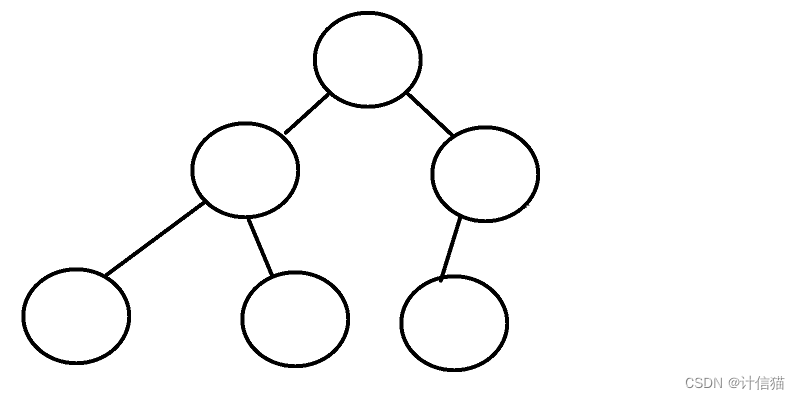
完全二叉树则要求,前H-1层为满二叉树,最后一层的叶节点从左向右连续。如下图所示:
而所要求的”连续“的意思其实就是从左到右必须叶节点紧挨着叶节点,不可以有空出来的位置。
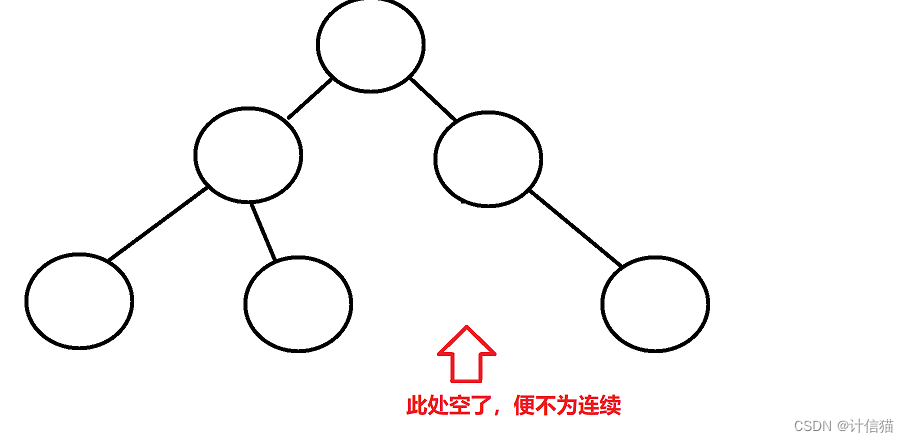
那我们举出如下反例,便不是完全二叉树:
3,二叉树的储存
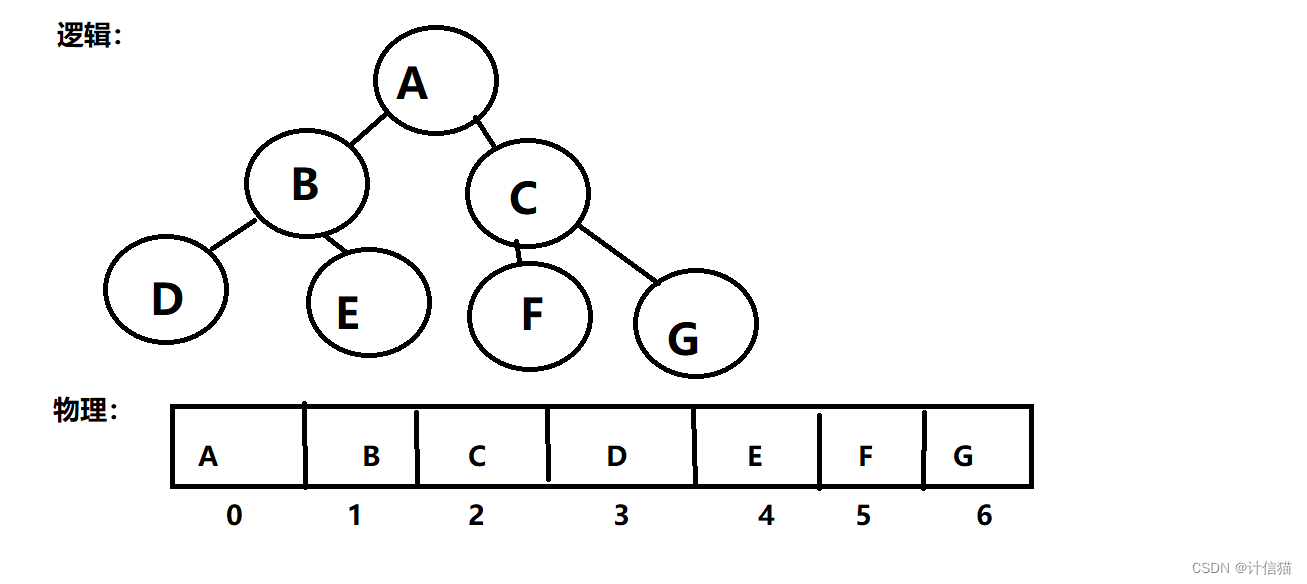
对于二叉树的储存,我们便是将逻辑结构与物理结构进行分离储存。
逻辑结构:树状结构
物理结构:数组结构
利用数组储存二叉树数据的好处就是我们可以使用下标找到某个节点的父节点或者子节点。
通过下标寻找父/子节点
假设父节点的下标为i:左孩子节点的下标为2*i+1,右孩子节点下标为2*i+2。
假设子节点的下标为j:不管j为奇数或者偶数,其父节点的下标都为(j-2)/2——因为会涉及到int类型取整操作。
注意:若为非完全二叉树,则不存在的节点一定要在数组中空出来,不然会导致使用下标寻找父子节点的方法失效。
三,结语
这一篇文章也仅仅只是讲到了二叉树的概念而已,接下来我会尽快更新出二叉树数据结构的应用——堆。
而堆相较于我们以前学到的数据结构就更加的复杂难懂了,如果想要看懂堆,那么将这篇博客所讲到的知识点,尤其是父子节点下标的寻找烂熟于心就是非常重要的了。希望我们可以一起克服我们所遇到的困难,一起加油!