题目：
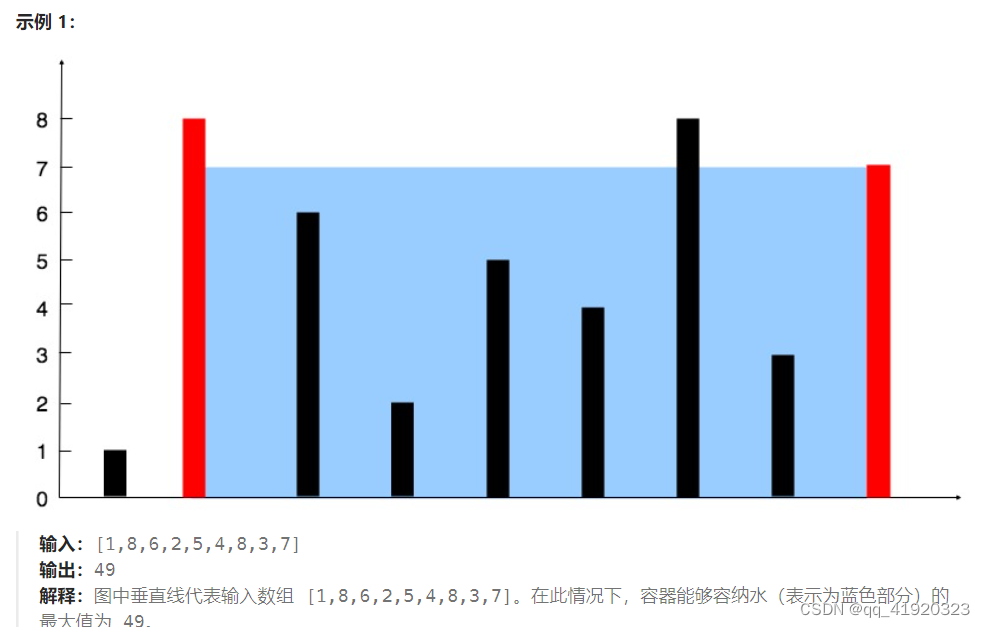
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

C++：双指针解法
要点：指针每一次移动，都意味着排除掉了一个柱子，每次移动有可能会增大面积的那条边。
详细解释请参照：

https://leetcode.cn/problems/container-with-most-water/solutions/94102/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/?envType=study-plan-v2&envId=top-100-liked

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;


class Solution{
public:
	int maxArea(vector<int>& height) {
		//l是左端，r端开始，tmp每次计算出的容积，maxarea每次计算后的最大容积 
		int l = 0, r = height.size() - 1, tmp= 0, maxarea= 0;
		while (l < r){
			tmp= (r - l) *  min(height[l], height[r]);
			//一格指针移动后，取这次计算的area和上次计算的容积哪个大 
			maxarea= max(tmp, maxarea);
			if (height[l] < height[r]){
				l++;
			}
			else{
				r--;
			}
		}
		return maxarea;
	}
};

int main(){
	Solution solution;
	int res;
	vector<int > arr = { 1, 8, 6, 2, 5, 4, 8, 3, 7 };
	res = solution.maxArea(arr);
	cout << res << endl;
	return 0;
}

python：双指针
思路同上；

# 双指针思路：左右两边标记i, j, 两边往中间移(左右夹逼)
class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        maxArea = 0
        l = 0
        r = len(height) - 1
        while l < r:
            minHeight = 0
            if height[l] < height[r]:
                minHeight = height[l]
                l = l + 1
            else:
                minHeight = height[r]
                r = r - 1
            area = (r - l + 1) * minHeight
            maxArea = max(maxArea, area)
        return maxArea