三维空间刚体运动
欧拉角
欧拉角可以说是零理解成本的表示形式,由于有万向锁的问题被绝大部分项目所抛弃。欧拉角的每个轴旋转都有固定好的名称,这些名称十分直观:
- Z轴旋转,相当于左右旋转,叫航角,或偏航角。
- Y轴旋转,相当于俯仰旋转,叫仰角,或俯仰角。
- X轴旋转,相当于一个人躺在地上翻滚,叫滚角,或滚转角。
然而在某些情况下,我们获得到欧拉角,还是需要将其转换为旋转矩阵。14讲中提到了Rodrigues公式,在opencv里有直接实现好的接口。尽量使用这些现成的接口,可以避免很多不必要的麻烦:
R = cv2.Rodrigues(rpy)
rpy = cv2.Rodrigues(R)
cv::Rodrigues(rpy, R);
cv::Rodrigues(R, rpy);
使用欧拉角还需要注意的一个问题是弧度单位制和角度单位制的区别。如果发现单位制需要转换,就需要/180*Pi或者*Pi/180来进行转换。
四元数
四元数在所以到的旋转表示中是最麻烦的,它既不直观,计算也不简便,但是在数学上有着十分优美的表达形式。由于四元数仅使用四个分量就可以无奇异的表示旋转,因此这种表示方式会在传输过程中使用到。一个典型的例子就是ROS消息geometry_msgs/Pose:
orientation.x
orientation.y
orientation.z
orientation.w
position.x
position.y
position.z
采用四元数就可以实现7个数传输一次位姿,用Rt矩阵一共是12个数,T占用16个。但其实这样的数据传输量对总体的系统来说压力并不高,相比图像实时传输的数据量来说是九牛一毛。因此一般不会以传输压力作为选择四元数作为旋转表达的主要原因。在一些工作中,比如VINS,和一些ceres进行优化的标定项目,会主要采用四元数进行最小二乘法的计算。
为了直观的让读者了解四元数,我们模仿前一章的做法,再次把轴旋转的四元数形式列在这里,方便大家理解:
RPY Quaternion
0, 0, 0 [ 0, 0, 0, 1 ]
90,0,0 [
2
2
\frac{\sqrt{2}}{2}
22, 0, 0,
2
2
\frac{\sqrt{2}}{2}
22]
0,90,0 [ 0,
2
2
\frac{\sqrt{2}}{2}
22, 0,
2
2
\frac{\sqrt{2}}{2}
22]
0,0,90 [ 0, 0,
2
2
\frac{\sqrt{2}}{2}
22,
2
2
\frac{\sqrt{2}}{2}
22]
旋转x轴90度,如果进行手算的话,可能会得到类似[1 0 0 1]的结果,这个结果的膜长是大于1的,需要进行规范化之后才会变成标准表达形式。因此最终是[
2
2
\frac{\sqrt{2}}{2}
22, 0, 0,
2
2
\frac{\sqrt{2}}{2}
22]。
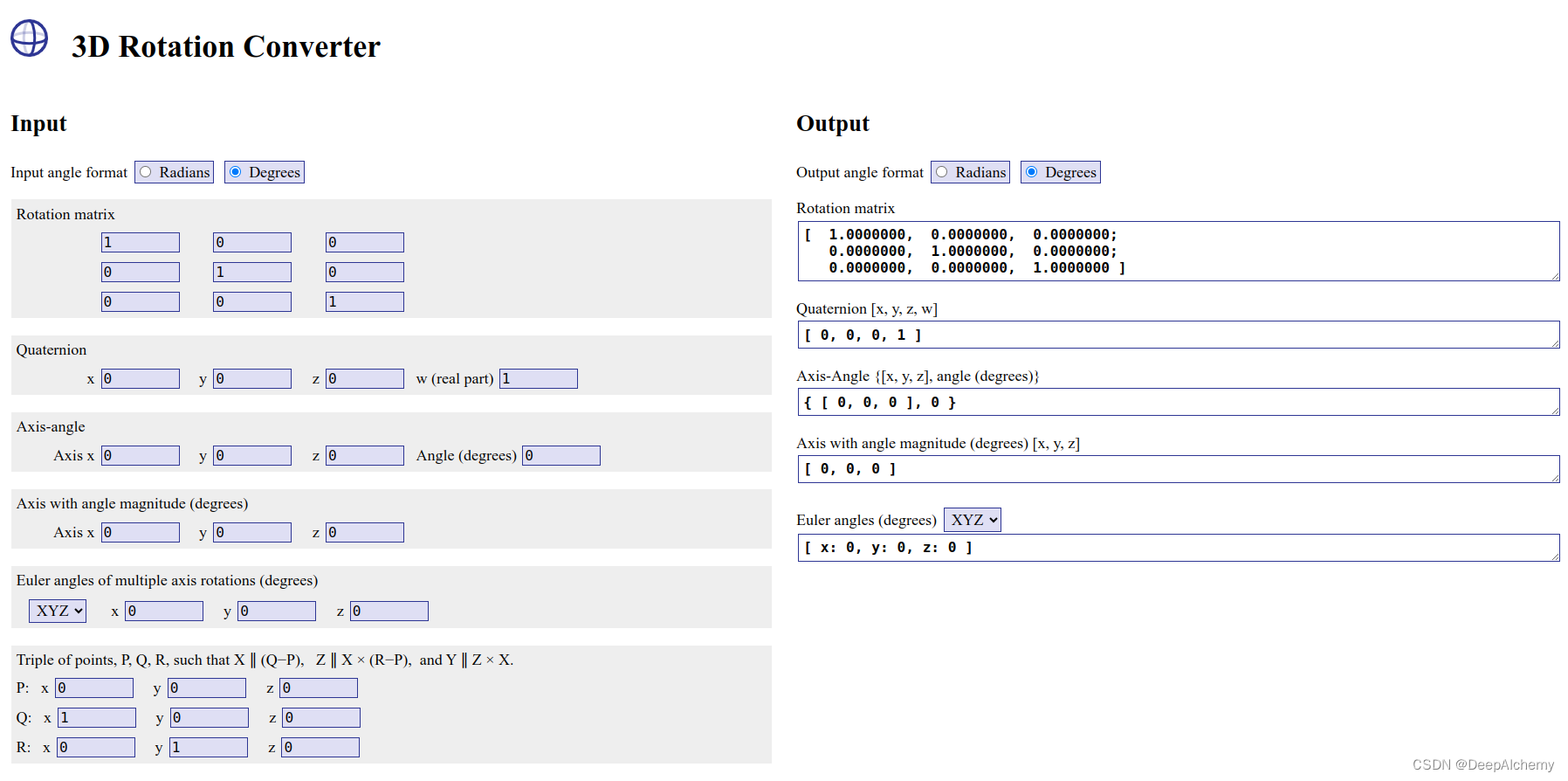
小工具
最后推荐一个网站,3D Rotation Converter作为一个在线旋转形式转化的小工具,可以帮助我们将任一旋转转化成14讲中提到的人以一种形式。