目录
什么是数据结构
数据与结构
什么是算法
复杂度分析
时间复杂度与空间复杂度
时间复杂度
思考:
空间复杂度
常数阶O(1)
对数阶O(logn)
线性阶O(n)
以下为空间复杂度为O(n)
线性对数阶O(nlogn)
平方阶O(n)
指数阶O(2^n)
什么是数据结构
数据结构是由:“数据”与“结构”两部分组成
数据与结构
数据:如我们所看见的广告、图片、视频等,常见的数值,教务系统里的(姓名、性别、学号、学历等等);
结构:当我们面对海量的数据时,我们时常无法下手,寻找数据是不方便的,可读性就很差;而结构则是将这些数据以各种不同的形式进行排序,使我们便于寻找;
数据结构:是计算机存储、组织数据的方式。是数据之间存在一种或多种相互关系的集合;

什么是算法
算法(Algorithm)就是定义良好的计算过程,他取出一个或一组数据为输入,产出一个或一组的值为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
算法一般分为:排序,递归与分治,回溯,DP,贪心,搜索算法、二分查找、水桶法等等;
- 算法往往数学密切相关,就如数学题一样,每道数学题都有不同的解法,算法也是同理
复杂度分析
我们如何评判算法的效率呢,问题的解决方法有很多,对于计算机而言,我们需要找到问题的最优解,为了寻找到这个最优解,我们需要从两个维度评判
- 时间效率:算法运行的快慢
- 空间效率:算法所占空间的大小
评估方法:实验分析与理论分析
对于实验分析而言:
- 相同的算法在不同的电脑,它们所运行的时间也许会有很大的出入;
- 当面对大量的数据而言,同一台电脑时间上的差距则会变为很大,导致误差的增大;
- 有些算法在少量数据时运算速度不快,在大量数据中反之;
由于实验分析法的局限性,就有人提出了一种理论测评的方法,就是渐近复杂度分析(asymptotic complexity analysis),简称复杂度分析。
这种方法体现算法运行所需的时间(空间)资源与输入数据大小之间的关系,能有效的反应算法的优劣。
时间复杂度与空间复杂度
时间复杂度
指一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。让我们计算下方代码的时间复杂度
int main()
{
int n=10;//对于时间复杂度而言,当数据为n时,下方代码区,运行次数10,时间复杂度为O(n)
while (n--) {
printf("%d", n);
}//在时间复杂度中,我们会忽略除最高次的所有项
//忽略所有系数
return 0;
}实际上我们不可能对执行次数的统计精确,并且为理论分析,当n->∞时,最高次的影响会远远超过非最高次的项,所以O(n)的数量级由最高次决定,所以当我们计算时间复杂度时,可以简化为以下两个步骤
- 忽略除最高次的所有项
- 忽略所有系数
思考:
当我们遍历下方数组,查找2时,我们需要4次;

当长度为n的数组中存放的是无序自然数时,他们是没有规则的,此时我们查找2的次数:[ 1 , n ]
此时我们需要将最坏的情况作为时间复杂度
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度的表示也遵循大O的渐进表示法
让我们计算一下冒泡排序的空间复杂度
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}//在冒泡排序中,我们只开辟了一块空间,所以空间复杂度为O(1);复杂度的分类
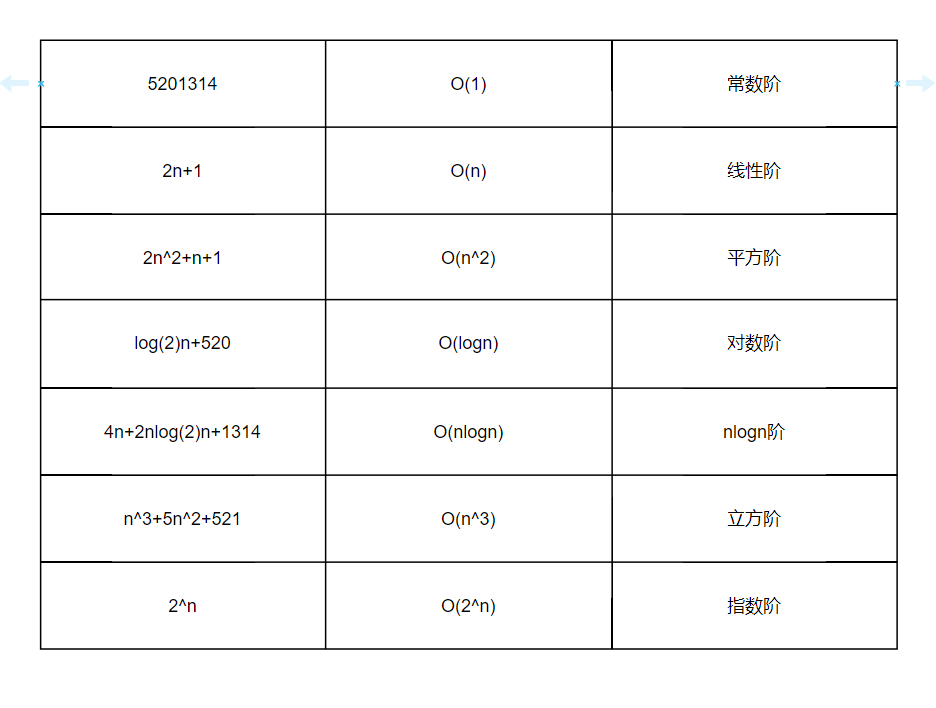
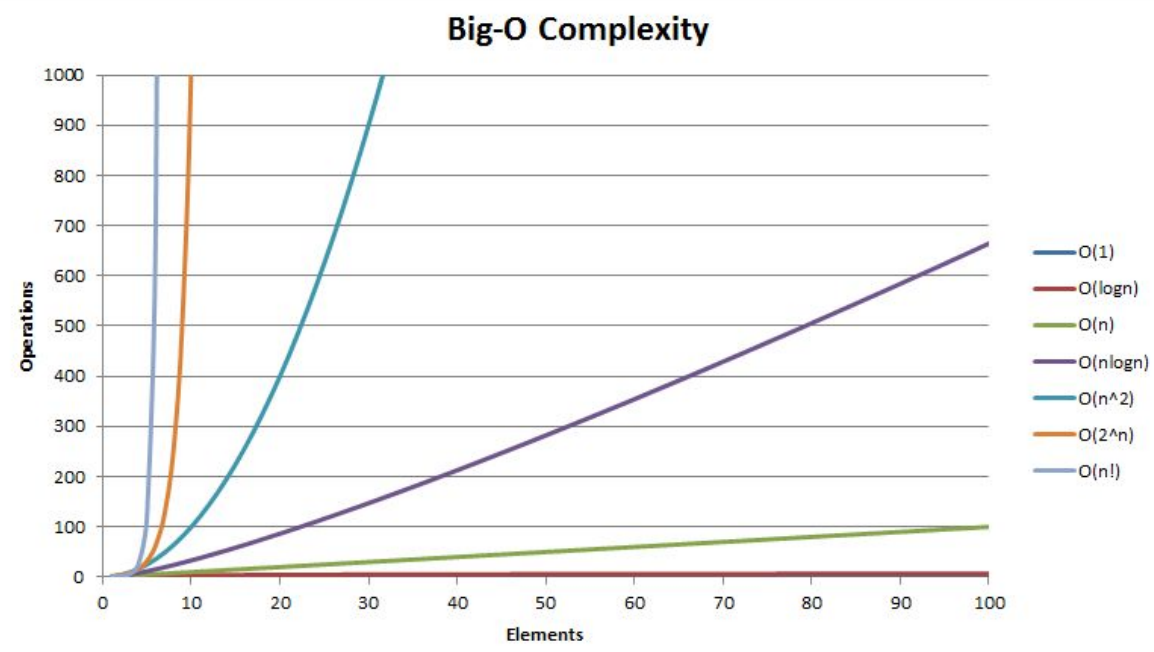
算法的复杂度有几个量级,表示如下:
O(1)<O(logN)<O(N)<O(NlogN)<O(N2)<O(2N)<O(N!)
如图下列:
常数阶O(1)
int main()
{
int n = 4;
while (n--) {
printf("%d", n);//执行次数为常数
}
return 0;
}对数阶O(logn)
int binary_search(int nums[], int size, int target)
//nums是数组,size是数组的大小,target是需要查找的值
{ int left = 0;
int right = size - 1;
// 定义了target在左闭右闭的区间内,[left, right]
while (left <= right) {
//当left == right时,区间[left, right]仍然有效
int middle = left + ((right - left)>>1);//等同于 (left + right) / 2,防止溢出
if (nums[middle] > target) {
right = middle - 1; //target在左区间,所以[left, middle - 1]
}
else if (nums[middle] < target) {
left = middle + 1; //target在右区间,所以[middle + 1, right]
}
else { //既不在左边,也不在右边,那就是找到答案了
return middle;
}
}
//没有找到目标值
return -1;
}
线性阶O(n)
int main()
{
int n;
scanf("%d", &n);
int court = 0;
for (int i = 0; i < n; i++) {
court += i;//计算和
}
return 0;
}以下为空间复杂度为O(n)
int main()
{
int n;
scanf("%d", &n);
int* p = (int*)malloc(sizeof(int) * n);
//开辟大小为n的空间
if (p == NULL)
{
perror("malloc fail");
return -1;
}
free(p);
p = NULL;
}线性对数阶O(nlogn)
无论是时间复杂度还是空间复杂度,线性对数阶都是在循环嵌套里实现,即为一层为O(n),另一层为O(logn);
所以我们可以利用二分查找+打印
int binary_search(int nums[], int size, int target) //nums是数组,size是数组的大小,target是需要查找的值
{
int left = 0;
int right = size - 1; // 定义了target在左闭右闭的区间内,[left, right]
while (left <= right) { //当left == right时,区间[left, right]仍然有效
int middle = left + ((right - left) / 2);//等同于 (left + right) / 2,防止溢出
if (nums[middle] > target) {
right = middle - 1; //target在左区间,所以[left, middle - 1]
}
else if (nums[middle] < target) {
left = middle + 1; //target在右区间,所以[middle + 1, right]
}
else { //既不在左边,也不在右边,那就是找到答案了
printf("%d ", nums[middle]);
}
}
//没有找到目标值
return -1;
}
void func(int nums[], int size, int target)
{
for (int i = 0; i < size; i++)
{
binary_search(nums, size, target);
}
}平方阶O(n)
莫过于我们最为熟悉的冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}指数阶O(2^n)
指数阶的算法效率低下,并不常见
最为常见的指数阶为递归实现斐波那契数列
int Fib1(int n)
{
if (n == 1 || n == 2)
{
return 1;
}
else
{
return Fib1(n - 1) + Fib1(n - 2);
}
}