前面我们已经学习了一些排队模型，对排队系统有了基本认知，本期小编带大家继续来学习其他排队模型的内容。

 一、有限源排队模型

顾客源为有限的这类排队问题的主要特征是顾客总数是有限的，如只有m个顾客。每个顾客来到系统中接受服务后仍回到原来的总体，还有可能再来，这类排队问题的典型例子是机器看管问题。如一个工人同时看管m台机器，当机器发生故障时即停下来等待修理，修好后再投入使用，且仍然可能再发生故障。

有限排队模型与M/M/1/∞/∞的区别？

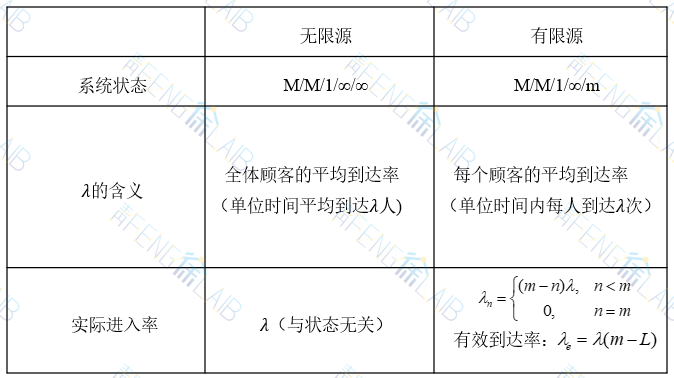
    关于顾客的平均到达率，在无限源的情形中是按全体顾客来考虑的，而在有限源的情形下，必须按每一顾客来考虑。设每个顾客的到达率都是相同的，均为λ(这里λ的含义是指单位时间内该顾客来到系统请求服务的次数)，且每一顾客在系统外的时间均服从参数为λ的负指数分布。由于在系统外的顾客的平均数为m-L，故系统的有效到达率为

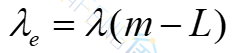
平稳状态下，队长N的分布为：

状态间的转移概率为：

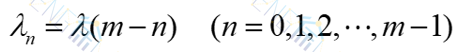
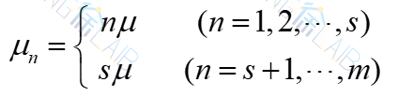
01多服务台（s） 

多服务台(s)的情况下，系统生灭过程如下：

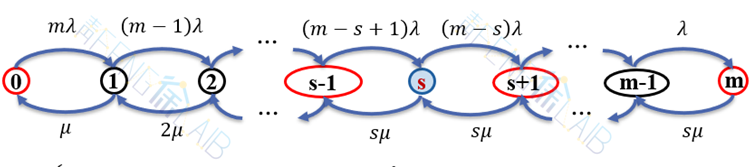
由生灭过程可得到状态平衡方程：

 

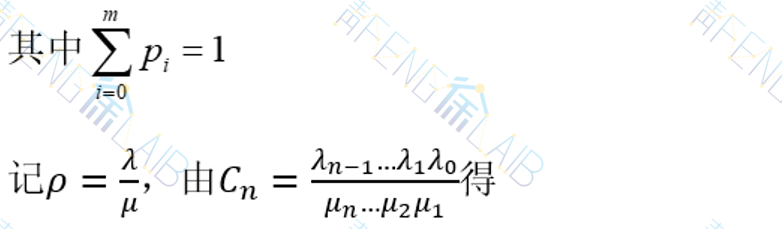
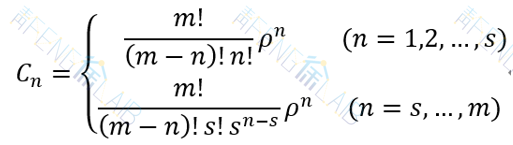
由

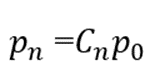
得

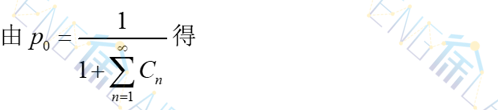
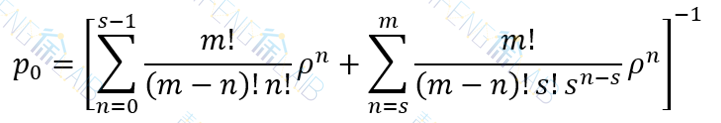
 下面给出系统的有关运行指标：

平均排队长

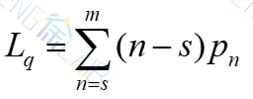
平均队长

 

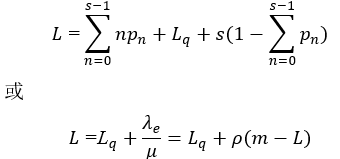
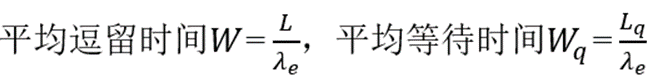
02 单服务台（s=1）

特别是对单服务台（s=1）系统，有：

若系统的相对通过能力Q=1，绝对通过能力为

 

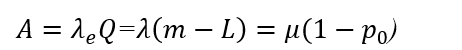
03 案例

设有一工人看管5台机器，每台机器正常运转的时间服从负指数分布，平均为15min。当发生故障后，每次修理时间服从负指数分布，平均为12min，试求该系统的有关运行指标。

解：用有限源排队模型处理本问题。

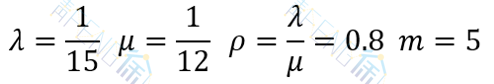
(1) 修理工人空闲的概率

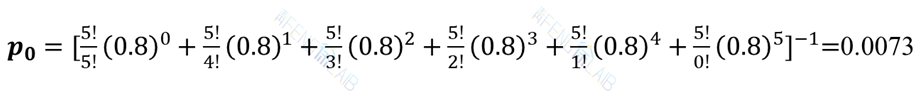
(2) 5台机器都出故障的概率

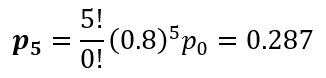
(3) 出故障机器的平均数

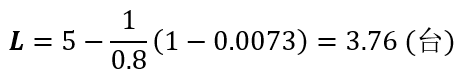
(4) 等待修理机器的平均数

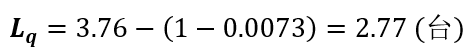
(5) 每台机器发生一次故障的平均停工时间

(6) 每台机器平均待修时间

(7) 系统绝对通过能力（即工人的维修能力）

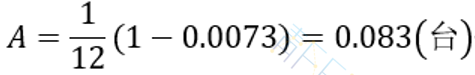
即该工人每小时可修理机器的平均台数为

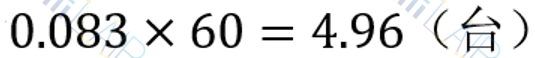
上述结果表明，机器停工时间过长，看管工人几乎没有空闲时间，应采取措施提高服务率或增加工人。

二、服务率或到达率依赖状态的排队模型

实际排队问题中，到达率或服务率可能是随系统状态而变化的。对单服务台系统而言，实际到达率和服务率均依赖于所处的状态n，可假设为

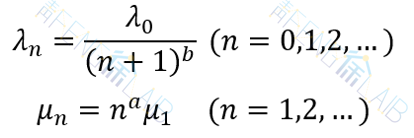
对多服务台系统而言，实际到达率和服务率假设为

其中，λn和μn分别为系统处于状态n时的到达率和服务率。上述假设表明：到达率λn与系统中已有顾客数n呈反比，服务率μn与系统状态n呈正比。

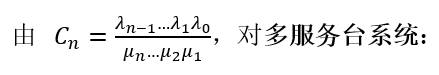
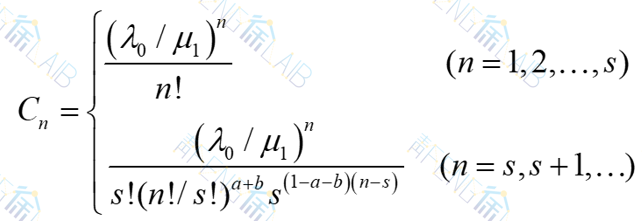
下面来看一个简单的特例，考虑一个到达依赖状态的单服务台等待制系统M/M/1/∞，其参数为

 三、非生灭过程排队模型

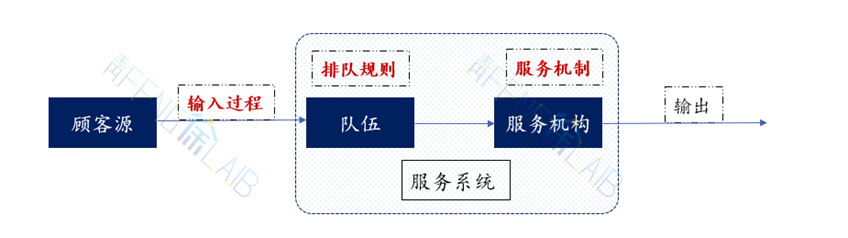
一个排队系统的特征是由输入过程，服务机制和排队规则决定的，上图为生灭过程排队模型，特点如下：

输入过程：顾客相继到达时间间隔的分布为Poisson分布；

服务机制：服务时间服从负指数分布。

这类排队系统的一个主要特征是马尔可夫性，而马尔可夫性的一个主要性质是由系统当前的状态可以推断未来的状态。

但是，当输入过程不是Poisson流或服务时间不服从负指数分布时，仅知道系统内当前的顾客数，对于推断系统未来的状态是不充足的，因为正在接受服务的顾客，已经被服务了多长时间，将影响其离开系统的时间。因此，必须引入新的方法来分析具有非负指数分布的排队系统。

对一般具有非负指数分布的排队系统的分析是非常困难的，需要较多的数学知识。下面仅就几种特殊情形给出有关的结果。

01 M/G/1排队模型

顾客到达为Poisson流，单个服务台，服务时间为一般分布的排队系统。现假设顾客平均到达率为λ，服务时间均值为1/μ，方差为，则可证明：当

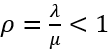
时，系统可以达到平稳状态。

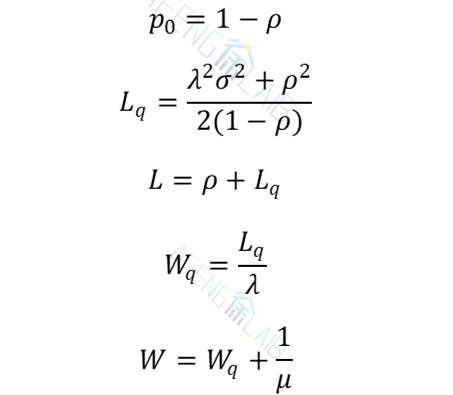
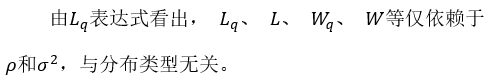
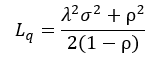
02 案例

有一汽车冲洗台，汽车按Poisson流到达，平均每小时到达18辆，冲洗时间V，根据过去的经验表明，有E(V)=0.05h/辆，Var(V)=0.01(h/辆)2 ，求相关运行指标，并对系统进行评价。

解：本例中

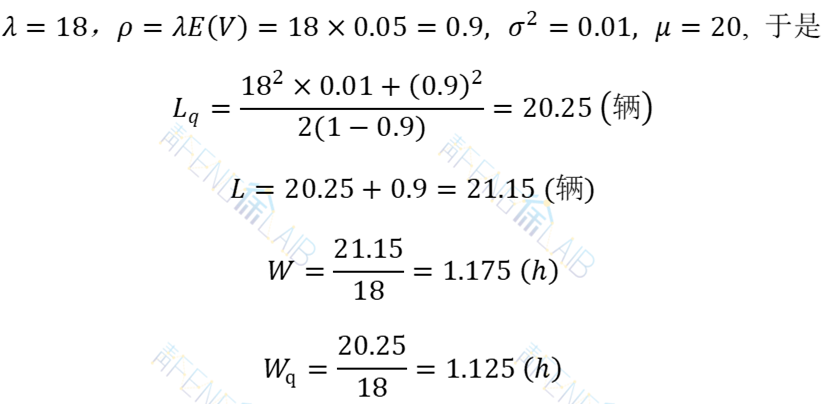
这个服务机构很难令顾客满意，突出问题是顾客的平均等待时间是服务时间的

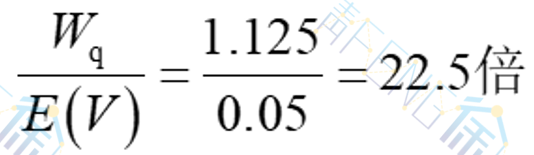
即顾客的时间损失系数。

03 爱尔朗（Erlang）排队模型

爱尔朗分布族比负指数分布族对现实世界具有更广泛的适应性。由于服务时间为k阶Erlang分布，其分布密度函数为

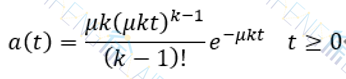
故其均值和方差分别为

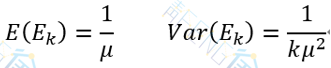
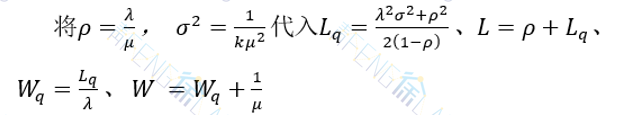
得到

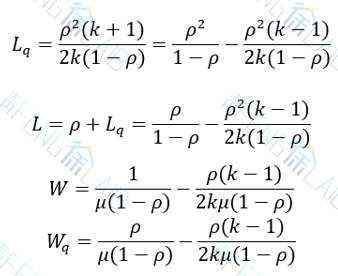
以上就是关于其他排队模型简介的全部内容了，学习完这一节，大家可以试着对一些实际问题进行应用练习。下一次小编将带大家学习排队系统的优化，敬请关注！

作者 | 陈梦 杨悦

责编 | 王一静

审核 | 徐小峰