LeetCode题练习与总结：不同的二叉搜索树--96

news2024/10/5 21:14:16

一、题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

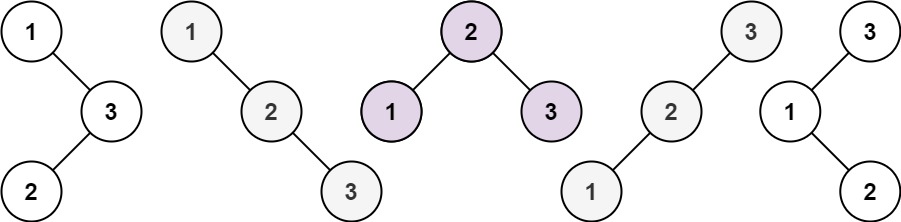
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 19

二、解题思路

这个问题是关于卡特兰数的经典问题。二叉搜索树（BST）的一个重要特性是，它的中序遍历结果是一个有序数组。因此，如果我们有 n 个互不相同的节点，那么可能的二叉搜索树的种数与这些节点的排列方式有关。

对于给定的 n，我们可以这样考虑：

选择 1 作为根节点，那么剩下的 n-1 个节点将位于根节点的右侧，可以形成 G(n-1) 种 BST。
选择 2 作为根节点，那么剩下的 n-2 个节点中，1 个位于根节点的左侧，n-3 个位于根节点的右侧，可以形成 G(1) * G(n-3) 种 BST。
以此类推，直到选择 n 作为根节点，剩下的 n-1 个节点将位于根节点的左侧，可以形成 G(n-1) 种 BST。

因此，G(n) 可以用以下公式表示：G(n)=G(0)∗G(n−1)+G(1)∗G(n−2)+...+G(n−1)∗G(0)

其中 G(0) = 1，因为只有一个节点的 BST 只有一种情况。

基于上述思路，我们可以用动态规划的方法来解决这个问题。我们可以创建一个数组 dp，其中 dp[i] 表示有 i 个节点时可能的 BST 种数。然后我们可以按照上述公式计算 dp 数组。

三、具体代码

public class Solution {
    public int numTrees(int n) {
        if (n == 0) return 1;
        
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        
        return dp[n];
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

我们有一个双重循环结构。外层循环遍历从 2 到 n 的所有整数，共执行 n - 1 次。
内层循环遍历从 1 到当前外层循环的整数，最坏情况下（即外层循环变量为 n 时）执行 n 次。
因此，内层循环总共执行次数为 1 + 2 + … + n，这是一个等差数列求和，其和为 (n * (n + 1)) / 2。
所以，总的时间复杂度为 O((n * (n + 1)) / 2)，简化后为 O(n^2)。

2. 空间复杂度

我们使用了一个大小为 n+1 的数组 dp 来存储中间结果。
因此，空间复杂度是 O(n)，即与输入大小 n 成正比。

综上所述，代码的时间复杂度是 O(n^2)，空间复杂度是 O(n)。

五、总结知识点

动态规划（Dynamic Programming, DP）：这是一种用于解决优化问题的算法思想，它将复杂问题分解为多个子问题，通过解决子问题来构建原问题的解。动态规划通常用于解决具有重叠子问题和最优子结构特性的问题。
二叉搜索树（Binary Search Tree, BST）：这是一种特殊的二叉树，其中每个节点都满足左子树中的所有元素小于该节点的值，右子树中的所有元素大于该节点的值。题目要求计算不同结构的BST的数量。
卡特兰数（Catalan number）：这是一个组合数学中的数列，用于计算不同结构的二叉树的数量。第 n 个卡特兰数可以通过公式 C(n) = (2n)! / ((n+1)! * n!) 计算得出，其中 n! 表示 n 的阶乘。
循环结构：代码中使用了两个嵌套的 for 循环，这是一种常见的控制结构，用于重复执行代码块固定的次数。
数组的使用：代码中使用了一个整数数组 dp 来存储中间结果，这是一种常见的数据结构，用于存储多个相同类型的数据项。
累加操作：在动态规划的过程中，通过累加操作计算 dp 数组的值，这是动态规划中更新状态的一种常见方式。
边界条件处理：代码中对于 n=0 和 n=1 的情况进行了特殊处理，这是因为在这些情况下，BST 的数量是确定的，分别为 1。