【数据结构】红黑树（定义性质、插入、查找、删除）解析+完整代码

news2024/11/16 23:44:09

3.3 红黑树

3.3.1 定义和性质

  • 为什么发明红黑树？

    平衡二叉树和红黑树的时间复杂度相同，但是平衡二叉树的平衡特性容易被破坏，需要频繁调整树的形态。

    红黑树RBT：插入/删除很多时候不会破坏红黑特性，无需频繁调整树的形态，即需要调整，也可在常数级时间内完成。

    • 平衡二叉树：适用于以查为主，少插入删除的场景；

      红黑树，适用于频繁插入、删除的场景，实用性更强。

  • 定义

    • 红黑树是二叉排序树 ==》左子树结点<=根结点<= 右子树结点

    • 与普通BST相比，有什么要求？ ==》

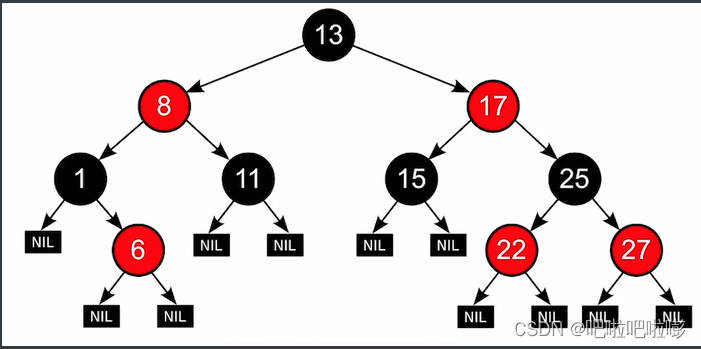
      1.每个结点不是红色就是黑色；

      2.根结点是黑色；

      3.叶结点（外部结点、NULL结点、失败结点）均是黑色；

      4.不存在连续两个红色结点（父子不能同为红色）；

      5.对每个结点，从该结点到任一叶结点的简单路径上，所含黑结点的数目相同。

    • 黑高

      结点的黑高bh——从某结点出发（不含该结点），到达任一空叶结点的路径上黑结点总数。

  • 性质

    1.从根结点到叶结点的最长路径不大于最短路径的2倍；

    证明：任何一条查找失败路径上黑结点数都相同，而路径上不能连续出现两个红结点，即红结点只能穿插在各个黑结点中间。

    ​ 则最长路径为红结点穿插在黑结点间，最短路径是没有红结点。

    2.有n个内部节点的红黑树高度 h < = 2 l o g 2 ( n + 1 ) h<=2log_2(n+1) h<=2log2​(n+1)

    ​ ==》 红黑树查找操作时间复杂度 O ( l o g 2 n ) O(log_2n) O(log2​n)

    证明：若红黑树总高度=h，则根结点黑高>=h/2，因此内部结点数 n > = 2 h / 2 − 1 n>=2^{h/2}-1 n>=2h/2−1，由此推出 h < = 2 l o g 2 ( n + 1 ) h<=2log_2(n+1) h<=2log2​(n+1)

  • 与黑高相关的推论

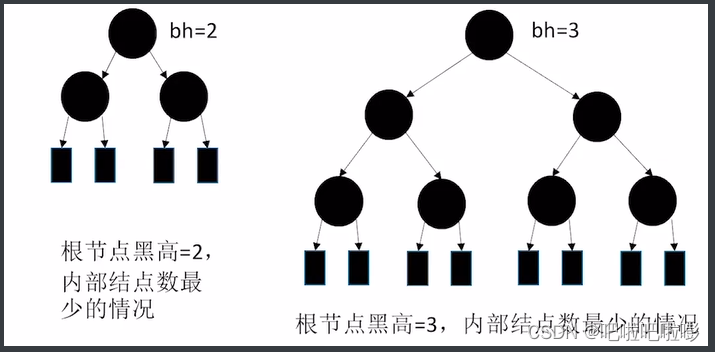
    • 根结点黑高为h的红黑树，内部结点数（关键字）至少有多少个？

      内部结点数最少的情况——总共h层黑结点的满树形态。

      结论：若根结点黑高为h，内部结点数（包含关键字的结点）最少有 2 h − 1 2^h-1 2h−1个

      在这里插入图片描述

3.3.2 查找
  • 与BST、AVL相同，从根出发，左小右大，若查找到一个空叶结点，则查找失败。
3.3.3 插入

  • 方法

    • 先查找，确定插入位置（原理同二叉排序树），插入新结点；

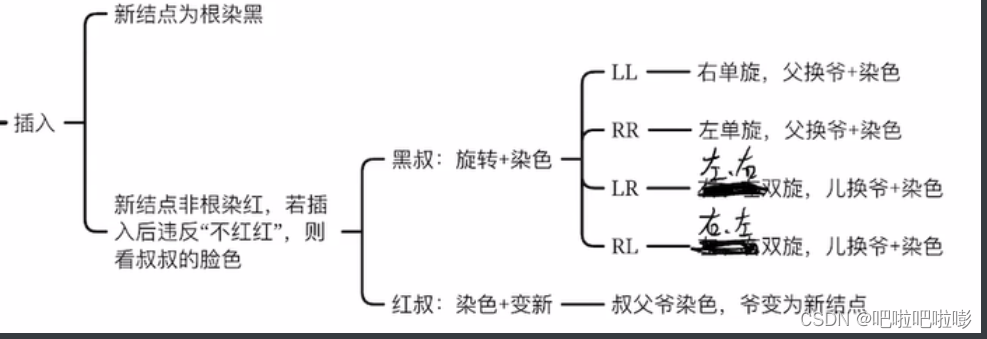
    • 若新结点是根——染黑色；

    • 若新结点非根——染为红色；

      • 若插入新结点后依然满足红黑树定义，则插入结束
      • 若插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义
        • 黑叔：旋转+染色
          • LL型：右单旋，父换爷+染色
          • RR型：左单旋，父换爷+染色
          • LR型：左右双旋，儿换爷+染色
          • RL型：右左双旋，儿换爷+染色
        • 红叔：染色+变新

    在这里插入图片描述

  • 口诀

    左根右——RBT是一种BST，需满足左<根<右

    根叶黑——根结点和叶结点一定是黑色

    不红红——任何一条查找路径上不能连续出现两个红结点

    黑路同——从任一结点出发，达到任一空叶结点的路径上经过的黑结点数量相同

  • 例题

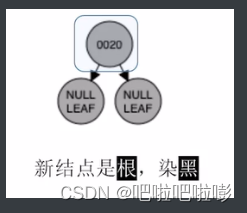
    在这里插入图片描述

    • 插入20

      把20作为根结点插入，并且满足根结点为黑的特性，把该结点染黑。

    在这里插入图片描述

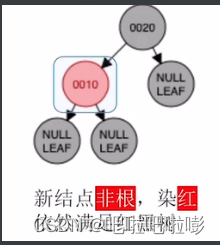
    • 插入10

      因为新结点是非根结点，为了满足任一路径上黑结点数相同，所以染为红色插入。

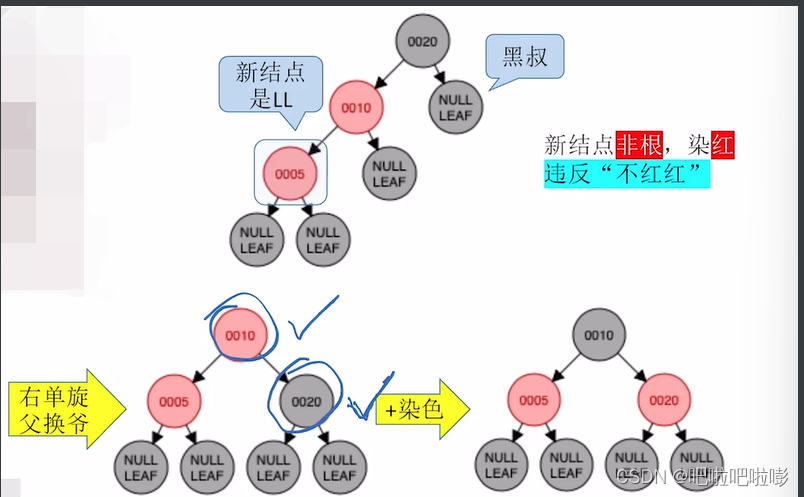
    • 插入5

      新结点是非根结点，染成红色插入，

      但是违反了父子不能同为红的特性，所以要看叔叔结点是什么颜色；

      叔叔结点是黑色（黑叔），则要进行旋转+染色；

      因为新结点是LL型，所以旋转时遵循右单旋，父换爷；

      旋转后，根据红黑树特性染色。

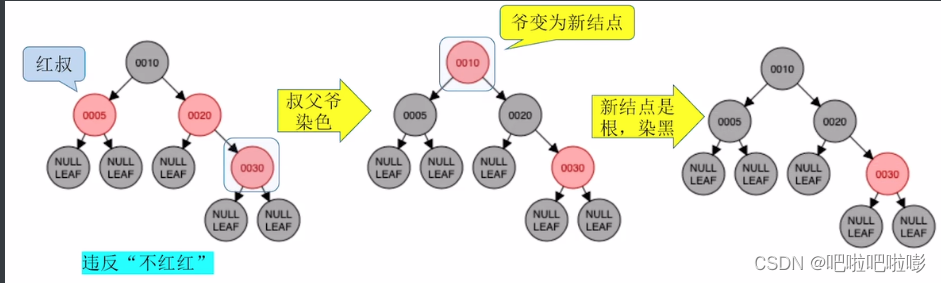
    • 插入30

      新结点插入后违反父子不能同为红的特性，

      叔叔是红色（红叔），则遵循染色+变新，即叔父爷染色（改变颜色），爷变成新结点。

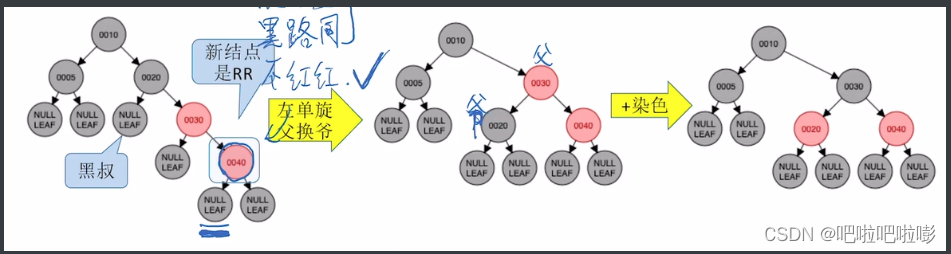
    • 插入40

      插入后违反父子不能同为红的特性；

      叔叔是黑色，新结点是RR型，

      则要左单旋，父换爷+染色

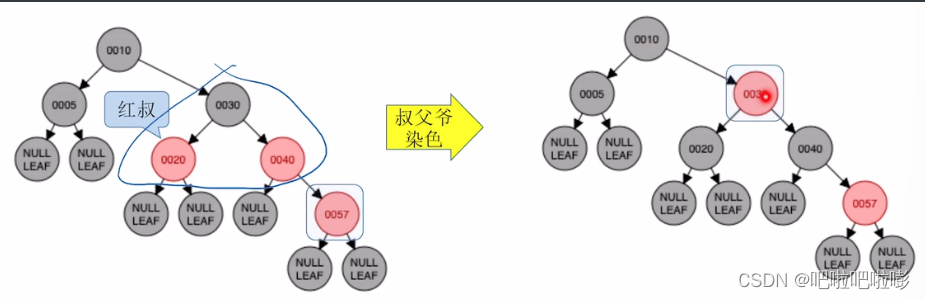
    • 插入57

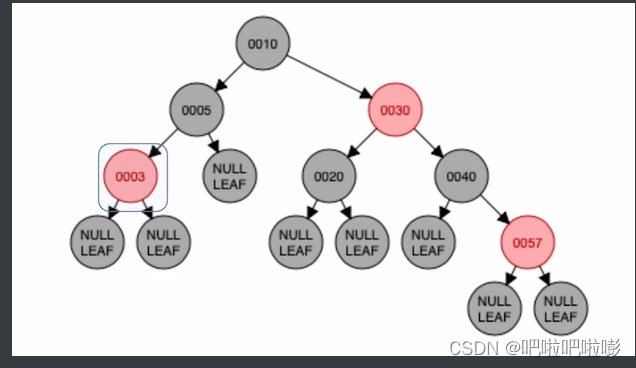
    • 插入3

      不会破坏特性，所以不需要变

    • 插入2

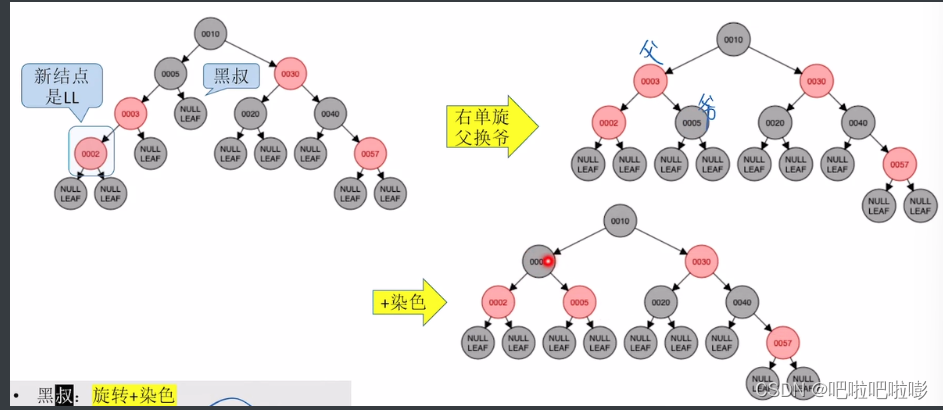
    • 最后结果

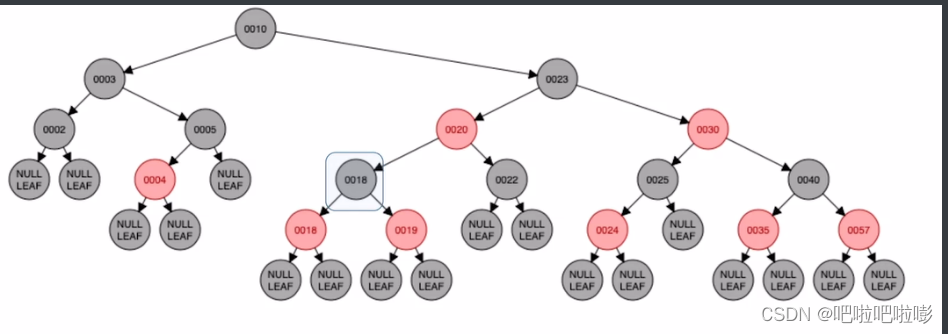
3.3.4 删除

  • 重点

    1.红黑树删除操作的时间复杂度= O ( l o g 2 n ) O(log_2n) O(log2​n)；

    2.在红黑树中删除结点的处理方式和二叉排序树的一样；

    3.按第2步删除结点后，可能破坏红黑树特性，此时需要调整结点颜色、位置，使其再次满足红黑树特性。

*完整代码 红黑树
#include <stdio.h>
#include <stdlib.h>

#define RED 0
#define BLACK 1

// 定义红黑树节点的结构
struct Node {
    int data;           // 节点存储的数据
    int color;          // 节点的颜色，红色为0，黑色为1
    struct Node *left, *right, *parent;    // 左子节点、右子节点、父节点指针
};

typedef struct Node Node;    // 将结构体 Node 重命名为 Node

// 创建一个新节点，并初始化数据
Node* createNode(int data) {
    // 分配内存空间给新节点
    Node* newNode = (Node*)malloc(sizeof(Node));
    // 初始化新节点的数据和颜色（红色）
    newNode->data = data;
    newNode->color = RED;
    // 将左右子节点和父节点指针都设置为 NULL
    newNode->left = newNode->right = newNode->parent = NULL;
    return newNode;
}

// 在给定节点处执行左旋转
void rotateLeft(Node **root, Node *x) {
    // 将 x 的右子节点保存在 y 中
    Node *y = x->right;
    // 将 x 的右子节点设置为 y 的左子节点
    x->right = y->left;
    // 如果 y 的左子节点非空，则更新其父节点指针指向 x
    if (y->left != NULL)
        y->left->parent = x;
    // 将 y 的父节点指针指向 x 的父节点
    y->parent = x->parent;
    // 如果 x 是根节点，则将根节点更新为 y
    if (x->parent == NULL)
        (*root) = y;
        // 如果 x 是其父节点的左子节点，则将 y 设为 x 的父节点的左子节点
    else if (x == x->parent->left)
        x->parent->left = y;
        // 如果 x 是其父节点的右子节点，则将 y 设为 x 的父节点的右子节点
    else
        x->parent->right = y;
    // 将 x 设为 y 的左子节点
    y->left = x;
    // 将 x 的父节点设为 y
    x->parent = y;
}

// 在给定节点处执行右旋转
void rotateRight(Node **root, Node *y) {
    // 将 y 的左子节点保存在 x 中
    Node *x = y->left;
    // 将 y 的左子节点设置为 x 的右子节点
    y->left = x->right;
    // 如果 x 的右子节点非空，则更新其父节点指针指向 y
    if (x->right != NULL)
        x->right->parent = y;
    // 将 x 的父节点指针指向 y 的父节点
    x->parent = y->parent;
    // 如果 y 是根节点，则将根节点更新为 x
    if (y->parent == NULL)
        (*root) = x;
        // 如果 y 是其父节点的左子节点，则将 x 设为 y 的父节点的左子节点
    else if (y == y->parent->left)
        y->parent->left = x;
        // 如果 y 是其父节点的右子节点，则将 x 设为 y 的父节点的右子节点
    else
        y->parent->right = x;
    // 将 y 设为 x 的右子节点
    x->right = y;
    // 将 y 的父节点设为 x
    y->parent = x;
}

// 修正插入操作可能导致的红黑树性质违反
void fixViolation(Node **root, Node *z) {
    // 当插入节点不是根节点且父节点为红色时，需要进行修正
    while (z != *root && z->parent->color == RED) {
        // 当父节点是祖父节点的左子节点时
        if (z->parent == z->parent->parent->left) {
            Node *y = z->parent->parent->right; // 获取叔父节点
            // 当叔父节点存在且为红色时，进行情况1的处理
            if (y != NULL && y->color == RED) {
                z->parent->color = BLACK; // 将父节点设为黑色
                y->color = BLACK; // 将叔父节点设为黑色
                z->parent->parent->color = RED; // 将祖父节点设为红色
                z = z->parent->parent; // 将 z 移动到祖父节点处
            } else {
                // 当叔父节点不存在或为黑色时，进行情况2的处理
                if (z == z->parent->right) { // 如果 z 是父节点的右子节点
                    z = z->parent; // 将 z 移动到父节点处
                    rotateLeft(root, z); // 左旋转
                }
                z->parent->color = BLACK; // 将父节点设为黑色
                z->parent->parent->color = RED; // 将祖父节点设为红色
                rotateRight(root, z->parent->parent); // 右旋转
            }
        } else { // 当父节点是祖父节点的右子节点时，与上述情况对称
            Node *y = z->parent->parent->left;
            if (y != NULL && y->color == RED) {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;
                z = z->parent->parent;
            } else {
                if (z == z->parent->left) {
                    z = z->parent;
                    rotateRight(root, z);
                }
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                rotateLeft(root, z->parent->parent);
            }
        }
    }
    (*root)->color = BLACK; // 将根节点设为黑色
}

// 插入新节点到红黑树中
void insert(Node **root, int data) {
    Node *newNode = createNode(data); // 创建新节点
    Node *parent = NULL;
    Node *current = *root;
    while (current != NULL) { // 寻找插入位置
        parent = current;
        if (newNode->data < current->data)
            current = current->left;
        else
            current = current->right;
    }
    newNode->parent = parent; // 设置新节点的父节点
    if (parent == NULL)
        *root = newNode; // 如果树为空，则将新节点设为根节点
    else if (newNode->data < parent->data)
        parent->left = newNode; // 如果新节点值小于父节点值，则设为左子节点
    else
        parent->right = newNode; // 否则设为右子节点
    fixViolation(root, newNode); // 修正插入可能导致的红黑树性质违反
}

// 在红黑树中查找指定值的节点
Node* search(Node *root, int data) {
    while (root != NULL) {
        if (data < root->data)
            root = root->left; // 在左子树中查找
        else if (data > root->data)
            root = root->right; // 在右子树中查找
        else
            return root; // 找到节点
    }
    return NULL; // 未找到节点
}

// 寻找以给定节点为根的子树中的最小值节点
Node* minValueNode(Node* node) {
    Node* current = node;
    while (current->left != NULL)
        current = current->left; // 不断向左遍历直到最左叶节点
    return current; // 返回最小值节点
}

// 修正双黑节点情况
void fixDoubleBlack(Node **root, Node *x) {
    if (x == *root) // 如果 x 是根节点，直接返回
        return;
    Node *sibling = NULL; // 声明一个指向兄弟节点的指针
    while (x != *root && x->color == BLACK) { // 当 x 不是根节点且颜色为黑色时执行循环
        if (x == x->parent->left) { // 如果 x 是父节点的左子节点
            sibling = x->parent->right; // 获取兄弟节点
            if (sibling->color == RED) { // 如果兄弟节点为红色
                sibling->color = BLACK; // 将兄弟节点设为黑色
                x->parent->color = RED; // 将父节点设为红色
                rotateLeft(root, x->parent); // 左旋转
                sibling = x->parent->right; // 更新兄弟节点
            }
            if (sibling->left->color == BLACK && sibling->right->color == BLACK) { // 如果兄弟节点的两个子节点都为黑色
                sibling->color = RED; // 将兄弟节点设为红色
                x = x->parent; // 将 x 移动到父节点处
            } else {
                if (sibling->right->color == BLACK) { // 如果兄弟节点的右子节点为黑色
                    sibling->left->color = BLACK; // 将兄弟节点的左子节点设为黑色
                    sibling->color = RED; // 将兄弟节点设为红色
                    rotateRight(root, sibling); // 右旋转
                    sibling = x->parent->right; // 更新兄弟节点
                }
                sibling->color = x->parent->color; // 将兄弟节点的颜色设为父节点的颜色
                x->parent->color = BLACK; // 将父节点设为黑色
                sibling->right->color = BLACK; // 将兄弟节点的右子节点设为黑色
                rotateLeft(root, x->parent); // 左旋转
                x = *root; // 将 x 设为根节点
            }
        } else { // 如果 x 是父节点的右子节点，与上述情况对称
            sibling = x->parent->left;
            if (sibling->color == RED) {
                sibling->color = BLACK;
                x->parent->color = RED;
                rotateRight(root, x->parent);
                sibling = x->parent->left;
            }
            if (sibling->right->color == BLACK && sibling->left->color == BLACK) {
                sibling->color = RED;
                x = x->parent;
            } else {
                if (sibling->left->color == BLACK) {
                    sibling->right->color = BLACK;
                    sibling->color = RED;
                    rotateLeft(root, sibling);
                    sibling = x->parent->left;
                }
                sibling->color = x->parent->color;
                x->parent->color = BLACK;
                sibling->left->color = BLACK;
                rotateRight(root, x->parent);
                x = *root;
            }
        }
    }
    x->color = BLACK; // 将最终 x 设为黑色
}

// 替换节点
void transplant(Node **root, Node *u, Node *v) {
    if (u->parent == NULL) // 如果 u 是根节点
        *root = v; // 将根节点设为 v
    else if (u == u->parent->left) // 如果 u 是其父节点的左子节点
        u->parent->left = v; // 将 v 设为其父节点的左子节点
    else // 如果 u 是其父节点的右子节点
        u->parent->right = v; // 将 v 设为其父节点的右子节点
    if (v != NULL) // 如果 v 不为空
        v->parent = u->parent; // 将 v 的父节点设为 u 的父节点
}


// 删除节点函数
void deleteNode(Node **root, int data) {
    Node *z = search(*root, data); // 在树中查找值为 data 的节点
    if (z == NULL) { // 如果未找到节点
        printf("Node with value %d not found\n", data); // 输出未找到节点的信息
        return; // 返回
    }
    Node *y = z; // 将 y 设为 z
    Node *x; // 声明一个指向后继节点的指针 x
    int yOriginalColor = y->color; // 保存 y 的颜色
    if (z->left == NULL) { // 如果 z 的左子节点为空
        x = z->right; // 将 x 设为 z 的右子节点
        transplant(root, z, z->right); // 将 z 替换为其右子节点
    } else if (z->right == NULL) { // 如果 z 的右子节点为空
        x = z->left; // 将 x 设为 z 的左子节点
        transplant(root, z, z->left); // 将 z 替换为其左子节点
    } else { // 如果 z 既有左子节点又有右子节点
        y = minValueNode(z->right); // 找到 z 的右子树中的最小值节点 y
        yOriginalColor = y->color; // 保存 y 的颜色
        x = y->right; // 将 x 设为 y 的右子节点
        if (y->parent == z) // 如果 y 是 z 的直接子节点
            x->parent = y; // 将 x 的父节点设为 y
        else {
            transplant(root, y, y->right); // 将 y 替换为其右子节点
            y->right = z->right; // 将 y 的右子节点设为 z 的右子节点
            y->right->parent = y; // 更新 y 的右子节点的父节点
        }
        transplant(root, z, y); // 将 z 替换为 y
        y->left = z->left; // 将 y 的左子节点设为 z 的左子节点
        y->left->parent = y; // 更新 y 的左子节点的父节点
        y->color = z->color; // 将 y 的颜色设为 z 的颜色
    }
    if (yOriginalColor == BLACK) // 如果 y 的原始颜色为黑色
        fixDoubleBlack(root, x); // 修正双黑节点情况
    free(z); // 释放删除的节点的内存
}

// 中序遍历函数
void inorder(Node *root) {
    if (root == NULL) // 如果根节点为空
        return; // 返回
    inorder(root->left); // 递归遍历左子树
    printf("%d ", root->data); // 输出当前节点的值
    inorder(root->right); // 递归遍历右子树
}


int main() {
    Node *root = NULL;
    insert(&root, 7);
    insert(&root, 3);
    insert(&root, 18);
    insert(&root, 10);
    insert(&root, 22);
    insert(&root, 8);
    insert(&root, 11);
    insert(&root, 26);
    insert(&root, 2);
    insert(&root, 6);
    insert(&root, 13);

    printf("Inorder traversal of the tree: ");
    inorder(root);
    printf("\n");

    deleteNode(&root, 18);
    printf("Inorder traversal after deletion of 18: ");
    inorder(root);
    printf("\n");

    int searchData = 10;
    Node *searchResult = search(root, searchData);
    if (searchResult != NULL)
        printf("%d found in the tree.\n", searchData);
    else
        printf("%d not found in the tree.\n", searchData);

    int searchData2 = 18;
    Node *searchResult2 = search(root, searchData2);
    if (searchResult2 != NULL)
        printf("%d found in the tree.\n", searchData2);
    else
        printf("%d not found in the tree.\n", searchData2);

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1676470.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Kimi智能助手：你的全天候AI伙伴

Kimi智能助手：你的全天候AI伙伴

Kimi使用链接&#xff1a; https://kimi.moonshot.cn/ Kimi手机端下载链接&#xff1a; https://kimi.moonshot.cn/download/app?refchat 简介&#xff1a; Kimi AI 是由月之暗面科技有限公司&#xff08;Moonshot AI&#xff09;开发的一款人工智能助手&#xff0c;它具备多…
阅读更多...
正运动技术与合作伙伴邀您共聚2024武汉光博会

正运动技术与合作伙伴邀您共聚2024武汉光博会

■展会名称&#xff1a; 2024“中国光谷”光电子博览会暨论坛&#xff08;以下简称“武汉光博会”&#xff09; ■展会日期 2024年5月16日 - 18日 ■展馆地点 中国光谷科技会展中心A3馆 ■展位号 3A21 5月16至18日&#xff0c;中国光谷科技会展中心将举办第二十届武汉光…
阅读更多...
nmap使用教程

nmap使用教程

nmap使用教程 一、nmap简介二、nmap常用命令2.1、target specification&#xff08;目标规范&#xff09;2.1.1、用法2.1.2、详情 2.2、HOST DISCOVERY&#xff08;主机发现&#xff09;2.2.1、用法2.2.2、详情 2.3、SCAN TECHNIQUES&#xff08;扫描技术&#xff09;2.4、PORT…
阅读更多...
【Web】HNCTF 2024 题解(部分)

【Web】HNCTF 2024 题解(部分)

目录 Please_RCE_Me ezFlask GoJava ez_tp GPTS Please_RCE_Me <?php if($_GET[moran] flag){highlight_file(__FILE__);if(isset($_POST[task])&&isset($_POST[flag])){$str1 $_POST[task];$str2 $_POST[flag];if(preg_match(/system|eval|assert|call|…
阅读更多...
从零开始开发企业培训APP：在线教育系统源码剖析

从零开始开发企业培训APP：在线教育系统源码剖析

今天&#xff0c;小编将深入剖析企业培训APP的开发&#xff0c;从零开始为企业构建一个高效、实用的在线教育系统。 一、需求分析 1.主要功能需求 包括但不限于&#xff1a; -用户管理 -课程管理 -学习计划 -互动功能 -考核评估 -统计分析 二、技术选型 1.前端技术 …
阅读更多...
PG数据文件和块管理与Oracle比较

PG数据文件和块管理与Oracle比较

之前有说过PG数据库中的对象oid与数据文件一一对应&#xff0c;创建的数据库如果没有指定表空间&#xff0c;则会默认放在默认表空间中&#xff0c;例如&#xff1a; 1.对象OID与数据文件对应关系 Oracle的逻辑与物理对应关系如下&#xff1a; 两种结果相比较而言&#xff1a; …
阅读更多...
拯救者杯OPENAIGC开发者大赛城市巡回沙龙，苏州站报名开启！

拯救者杯OPENAIGC开发者大赛城市巡回沙龙，苏州站报名开启！

由联想拯救者、AIGC开放社区、英特尔联合主办的“AI生成未来第二届拯救者杯OPENAIGC开发者大赛”自上线以来&#xff0c;吸引了广大开发者的热情参与。 为了向技术开发者、业务人员、高校学生、以及个体创业人员等参赛者们提供更充分的帮助与支持&#xff0c;AIGC开放社区特别…
阅读更多...
RockChip Android8.1 EthernetService分析

RockChip Android8.1 EthernetService分析

一：概述 本篇文章将围绕RK Android8.1 SDK对Ethernet做一次框架分析，包含Framework层和APP层。 当前版本SDK默认只支持一路Ethernet，熟悉Ethernet工作流程后通过修改最终会在系统Setting以太网中呈现多路选项（可以有多种实现方式），博主通过增加ListPreference实现的效果…
阅读更多...
C++设计模式|创建型 5.原型模式

C++设计模式|创建型 5.原型模式

1.什么是原型模式&#xff1f; 原型模式⼀种创建型设计模式&#xff0c;该模式的核⼼思想是基于现有的对象创建新的对象&#xff0c;⽽不是从头开始创建。 在原型模式中&#xff0c;通常有⼀个原型对象&#xff0c;它被⽤作创建新对象的模板。新对象通过复制原型对象的属性和状…
阅读更多...
namenode启动失败 org.apache.hadoop.hdfs.server.common.InconsistentFSStateException:

namenode启动失败 org.apache.hadoop.hdfs.server.common.InconsistentFSStateException:

小白的Hadoop学习笔记 2024/5/14 18:26 文章目录 问题解决报错浅浅分析一下core-ste.xml 问题 namenode启动失败 读日志 安装目录下 vim /usr/local/hadoop/logs/hadoop-tangseng-namenode-hadoop102.log2024-05-14 00:22:46,262 ERROR org.apache.hadoop.hdfs.server.namen…
阅读更多...
开源可视化表单服务商：提升自主研发 助力流程化办公！

开源可视化表单服务商：提升自主研发 助力流程化办公！

当前&#xff0c;做好流程化办公可以为企业实现提质增效的办公效果&#xff0c;助力企业进入数字化转型。作为开源可视化表单服务商&#xff0c;流辰信息坚持研发创新理念&#xff0c;努力提升自主研发能力&#xff0c;专为广大客户朋友提供集产品、框架定制、产品交付为一体的…
阅读更多...
Java面试八股之Java中有哪些原子类，原理是什么

Java面试八股之Java中有哪些原子类，原理是什么

Java中有哪些原子类&#xff0c;原理是什么 AtomicInteger 和 AtomicLong&#xff1a; 用于对整数&#xff08;int&#xff09;和长整数&#xff08;long&#xff09;进行原子操作。 原理&#xff1a;它们内部封装了一个整型或长整型变量&#xff0c;并通过使用Unsafe类提供…
阅读更多...
查找总价格为目标值的两个商品（双指针）

查找总价格为目标值的两个商品（双指针）

算法原理&#xff1a; 其实我们首先想到的方法肯定是暴力&#xff0c;两个for循环嵌套就能找到&#xff0c;但肯定会超时。 其实啊一切算法的总结都是在暴力的基础上进行的&#xff0c;算法其实就是对暴力进一步的优化。 定义两个指针&#xff0c;分别指向两端&#xff0c;然后…
阅读更多...
单用户模式破解root密码

单用户模式破解root密码

目录 一. 破解root密码 1. 查看操作系统版本 2.重启系统&#xff0c;进入grub菜单&#xff0c;选择要使用的内核&#xff0c;按e进入​编辑 3. 找到linux16那一行&#xff0c;把光标移动到最后&#xff0c;添加 init/bin/sh 然后ctrlx保存退出会自动进入系统 4. 进入系统后…
阅读更多...
程序员就是管道工

程序员就是管道工

程序是由指令和数据组成的。 指令是按照特定的顺序执行的&#xff0c;这些顺序好比水的流向。 要想让水高效地流向我们想要的地方&#xff0c;就要设计一个精良的管道系统&#xff0c;这好比算法。 剩下的就是修建管道了&#xff0c;你要知道各种管的型号、用途&#xff0c;然…
阅读更多...
Java 包语句，看这一篇就够了

Java 包语句，看这一篇就够了

1.设计的文件层级 我们将“Package”文件夹称为根目录&#xff0c;“Level01”称为一级目录&#xff0c;“Level02”称为二级目录&#xff0c;以此类推。 2.发现在不同目录下的包名有如下特征&#xff1a; 根目录下的文件不需要包名&#xff0c;可以理解成包名为 “”一级目录…
阅读更多...
洁太司检测试剂盒：肝癌早诊新利器，共筑健康未来

洁太司检测试剂盒：肝癌早诊新利器，共筑健康未来

随着科技进步及医疗技术的不断创新&#xff0c;人类对疾病的早期诊断和治疗提出了更高的要求。 先思达生物近期推出的“洁太司-寡糖链检测试剂盒”&#xff0c;在原发性肝细胞癌的诊断领域实现了重大突破&#xff0c;获得了国家药品监督管理局&#xff08;NMPA&#xff09;的三…
阅读更多...
8.基于鱼鹰优化算法(OOA)优化VMD参数(OOA-VMD)

8.基于鱼鹰优化算法(OOA)优化VMD参数(OOA-VMD)

代码原理 鱼鹰优化算法&#xff08;Osprey Optimization Algorithm, OOA&#xff09;是一种基于仿生学原理的启发式优化算法&#xff0c;它模拟了鱼鹰觅食的行为&#xff0c;通过调整搜索空间中的个体位置来优化目标函数。 鱼鹰优化算法可参考&#xff1a;鱼鹰优化算法(Ospre…
阅读更多...
【系统运维】如何查找用户账号锁定位置

【系统运维】如何查找用户账号锁定位置

【问题】AD环境下&#xff0c;经常会遇到用户账号因输错密码次数超限而被锁的情况。 如果AD环境较简单还好说&#xff0c;但如果域控很多&#xff0c;要定位用户账号被锁在哪里就有点小麻烦了&#xff0c;比如开发人员可能会频繁登录多台服务器&#xff0c;如果某台服务器缓存了…
阅读更多...
【Android Studio】使用UI工具绘制，ConstraintLayout 限制性布局，快速上手

【Android Studio】使用UI工具绘制，ConstraintLayout 限制性布局，快速上手

文章目录 一、前言二、绘制效果三、ConstraintLayout 使用方法3.1 创建布局文件3.2 替换配置3.3 设置约束&#xff0c;步骤13.4 设置约束&#xff0c;步骤23.5 其他设置 四、结束 一、前言 在进行Android APP开发过程中&#xff0c;减少layout嵌套即可改善UI的绘制性能&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023